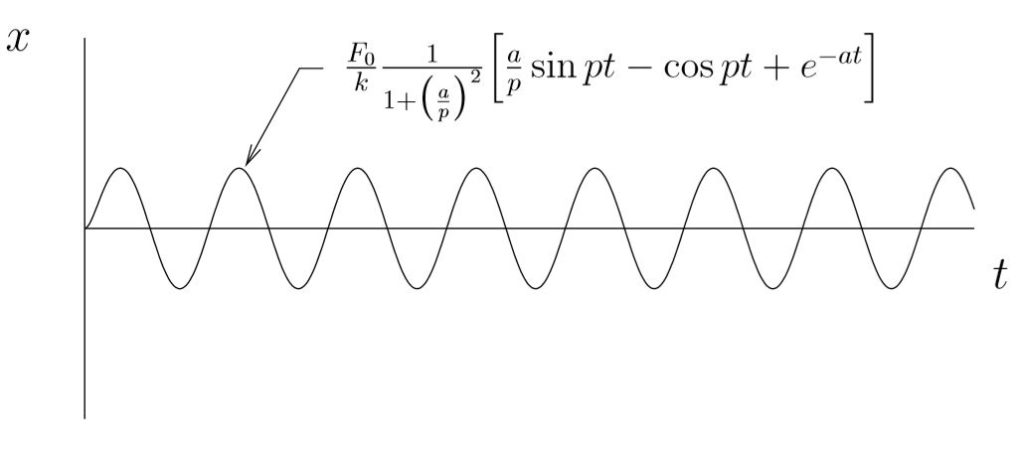
Transient Vibrations: Response of Spring–Mass System to an Exponential Decay
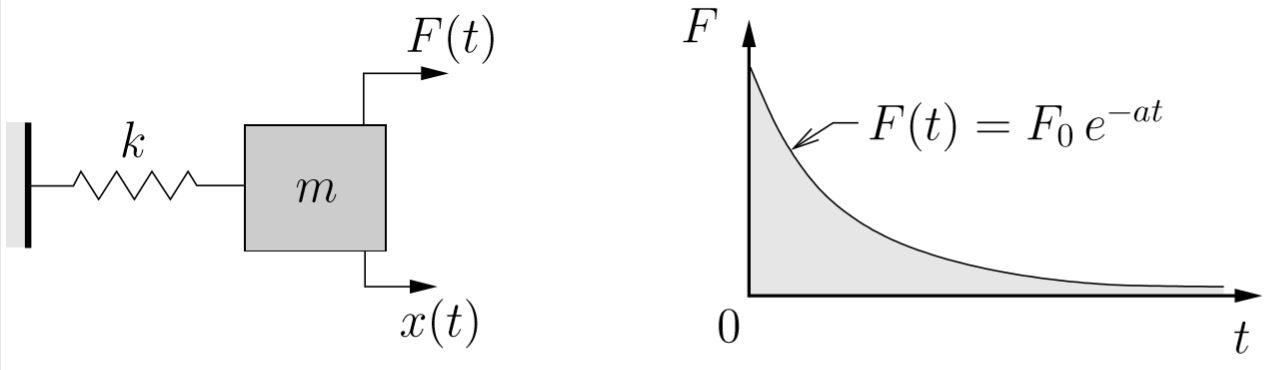
The equation of motion in this case is
![]()
for which the particular solution can be shown to be
![]()
so that the total solution becomes
(7.7) ![]()
If the initial conditions are
![]()
then
![]()
and we get
(7.8) ![]()
or
![Rendered by QuickLaTeX.com \begin{equation*}\boxed{x(t) = \frac{F_0}{k} \frac{1}{1 + \bigl( \frac{a}{p}\bigr)^2}\biggl[\frac{a}{p} \sin{pt} - \cos{pt} + e^{-at} \biggr]}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c3fd7f87ae4a632c88150dda765e228f_l3.png)
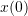 =
= 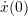 = 0
= 0