Approximate Methods for Multiple Degree of Freedom Systems: Kinetic and Potential Energies in Multiple Degree of Freedom in Systems
So far we have considered multiple degree of freedom systems and have shown how to find the natural frequencies and modes shapes associated with such systems, which is essentially an eigenvalue problem. Often we are only interested in the lowest (or possibly the largest) natural frequency in a system. There are methods that can be used to estimate these frequencies which do not entail finding all of the natural frequencies of a system. We will discuss two such methods in this section, Rayleigh’s Quotient and Dunkerley’s Formula. To begin with, however, we need to consider how we can represent kinetic and potential energies in multiple degree of freedom systems.
Consider an ![]() degree of freedom system with
degree of freedom system with ![]() coordinates
coordinates ![]() describing some displaced configuration of the system. Each
describing some displaced configuration of the system. Each ![]() may be a linear or angular displacement. Let
may be a linear or angular displacement. Let
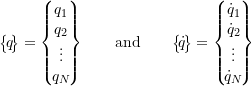
represent the values of the coordinates and their associated derivatives. For the linear systems considered here it can be shown that the potential energy in the system is given by
(9.1) ![]()
where ![]() is the stiffness matrix discussed earlier. Note that the potential energy is therefore zero at the equilibrium position. Similarly, the kinetic energy is given by
is the stiffness matrix discussed earlier. Note that the potential energy is therefore zero at the equilibrium position. Similarly, the kinetic energy is given by
(9.2) ![]()
where ![]() is the mass matrix.
is the mass matrix.
EXAMPLE
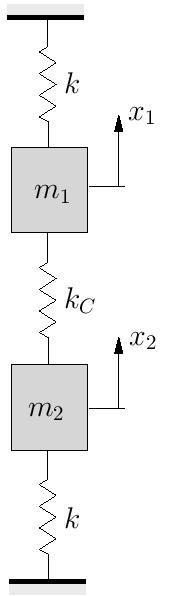
At some instant in time, the masses in the system shown below are in positions ![]() and
and ![]() and have velocities
and have velocities ![]() and
and ![]() , respectively.
, respectively.

![Rendered by QuickLaTeX.com \[\begin{split}U &= \frac{1}{2}\left\{q\right\}^T\left[k\right]\left\{q\right\} \\T &= \frac{1}{2}\left\{\dot{q}\right\}^T\left[m\right]\left\{\dot{q}\right\}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9658c791b5c93ea09a1a62f0837837c6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\left[k\right] &= \begin{bmatrix} k+ k_C & -k_C\\ -k_C & k+k_C \end{bmatrix}\\\left[m\right] &= \begin{bmatrix} m_1 & 0\\ 0 & m_2 \end{bmatrix}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8b988b0c0e7fee1a32c7216e4973c4ec_l3.png)