Open Educational Resources

Forced Vibrations of Damped Single Degree of Freedom Systems: Base Excitation in a Damped System


We can also consider the response of a damped spring–mass system subjected to base excitation. Among other applications, these results are useful when considering the operation of transducers that measure vibrations.

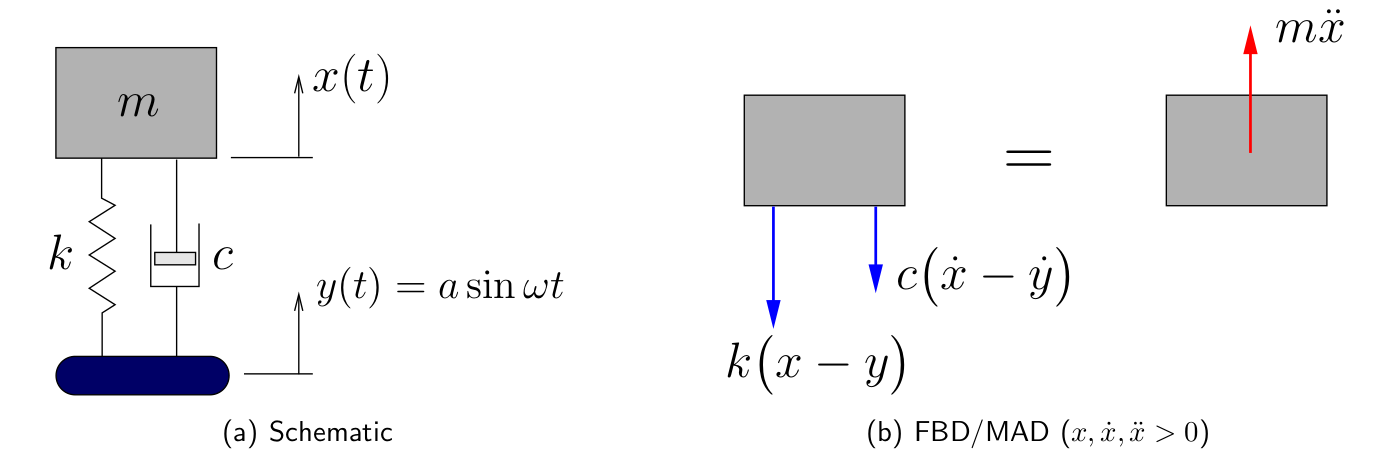
Figure 5.11: Damped spring–mass system subjected to harmonic forcing function

Figure 5.11(a) illustrates such a situation schematically while Figure 5.11(b) shows the corresponding FBD/MAD diagram. Applying Newton’s Laws we find

(5.23) 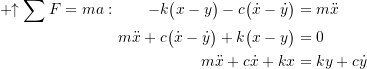  \begin{align*} +\!\!\uparrow\sum F = ma:\qquad -k\bigl(x-y\bigr) -c\bigl(\dot{x}-\dot{y}\bigr) &= m \ddot{x} \nonumber \\ \label{eq:DampedBaseExcitationEOMI} m \ddot{x} + c\bigl(\dot{x}-\dot{y}\bigr) + k\bigl(x-y\bigr) &= 0 \\ m \ddot{x} + c \dot{x} + k x &= ky + c \dot{y} \nonumber \end{align*}

or since y=a\sin \omega t

(5.24)   \[m \ddot{x} + c\dot{x} +k x = k a \sin \omega t + c a \omega \cos \omega t\]

This can also be expressed as

    \[m \ddot{x} + c\dot{x} +kx = \ensuremath{\mathbb{R}} \sin{(\omega t - \alpha)}\]

where

    \[\ensuremath{\mathbb{R}} = a \sqrt{k^2 + \bigl(c \omega\bigr)^2}, \qquad\alpha = \tan^{-1}{\biggl[\frac{-c \omega}{k}\biggr]}\]


As a result, we can see that the base excitation is equivalent to applying a harmonic force of magnitude \ensuremath{\mathbb{R}} to a mass with a fixed base. We have previously found the steady state solution for such a case (equations (5.7) and (5.9)) which here becomes


    \[x(t) = \frac{a \sqrt{k^2 + \bigl(c \omega\bigr)^2}}{\ensuremath{\sqrt{(k-m\omega)^2 + (c\omega)^2}}}\sin{(\omega t - \alpha -\phi_1)}\]


where

    \[\phi_1 = \tan^{-1}{\Biggl[\frac{c \omega}{k-m\omega^2}\Biggr]}\]

Therefore we could write the response as

    \[x(t) = \mathbb{X} \sin{(\omega t - \Phi)}\]


where

    \[\frac{\mathbb{X}}{a} = \frac{\sqrt{k^2 + \bigl(c \omega\bigr)^2}}{\ensuremath{\sqrt{(k-m\omega)^2 + (c\omega)^2}}}\]


and

    \[\Phi = \alpha + \phi_1 =\tan^{-1}{\biggl[\frac{-c \omega}{k}\biggr]} +\tan^{-1}{\biggl[\frac{c \omega}{k-m\omega^2}\biggr]}\]

However, this in often not the most convenient form for the phase angle. It can be shown (after some algebra) that

    \[\tan \Phi = \frac{m c \omega^3}{k\bigl(k-m\omega^2\bigr)+\bigl(c \omega\bigr)^2 }\]


which can also be expressed in non-dimensional form as

    \[\tan \Phi = \frac{2 \zeta \left(\ensuremath{\frac{\omega}{\ensuremath{p}}}\right)^3}{1 + \bigl(4\zeta^2-1\bigr)\left(\ensuremath{\frac{\omega}{\ensuremath{p}}}\right)^2}\]

To summarize, the response of the damped spring–mass system to harmonic base excitation is given by

(5.25)   \[x(t) = \mathbb{X} \sin{(\omega t - \Phi)}\]


where

(5.26)   \[\frac{\mathbb{X}}{a} = \frac{\sqrt{k^2 + \bigl(c \omega\bigr)^2}}{\ensuremath{\sqrt{(k-m\omega)^2 + (c\omega)^2}}}\]


and

(5.27)   \[\Phi = \tan^{-1} \Biggl[\frac{m c \omega^3}{k\bigl(k-m\omega^2\bigr)+\bigl(c \omega\bigr)^2 } \Biggr]\]

In dimensionless form these become

(5.28)   \[\boxed{ \frac{\mathbb{X}}{a} = \frac{\sqrt{1 + \bigl(2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \bigr)^2}}{\ensuremath{\sqrt{\left[1-\left(\ensuremath{\frac{\omega}{\ensuremath{p}}}\right)^2\right]^2 + \left[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \right]^2}}}}\]


and

(5.29)   \[\boxed{ \Phi = \tan^{-1} \Biggl[\frac{2 \zeta \left(\ensuremath{\frac{\omega}{\ensuremath{p}}}\right)^3}{1 + \bigl(4\zeta^2-1\bigr)\left(\ensuremath{\frac{\omega}{\ensuremath{p}}}\right)^2}\Biggr]}\]

Figure 5.12: Response amplitude of damped spring–mass system subjected to harmonic base excitation

The term \frac{\mathbb{X}}{a} can be thought of as the dynamic magnification factor in this situation as it represents the ratio of the amplitude of the motion of the mass to the amplitude of motion of the base.

Figure 5.12 illustrates this relationship. We can see that this factor is exactly the same as the transmissibility for the forced damped situation considered previously (equation (5.19) and Figure 5.7). Therefore the problem of isolating a mass from the motion of the base is essentially the same problem as preventing a disturbing force acting on the mass from being transmitted to the supporting structure (the base).

EXAMPLE

An instrument package of mass m is to be isolated from a vibrating surface which is moving with an amplitude Y at a frequency of 600 RPM.

This image has an empty alt attribute; its file name is 5ex4.png

(a) What should the natural frequency of the system be if the maximum amplitude of the instrument package is to be \frac{1}{8} of Y?

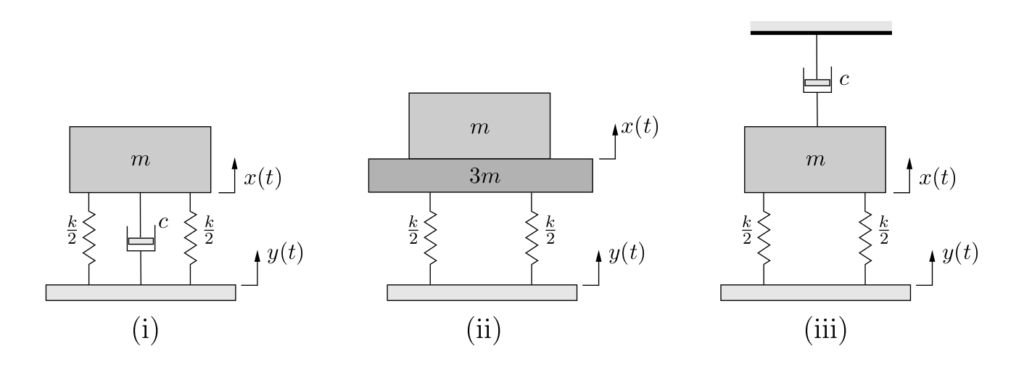
(b) In order to reduce the amplitude of oscillation even further, several ideas (illustrated below) are proposed to improve the situation. Evaluate each of these ideas and determine if it will improve or worsen the situation. Use a combination of calculations and diagrams to support your reasoning.
(i) A damper is added between the mass and vibrating surface which provides a damping ratio of \zeta = 1.0
(ii) An inertia mass equal to 3m is added on the same supports.
(iii) A damper is added between the instrument package and a fixed support to provide a damping ratio of \zeta = 1.0. (Note: start from the differential equation of motion.)

This image has an empty alt attribute; its file name is 5ex5-1024x375.png

EXAMPLE

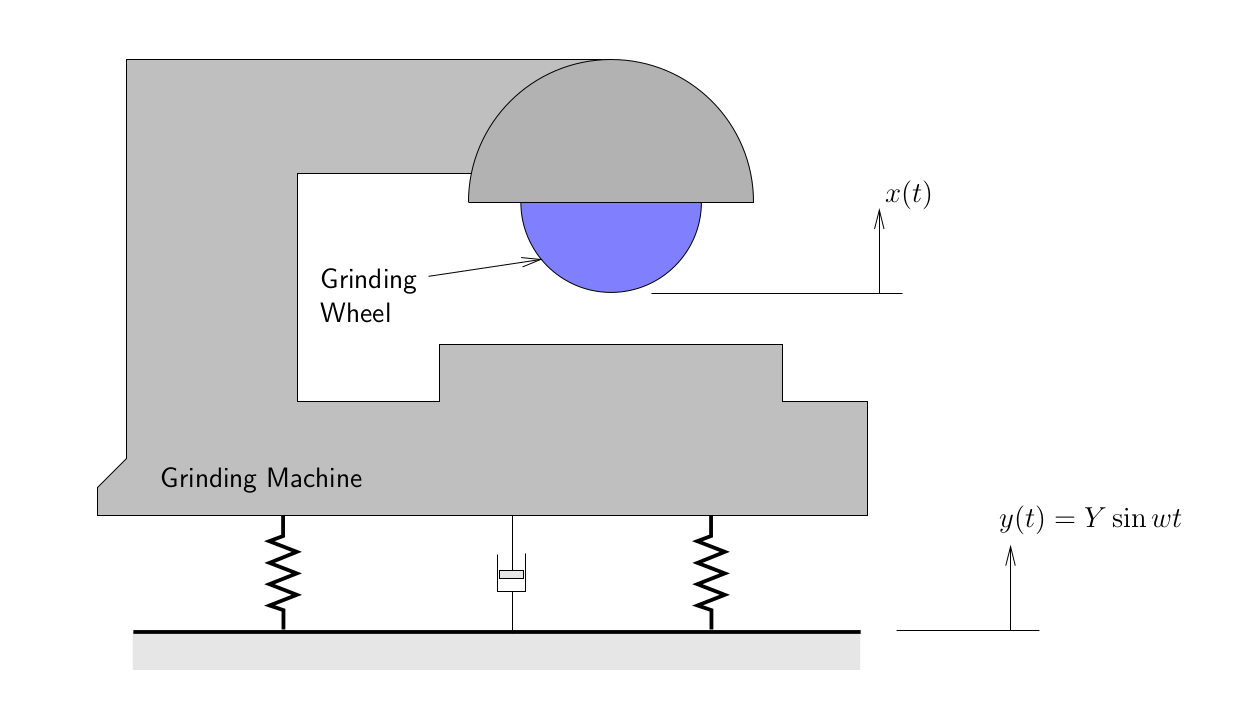
A precision grinding machine is supported on an isolator that has a stiffness of 1 MN/m and a viscous damping constant of 1 kN·s/m. The floor on which the machine is mounted is subjected to a harmonic disturbing force due to the operation of a unbalanced engine in the vicinity of the grinding machine operating at a speed of 6000 RPM. Determine the maximum acceptable amplitude of the floor motion (Y) if the resulting amplitude of vibration of the grinding wheel is restricted to be 10^{−6} m. Assume that the grinding machine and the wheel are a rigid body of weight 5000 N.

This image has an empty alt attribute; its file name is 5ex6.png

Relative Motion Between the Mass and the Base

In the previous section we considered the response of a damped spring–mass system subjected to harmonic base excitation and found the absolute response of the mass. Those results are not always the most convenient to use. For example, in many vibration measurement instruments we usually directly measure only the relative motion between the mass and the base and then try to use this measurement to infer the underlying motion of the base (which is typically what we would be trying to measure).

Considering Figure 5.11(a) once again, the relative motion z between the mass and the base
is given by

    \[z(t) = x(t)-y(t).\]

However, as we have seen previously there is a phase difference \Phi between x(t) and y(t), given by equation (5.29), which must be taken into account. For example we could take our previous solutions and expand them using trigonometric identities to account for this phase difference. An alternative (and often easier) approach is to consider the relative motion directly.

Since

    \[z = x - y\]


we can write

    \begin{align*}\dot{z} &= \dot{x} - \dot{y}, \\\ddot{z} &= \ddot{x} - \ddot{y} \qquad\text{or}\qquad \ddot{x} = \ddot{z} + \ddot{y}\end{align*}



The original equation of motion in (5.23)

    \[m \ddot{x} + c\bigl(\dot{x}-\dot{y}\bigr) + k\bigl(x-y\bigr) = 0\]


can then be written as

    \begin{align*} m \Bigl[ \ddot{z} + \ddot{y} \Bigr] + c \dot{z} + k z &= 0, \\ m \ddot{z} + c \dot{z} + k z &= -m \ddot{y}. \end{align*}

However, since y=a\sin \omega t, \ddot{y}= -a \omega^2 \sin \omega t so the equation of motion becomes

(5.30)   \[m \ddot{z} + c \dot{z} + k z = \underbrace{m a \omega^2\rule[-1mm]{0pt}{0pt}}_{\text F_0} \sin \omega t\]

We note that this equation is identical to that obtained for the forced vibration situation (and particularly the case of a rotating imbalance) which we have already considered. The solution to this equation is therefore

(5.31)   \[z(t) = \mathbb{Z} \sin (\omega t - \phi)\]


where

(5.32)   \[\mathbb{Z} = \frac{\dfrac{m a \omega^2}{k}}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}} = \frac{a \left(\ensuremath{\dfrac{\omega}{\ensuremath{p}}}\right)^2}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}\]


and

(5.33)   \[\phi = \tan^{-1} \Biggl[\frac{2\zeta\ensuremath{\frac{\omega}{\ensuremath{p}}}}{\ensuremath{1-\bigl(\ensuremath{\frac{\omega}{\ensuremath{p}}}\bigr)^2}} \Biggr].\]


Equation (5.32) can be rearranged as

(5.34)   \[\boxed{ \frac{\mathbb{Z}}{a} = \frac{\left(\ensuremath{\dfrac{\omega}{\ensuremath{p}}}\right)^2}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}}\]

which determines the ratio of the amplitude of the relative motion to that of the base motion itself. This relationship is shown in Figure 5.13. (This is the same relationship found for the ratio \frac{M\mathbb{X}}{\ensuremath{\tilde{m}} e} in Equation (5.22) and Figure 5.10). Note again that as \zeta\rightarrow0 this gives us the same results as in the undamped case.

We can apply these results to the use of a variety of vibration measurement instruments.

Figure 5.13: Amplitude of the relative motion for a damped spring–mass system subjected to harmonic base excitation
Vibrometer or Seismometer

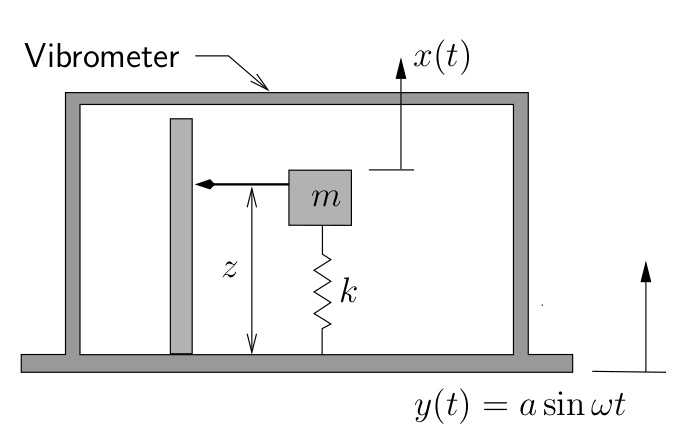
These instruments tend to be large and have soft springs so that their natural frequencies are small. As a result they are usually used in the range where \ensuremath{\frac{\omega}{\ensuremath{p}}} is large (\ensuremath{\frac{\omega}{\ensuremath{p}}}\gg 1). In this range, we can see from Figure 5.13 that as \zeta\rightarrow0,

    \[\frac{\mathbb{Z}}{a} \longrightarrow 1\]

so that the amplitude of the relative motion \mathbb{Z} between the mass and the base is the same as the amplitude a of the actual motion of the base. In operation, the mass remains approximately stationary while the base moves with the supporting structure (whose vibrations are being measured).

These devices tend to have little damping, but as can be seen from Figure 5.13, even moderate
amounts of damping have only a small effect in this region.

Accelerometer

Accelerometers are widely used to measure acceleration levels. They tend to be small and stiff and as a result usually have very high natural frequencies. They are useful for measuring vibrations at frequencies that are much smaller than their own natural frequency (\ensuremath{\frac{\omega}{\ensuremath{p}}} \ll 1).
We can see from equation 5.34 that as \ensuremath{\frac{\omega}{\ensuremath{p}}} approaches zero,

    \[\frac{\mathbb{Z}}{a} \longrightarrow \left(\ensuremath{\dfrac{\omega}{\ensuremath{p}}}\right)^2 \qquad\text{or}\qquad\mathbb{Z} \simeq \frac{1}{\ensuremath{p}^2} (a \omega^2)\]

where a\omega^2 is the magnitude of the acceleration of the base. Therefore, in this region the amplitude of the relative motion is approximately proportional to the magnitude of the acceleration of the base.

To understand the response better, note that equation (5.34) could be rearranged as

    \[\mathbb{Z} = \frac{1}{\ensuremath{p}^2 } \bigl( a \omega^2 \bigr)\underbrace{\frac{1}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}}_{\text{\small Factor } \approx 1}\]

where \ensuremath{p}^2 is a constant for the accelerometer that is usually determined by calibration.
As can be seen, the value of the factor

    \[\frac{1}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}\]

approaches 1 as \ensuremath{\frac{\omega}{\ensuremath{p}}} \rightarrow0 but for \ensuremath{\frac{\omega}{\ensuremath{p}}} \neq 0 this factor is different from one and this difference contributes to the error in the measurement.

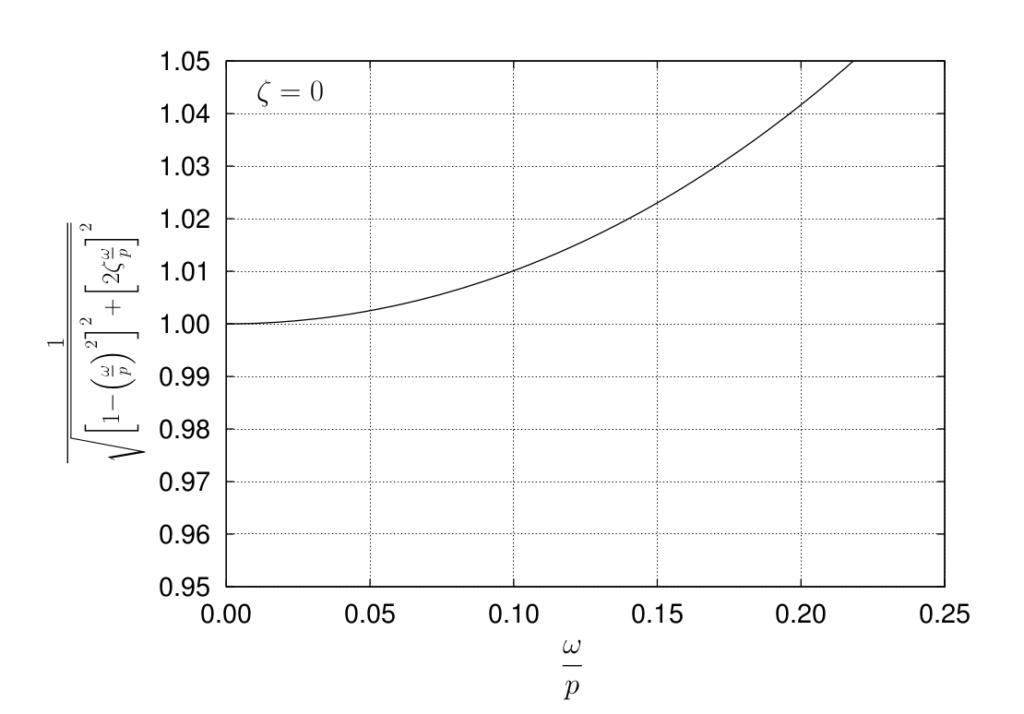
To see this effect, figure 5.14 illustrates this region of the response for an undamped accelerometer. For a frequency ratio \ensuremath{\frac{\omega}{\ensuremath{p}}} \approx 0.1, the value of the factor is approximately 1.01, which corresponds to approximately a 1\% error. At a frequency ratio \ensuremath{\frac{\omega}{\ensuremath{p}}} \approx 0.2, the value of the factor increases to approximately 1.04, which corresponds to a 4\% error. Further increases in \ensuremath{\frac{\omega}{\ensuremath{p}}} lead to rapidly increasing errors.

Figure 5.14: Accelerometer response for small \frac{\omega}{p} ratios
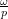Figure 5.15: Accelerometer response for small \frac{\omega}{p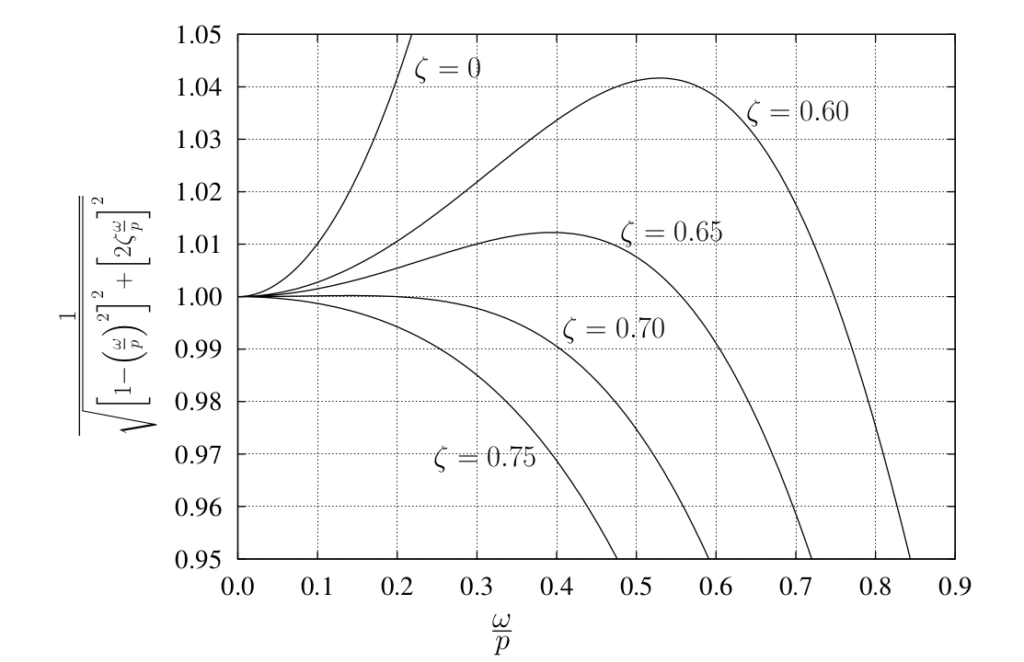} ratios

We can take advantage of damping to improve this behaviour. Figure 5.15 shows the effect of damping on the response. As shown in this figure, for damping ratios between about 0.65 and 0.7 this factor remains much closer to one over a wider range of frequency ratios. For example, with \zeta\approx 0.7, the error introduced by assuming this factor to be unity is less than 1\% over a frequency range of 0 < \ensuremath{\frac{\omega}{\ensuremath{p}}} < 0.4, and is less than 0.01\% for frequencies up to 20\% of the natural frequency of the unit.

Many accelerometers, typically piezoelectric, have almost no damping so the usable frequency range is much smaller, up to about 10\% of the natural frequency for a 1\% error. Note however that these accelerometers tend to have quite large natural frequencies to begin with so the usable range is still quite appreciable.

Force Transmitted in Damped Base Excitation

During base excitation of a damped spring–mass system, the force transmitted between the support and the mass depends on the relative motion between the two and is transmitted through both the spring and the damper. Referring to Figure 5.11(b), the total force transmitted can be expressed as

(5.35)   \[F_T = k \bigl( x-y \bigr) + c \bigl( \dot{x}-\dot{y} \bigr) \\\]


or, in terms of the relative motion,

    \[F_T = k z + c \dot{z}\]

We could use either of these expressions since we have already found solutions for x(t) and z(t) previously for this situation. However, it is much easier to proceed by comparing equations (5.35) and (5.23) to note that

    \[F_T= -m \ddot{x}\]

We have already shown (equation (5.28)) that the response of the mass is given by

    \[x(t) = \mathbb{X} \sin (\omega t - \phi)\qquad\text{where}\qquad\mathbb{X} = \frac{a \, \sqrt{1 + \bigl(2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \bigr)^2}}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}.\]

so that the maximum acceleration is \mathbb{X} \omega^2. The maximum force transmitted is then

    \[\ensuremath{F_{\text{T}_\text{max}}} = m \Bigl[ \mathbb{X} \omega^2 \Bigr] = \left(\frac{k}{\ensuremath{p}^2}\right) \mathbb{X} \omega^2 =k \frac{\omega^2}{\ensuremath{p}^2} \frac{a \, \sqrt{1 + \bigl(2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \bigr)^2}}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}},\]


which can be rearranged as

(5.36)   \[\boxed{ \frac{\ensuremath{F_{\text{T}_\text{max}}}}{ka} = \frac{\ensuremath{\left(\dfrac{\omega}{\ensuremath{p}}}\right)^2 \sqrt{1 + \bigl(2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \bigr)^2}}{\ensuremath{\sqrt{\Bigl[1-\ensuremath{\bigl(\frac{\omega}{\ensuremath{p}}\bigr)}^2\Bigr]^2 + \Bigl[2 \zeta \ensuremath{\frac{\omega}{\ensuremath{p}}} \Bigr]^2}}}}\]

Equation (5.36) represents the transmissibility in the case of base excitation of a damped spring–mass system. As with the undamped situation discussed previously, the maximum disturbing force is again interpreted here to be \ensuremath{F_{\text{D}}}=ka. Figure 5.16 represents this relationship.

Figure 5.16: Transmissibility for base excitation of a damped system

Video Lecture: Forced Vibration of Damped SDOF Systems Section 5.2

Page Comments

  1. muhammad hasnain says:
    May 17, 2021 at 7:32 am

    why dont you consider the mass of the spring?
    i just need to know that, if i consider the mass of the ‘moving spring’ also then the results[ x(t) ] would be changed??

    Reply

Leave a Reply

Your email address will not be published.