Sound and Acoustics: Sound Power Level
Sound power level is a measure of the rate at which acoustic energy is radiated from a sound source. More loosely it is a measure of the ability of a device to produce sound. This is different from sound pressure level, which depends on additional factors, most importantly the distance from the sound source as we will see.
As with pressure magnitudes, there is a wide variety of sound powers associated with everyday acoustic phenomenon. To make these more manageable a decibel scale is once again used. The sound power level is defined as
(12.28) ![]()
where
![]()
The reference power level ![]() is the rate at which energy is transferred to the ear for a barely perceptible sound (the hearing threshold) at 2000 HZ. If this energy were converted to heat, it would take over 180 000 years to raise the temperature of 1 gram of water 1oC.
is the rate at which energy is transferred to the ear for a barely perceptible sound (the hearing threshold) at 2000 HZ. If this energy were converted to heat, it would take over 180 000 years to raise the temperature of 1 gram of water 1oC.
Note that the sound power level can also be expressed as
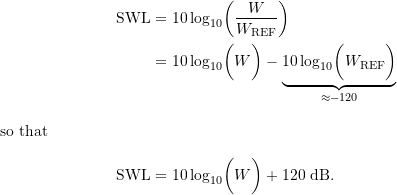
This can be inverted to find the power from the sound power level as
![]()
The table below illustrates sound power levels and powers associated with some common sounds.

Sound Intensity
Sound intensity measures the acoustic power passing through a unit area,
(12.29) ![]()
where
![]()
For a freely propagating plane wave, the average sound intensity is related to the sound pressure by
(12.30) ![]()
where
![Rendered by QuickLaTeX.com \begin{align*} I &= \text{Sound intensity } (\ensuremath{\text{W}}/m^2), \\[2mm] P &= \text{RMS pressure of sound wave } (\ensuremath{\text{Pa}}), \\[2mm] \rho &= \text{Density of medium } (\ensuremath{\text{kg}}/m^3), \\[2mm] \ensuremath{c} &= \text{Speed of sound in medium } (m / s). \end{align*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-89c2f0643045d83ed9a4574fff27db90_l3.png)
We can use these results to relate sound power levels and sound pressure levels.
Point Source
Consider a single sound source radiating sound uniformly in all directions (spherically) as illustrated in Figure 12.6. At a distance ![]() away from the source, all of the sound power from the source is passing through the area of a sphere of radius
away from the source, all of the sound power from the source is passing through the area of a sphere of radius ![]() . The sound intensity is then
. The sound intensity is then
![]()
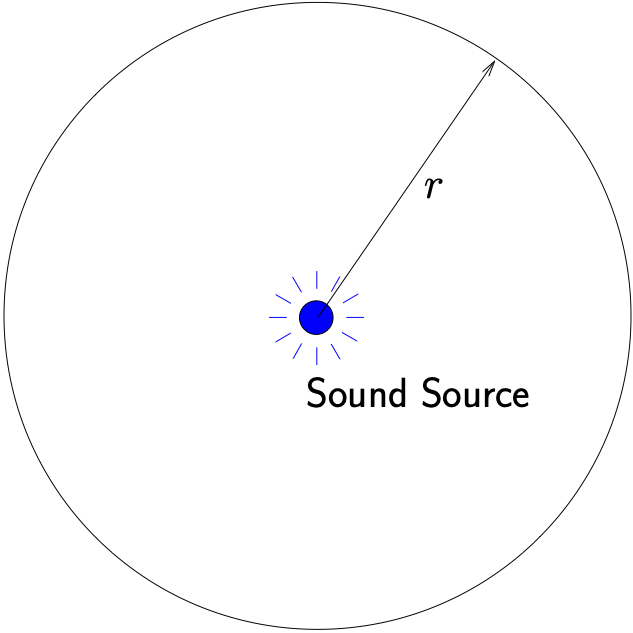
Figure 12.6: Sound propagating uniformly from a single point source
which can be seen to vary with distance from the source and follows an inverse square law. Using 12.30 we find that
![]()
so that
![]()
and dividing both sides by ![]() results in
results in
(12.31) ![]()
However, we note that
![]()
and that
![]()
so that
![]()
Substituting this into 12.31 we get
(12.32) ![]()
(12.33) ![]()
For air at 1 atmosphere and 15 °C,
![]()
so that ![]() . Therefore we find
. Therefore we find
![]()
so that 12.33 becomes
(12.34) ![]()
Taking the logarithm of both sides of 12.34 and multiplying by 10 results in
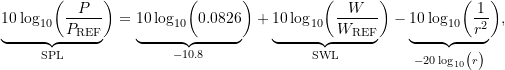
or
![]()
which is a relationship between sound power level, sound pressure level and distance from the source.
Alternatively, another useful relationship can be obtained by starting with 12.33 rewritten as
![]()
Taking the logarithm of both sides and multiplying by 10 results in
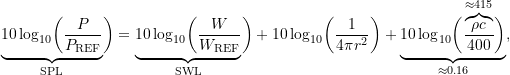
or
![]()
(12.35) ![]()
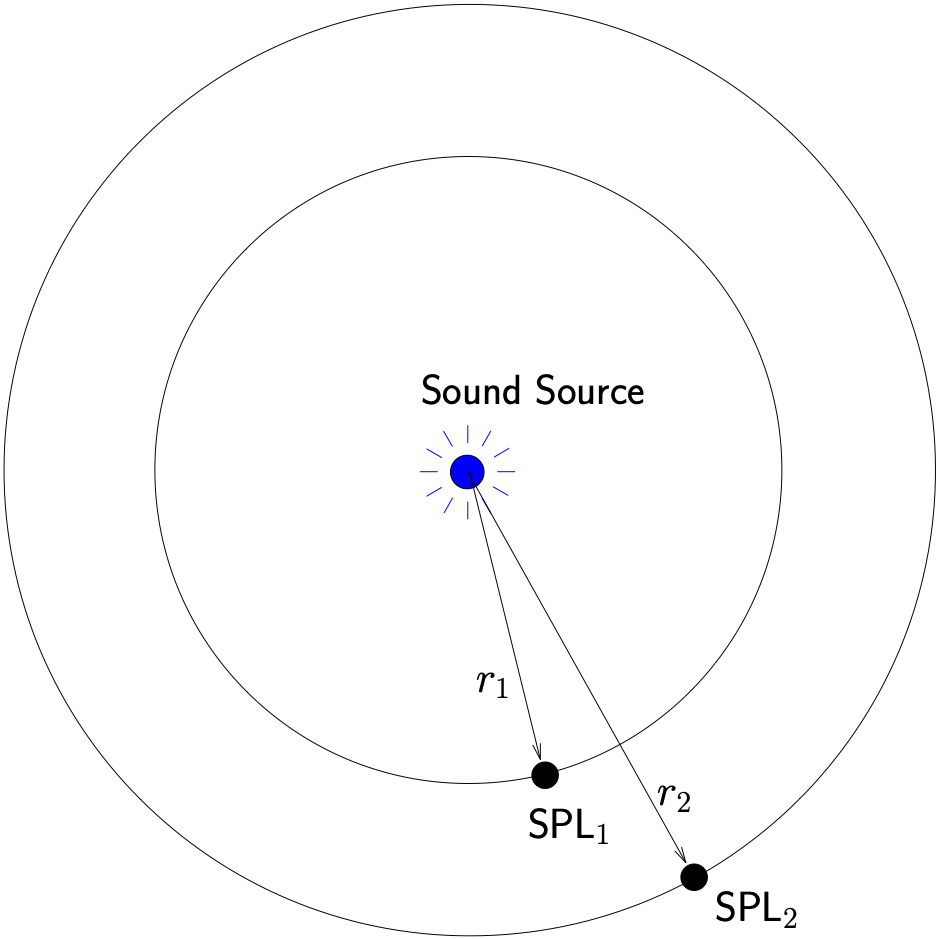
Figure 12.7: Variation of sound pressure level with distance from a point source.
We can used this result to determine how sound pressure level changes with distance from a sound source. Consider the situation shown in Figure 12.7 where the sound pressure level is known at one location and we would like to determine the sound pressure level at some other position. At at distance ![]() we know using 12.35 that
we know using 12.35 that
(12.36) 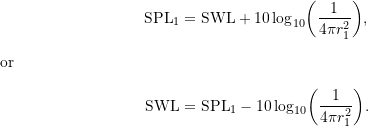
(12.37) ![]()
Combining these results shows that

(12.38) ![]()
Consider for example what happens if the distance from a point source is doubled (![]() ). In that case,
). In that case,

(12.39) ![]()
We see that the sound pressure level is reduced by 6 ![]() if the distance from a point source is doubled.
if the distance from a point source is doubled.
Reflecting Surfaces
In some situations the noise produced by a sound source does not travel uniformly in all directions. Often some of the acoustic waves reflect off of nearby surfaces. This sound energy then travels through other parts of the acoustic field which has the effect of increasing the sound pressure levels in these areas. This causes an increase in the apparent acoustic power of the sound source.
To account for the presence of nearby reflective surfaces, a directivity factor ![]() can be introduced. Using this directivity factor, the relationship between the sound pressure level and the sound power level of a point sound source shown in 12.35 can be rewritten more generally as
can be introduced. Using this directivity factor, the relationship between the sound pressure level and the sound power level of a point sound source shown in 12.35 can be rewritten more generally as
(1) ![]()

Figure 12.8: Directivity factor for some common situations
The directivity factor for some simple situations is shown in Figure 12.8.
Example
The tone from a tuning fork is at 440 Hz and has a measured sound pressure level of 54 dB at10 m.
- Determine the acoustic power of the tuning fork in this situation.
- Determine the sound pressure level at 20 m.
Assume that the sound waves are radiating uniformly in all directions (spherically) and that no reflecting surfaces are present.
Line Source
Another type of common noise source is a line source in which noise is generated (approximately) continuously along a straight line. Some typical examples include traffic noise on a busy highway or the noise from a long pipeline carrying high velocity steam.
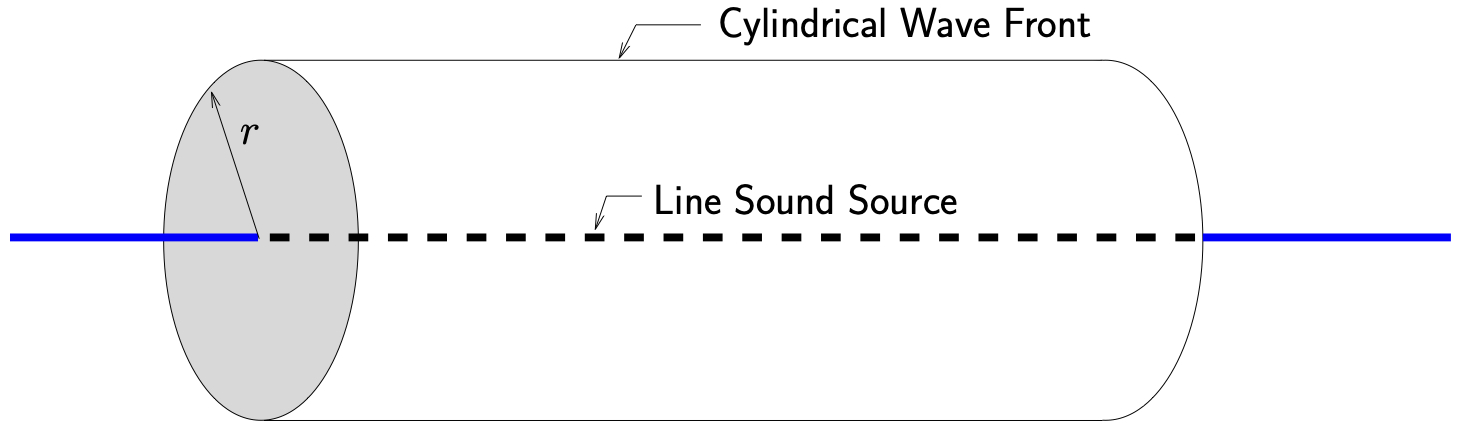
Figure 12.9: Schematic of sound propagation for a line sound source
To determine the propagation characteristics of sound in such a situation, we note that the sound waves will propagate away from the line source cylindrically (as opposed to spherically for a point source) as illustrated in Figure 12.9. As a result, considering the sound intensity at a distance ![]() from the line source we find that
from the line source we find that
![]()
where ![]() in this case is the power per unit length of the source times the distance
in this case is the power per unit length of the source times the distance ![]() under consideration. As can be seen, the intensity decreases linearly with
under consideration. As can be seen, the intensity decreases linearly with ![]() as opposed to the point source situation for which the intensity decrease with
as opposed to the point source situation for which the intensity decrease with ![]() .
.
As with the point source, we can determine a useful relationship between the sound pressure levels at different distances from the sound source. Following a development similar to that for a point source we can show that
(12.41) ![]()
which illustrates how the sound pressure level changes with distance from the line source. Once again, the sound power level is not required to use this relationship.
As with the point source, consider what happens if the distance from a line source is doubled. With ![]() , we can use 12.41 to show that
, we can use 12.41 to show that
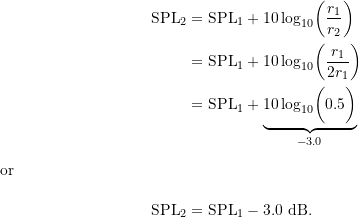
Doubling the distance from a line source reduces the sound pressure level by 3 ![]() (compared to 6
(compared to 6 ![]() for a point source) .
for a point source) .
Sound Intensity Level
Sound intensities vary over a wide range encompassing several orders of magnitude. As with sound pressure and sound power, a logarithmic scale is typically used when dealing with sound intensities. The sound intensity level is defined as
(12.42) ![]()
where
![Rendered by QuickLaTeX.com \begin{align*} I &= \text{Sound intensity}\ \Bigl(\frac{\ensuremath{\text{W}}}{m^2}\Bigr), \\[2mm] \ensuremath{I_{\text{REF}}} &= \text{Reference sound intensity}\ \Bigl(\ensuremath{I_{\text{REF}}} = 10^{-12}\ \frac{\ensuremath{\text{W}}}{m^2}\Bigr). \end{align*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4a32ccde44f42874d53cdbb9456e05cf_l3.png)

Thank you for the very clear breakdown of the topic – SOUND AND ACOUSTICS: SOUND POWER LEVEL.
Is it possible that there is a typo in the steps before the equation 12.35?
I am referring in particular to the “S”” in the equation for SPL.
Thank you once again