Open Educational Resources

Approximate Methods for Multiple Degree of Freedom Systems: Rayleigh’s Quotient

For a conservative MDOF system, the total mechanical energy E is a constant so that

    \begin{equation*}T + U = E\end{equation*}

or using the representations in (9.1) and (9.2)

(9.3)   \begin{equation*} \frac{1}{2} \bigl\{\!\dot{q}\!\bigr\}^{T} \!\!\bigl[m\bigr]\! \bigl\{\!\dot{q}\!\bigr\} +\frac{1}{2} \bigl\{\!q\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[k\bigr]\! \bigl\{\!q\!\bigr\} = E\end{equation*}

Now consider the system vibrating in one of its normal modes at a natural frequency \ensuremath{p}. The amplitudes of the coordinates are given by

    \begin{equation*}\bigl\{\!q\!\bigr\}= A \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{5pt}{0pt} \sin\left(p t + \phi\right)\end{equation*}

where \bigl\{\!\Phi\!\bigr\}\!\!\rule[3mm]{0pt}{0pt} is the corresponding mode shape and A is a constant. The derivatives of the coordinates will therefore be

    \begin{equation*}\bigl\{\!\dot{q}\!\bigr\} = A \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{3pt}{0pt} \ensuremath{p} \cos\left(p t + \phi\right)\end{equation*}

The coordinates will have maximum values given by

(9.4)   \begin{equation*} \bigl\{\!q\!\bigr\}_{\text{MAX}} = A \bigl\{\!\Phi\!\bigr\}{}\end{equation*}

which all occur simultaneously (when \sin\left(p t + \phi\right)=1). At the same instant, \cos\left(p t + \phi\right)=0 so the derivatives of the coordinates will all be zero (\bigl\{\!\dot{q}\!\bigr\}=0).

Similarly the coordinate derivatives will have maximum values given by

(9.5)   \begin{equation*} \bigl\{\!\dot{q}\!\bigr\}_{\text{MAX}} = A p \bigl\{\!\Phi\!\bigr\}{}\end{equation*}

when \cos\left(p t + \phi\right)=1. At this instant, \sin\left(p t + \phi\right)=0 so the coordinates themselves are all zero (i.e. the system is passing through its equilibrium configuration).

In summary

    \begin{align*}\sin\left(p t + \phi\right)&=1: \qquad & \bigl\{q\bigr\}_{\text{MAX}} &= A \bigl\{\Phi\bigr\} \qquad & \bigl\{\dot{q}\bigr\} &= 0 \\\cos\left(p t + \phi\right)&=1: \qquad & \bigl\{ q\bigr\}&= {0} \qquad & \bigl\{\dot{q} \bigr\}_{\text{MAX}} &= A \ensuremath{p} \bigl\{\Phi\bigr\}\end{align*}

Now, consider equation (9.3) at the instant when \sin\left(p t + \phi\right)=1. We see that

    \begin{align*}\frac{1}{2} \bigl\{\!\dot{q}\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[m\bigr] \! \bigl\{\!\dot{q}\!\bigr\} +\frac{1}{2} \bigl\{\!q\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!_{\text{MAX}}\!\bigl[k\bigr] \! \bigl\{\!q\!\bigr\}_{\text{MAX}} &= E \nonumber \\\frac{1}{2} \Bigl(A \!\bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\Bigr) \!\!\bigl[k\bigr] \! \Bigl(\! A \bigl\{\!\Phi\!\bigr\} \!\Bigr) &= E\end{align*}

or

(9.6)   \begin{equation*} \frac{1}{2} A^2 \bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[k\bigr] \! \bigl\{\!\Phi\!\bigr\} &= E.\end{equation*}

Similarly, when \cos\left(p t + \phi\right)=1 we find

    \begin{align*}\frac{1}{2} \bigl\{\!\dot{q}\!\bigr\}_{\text{MAX}}\!\bigl[m\bigr]\! \bigl\{\!\dot{q}\!\bigr\}_{\text{MAX}} +\frac{1}{2} \bigl\{\!q\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[k\bigr] \! \bigl\{\!q\!\bigr\} &= E \\\frac{1}{2} \Bigl( \! A p \bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\Bigr) \!\!\bigl[m\bigr] \! \Bigl(\! A p \bigl\{\!\Phi\!\bigr\} \!\Bigr) &= E\end{align*}

or

(9.7)   \begin{equation*} \frac{1}{2} A^2 p^2 \bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[m\bigr] \! \bigl\{\!\Phi\!\bigr\} &= E\end{equation*}

Since the total energy E is a constant for this conservative system, comparing equations (9.6) and (9.7 ) leads to the conclusion that

    \[\cancel{\frac{1}{2}A^2}\{\Phi\}^T[k]\{\Phi\} = \cancel{\frac{1}{2}A^2}p^2\{\Phi\}^T[m]\{\Phi\}\]

or

(9.8)   \begin{equation*} \boxed{p^2 = \frac{\hspace{-1cm}\bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[k\bigr] \! \bigl\{\!\Phi\!\bigr\} \rule{-3mm}{0pt}}{\bigl\{\!\Phi\!\bigr\}\!\rule[4mm]{0pt}{0pt}^{T} \!\!\bigl[m\bigr] \! \bigl\{\!\Phi\!\bigr\} \rule{5mm}{0pt}}}\end{equation*}

Equation (9.8) is known as Rayleigh’s Quotient. This result tells us that if a mode shape corresponding to a particular natural frequency is used in the ratio in (9.8), then the result will be the associated natural frequency squared.

By itself this is not a particularly useful result since typically, knowing \bigl[k\bigr] and \bigl[m\bigr] for a particular system, we must find \ensuremath{p} as part of the process of determining the mode shapes in the first place. However, equation (9.8) can be useful for obtaining approximate natural frequencies for MDOF systems. In essence, what we do is estimate a mode shape \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{0pt}{0pt} for the system and Rayleigh’s Quotient returns an associated estimate of the natural frequency. Obviously, the choice of \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{0pt}{0pt}{1} will influence the value of the returned natural frequency, however it can be shown that if \ensuremath{p}_1, \ensuremath{p}_2, \dots,\ensuremath{p}_N are the N natural frequencies on an N degree of freedom system, then for any assumed mode shape \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{0pt}{0pt} the frequency \ensuremath{p} returned by Rayleigh’s Quotient satisfies

    \begin{equation*}p \ge \ensuremath{p}_1 \qquad\text{and}\qquad p \le \ensuremath{p}_N\end{equation*}

i.e. the frequency returned by Rayleigh’s Quotient will always be higher than the lowest natural frequency and lower than the highest natural frequency in the system. Typically we are more concerned with the lowest (fundamental) frequency in a system, for which Rayleigh’s Quotient establishes an upper bound. (This frequency also provides a lower bound on the highest natural frequency of a system but this is usually of less interest.)

Remarkably good estimates of the fundamental natural frequency can be obtained even if the assumed mode shape \bigl\{\!\Phi\!\bigr\}\!\!\rule[5mm]{0pt}{0pt} (also called a trial vector) is not equal to the actual first mode shape.

EXAMPLE

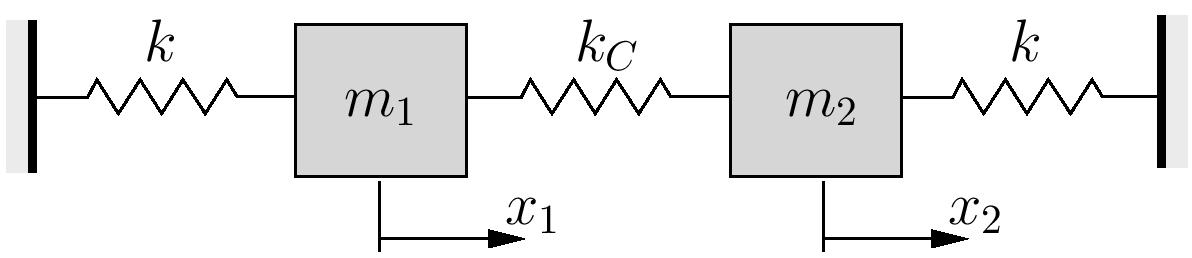
This image has an empty alt attribute; its file name is TDOF_Systems_Approx_Ex_002_Fig_a-eps-converted-to-page-001.jpg

(a) For the system shown above, estimate the fundamental natural frequency using Rayleigh’s Quotient. Assume m_1 = m_2 = m and use trial vectors of

    \begin{equation*}\bigl\{\!\Phi\!\bigr\} =\biggl\{\!\begin{array}{r}1 \\ 1 \\\end{array}\!\biggr\}, \qquad\bigl\{\!\Phi\!\bigr\} =\biggl\{\!\begin{array}{r}1 \\ -1 \\\end{array}\!\biggr\}, \qquad\bigl\{\!\Phi\!\bigr\} =\biggl\{\!\begin{array}{r}1 \\ 2 \\\end{array}\!\biggr\}, \qquad\bigl\{\!\Phi\!\bigr\} =\biggl\{\!\begin{array}{r}1 \\ -2 \\\end{array}\!\biggr\}\end{equation*}

and comment on the results. It was previously determined that

    \[\bigl[ k \bigr] =\biggl[\! \begin{array}{cc}k+k_C & -k_C \\-k_C & k+k_C \\\end{array} \!\biggr] , \qquad\bigl[ m \bigr] =\begin{bmatrix}m & 0 \\0 & m \\\end{bmatrix}\]

    \[p_1^2 = \frac{k}{m}, \qquad\bigl\{\!\Phi\!\bigr\}^{(1)} =\biggl\{\!\begin{array}{r}1 \\ 1 \\\end{array}\!\biggr\}, \qquad p_2^2 = \frac{k+2k_C}{m}, \qquad\bigl\{\!\Phi\!\bigr\}^{(2)} =\biggl\{\!\begin{array}{r}1 \\ -1 \\\end{array}\!\biggr\}\]

(b) Repeat the calculations in part (a) assuming m_1 = 2m, m_2=m, and k_C = 3k.

This image has an empty alt attribute; its file name is TDOF_Systems_Approx_Ex_002_Fig_b-eps-converted-to-page-001.jpg

Note that the exact solution in this case is

    \[p_1 \approx 0.809 \sqrt{\frac{k}{m}}, \qquad\bigl\{\Phi\bigr\}^{\textcircled{{\footnotesize{1}}}} \approx\biggl\{ \!\begin{array}{c}1.115 \\ 1 \\\end{array}\!\biggr\} \qquad \\\]

    \[p_2 \approx 2.312 \sqrt{\frac{k}{m}}, \qquad\bigl\{\!\Phi\!\bigr\}^{\textcircled{{\footnotesize{2}}}} \approx\biggl\{\!\begin{array}{c}-0.448 \\ 1 \\\end{array}\!\biggr\}\]

EXAMPLE

Use Rayleigh’s method to estimate the fundamental natural frequency for a light simply supported beam supporting three equally spaced identical masses.

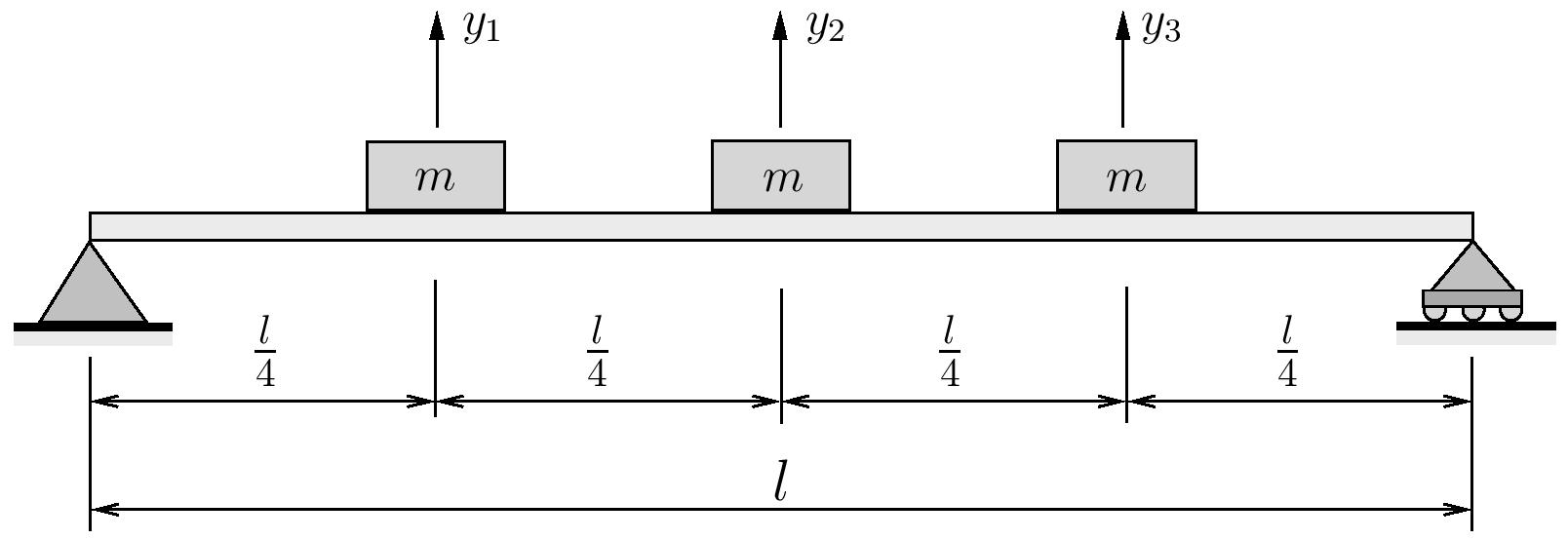
This image has an empty alt attribute; its file name is TDOF_Systems_Approx_Ex_004_Fig-eps-converted-to-page-001.jpg

Assume trial vectors of

    \begin{equation*}\bigl\{\!\Phi\!\bigr\} =\Biggl\{\!\begin{array}{r}1 \\ 1 \\ 1 \\\end{array}\!\Biggr\}, \qquad\bigl\{\!\Phi\!\bigr\} =\Biggl\{\!\begin{array}{r}1 \\ 2 \\ 1 \\\end{array}\!\Biggr\}, \qquad\bigl\{\!\Phi\!\bigr\} =\Biggl\{\!\begin{array}{r}1 \\ 1.5 \\ 1 \\\end{array}\!\Biggr\}\end{equation*}

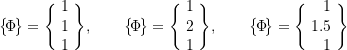
Note that for this problem

    \begin{align*}\bigl[ k \bigr] &=\frac{192 EI}{7 l^3}\Biggl[\begin{array}{rrr}23 & -22 & 9\\-22 & 32 & -22\\9 & -22 & 23\\\end{array}\vspace{4mm}\Biggr] \\\bigl[ m \bigr] &=m\Biggl[\begin{array}{ccc}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\\\end{array}\Biggr] \\\end{align*}

Page Comments

  1. David Stanion says:
    June 24, 2025 at 10:36 am

    Thank you. I am 82. At seven years of age I was labeled a total retard, unteachable and unlearnable by the Catholic Church. A nun, Sister Angela Cool did an experiment and I was allowed into regular class. Throughout life I have been denounced as an idiot savant. So what? We learn differently; with the main obstacle being being libeled as above; then removed from any and all stimuli including social interaction. Leave us alone. Let us learn. And we can really contribute to society and government in our own ways. That includes keeping the self-righteous, self-promoting, shady law enforcement and other such secretive organizations off our backs. My life was destroyed by two such FBI creatures, snake-headed skunks, that claimed I did not have the imagination to develop weapons and other things for the Navy. They robbed me of credit, merit, monetary awards, and my life to make themselves safe careers. Please see that it does not happen to other people like me. So I have a hobby of learniong through self research. And my country is robbed of the benefits.

    Reply

Leave a Reply to David Stanion Cancel reply

Your email address will not be published.