Open Educational Resources

Multiple Degree of Freedom Systems: Eigenvalue Problem

The problem of finding the natural frequencies and mode shapes for a multiple degree of freedom system is essentially an eigenvalue problem, although we have so far not presented it as such. To see this recall that the equations of motion for an MDOF system can be written as

(8.26)   \[ \ensuremath{\bigl[m\bigr]}\!\!\ensuremath{\bigl\{\ddot{x}\bigr\}} + \ensuremath{\bigl[k\bigr]}\!\!\ensuremath{\bigl\{x\bigr\}} = \ensuremath{\bigl\{0\bigr\}} \]

where [m] and [k] are the mass and stiffness matrices respectively and {x} is a column vector containing the coordinates. We look for solutions in which all of the coordinates are undergoing simple simultaneous harmonic motion of the form

    \[ \ensuremath{\bigl\{x\bigr\}} = \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} \ensuremath{\sin\left(\ensuremath{p} t + \phi\right)}, \]

so that

    \[ \ensuremath{\bigl\{\ddot{x}\bigr\}} = - \ensuremath{p}^2 \bigl\{\ensuremath{\mathbb{A}}\bigr\} \ensuremath{\sin\left(\ensuremath{p} t + \phi\right)}. \]

Substitution these results into the equations of motion gives

    \begin{gather*} - \ensuremath{p}^2 \ensuremath{\bigl[m\bigr]}\!\! \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} \ensuremath{\sin\left(\ensuremath{p} t + \phi\right)} + \ensuremath{\bigl[k\bigr]}\!\!\ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} \ensuremath{\sin\left(\ensuremath{p} t + \phi\right)} = \ensuremath{\bigl\{0\bigr\}}, \\ - \ensuremath{p}^2 \ensuremath{\bigl[m\bigr]}\!\! \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} + \ensuremath{\bigl[k\bigr]}\!\! \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \ensuremath{\bigl\{0\bigr\}}, \end{gather*}

or

(8.27)   \[ \ensuremath{\bigl[k\bigr]}\!\!\ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \ensuremath{p}^2 \ensuremath{\bigl[m\bigr]}\!\!\ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}}. \]

Pre-multiplying both sides of (8.27) by the inverse of the mass matrix gives

    \[ \underbrace{\ensuremath{\bigl[m\bigr]\!\!\rule[5mm]{0pt}{0pt}^{-1}}\!\!\!\ensuremath{\bigl[k\bigr]}}_{\ensuremath{\bigl[D\bigr]}} \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \ensuremath{p}^2 \underbrace{\ensuremath{\bigl[m\bigr]\!\!\rule[5mm]{0pt}{0pt}^{-1}}\!\!\ensuremath{\bigl[m\bigr]}}_{\ensuremath{\bigl[1\bigr]}} \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} \]

or

(8.28)   \[ \boxed{ \ensuremath{\bigl[D\bigr]}\!\!\ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \ensuremath{p}^2 \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} } \]

which is a standard eigenvalue problem

  • [D]=[m]^{-1}[k] is known as the dynamic matrix
  • the natural frequencies (squared) 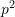p^2 are the eigenvalues of [D]
  • the mode shapes 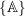{\mathbb{A}} are the associated eigenvectors of [D]

The dynamic matrix [D] can be used with standard software packages such as Matlab or Octave.
Alternatively, starting with equation (8.27) and premultiplying both side by [k]^{-1} gives

    \[ \underbrace{\ensuremath{\bigl[k\bigr]}i\!\!\ensuremath{\bigl[k\bigr]}}_{\ensuremath{\bigl[1\bigr]}} \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \ensuremath{p}^2 \underbrace{\ensuremath{\bigl[k\bigr]}i\!\!\ensuremath{\bigl[m\bigr]}}_{\large [D^*]} \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}}, \]

or

    \[ \boxed{ [D^*]\ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} = \frac{1}{\ensuremath{p}^2} \ensuremath{\bigl\{\!\ensuremath{\mathbb{A}}\!\bigr\}} } \]

which is another formulation of the standard eigenvalue problem.

Leave a Reply

Your email address will not be published. Required fields are marked *