Sound and Acoustics: Sound Pressure Level
The range of frequencies that human beings can hear varys from about 20 Hz to 20 000 Hz. The frequency of the sound affects the perceived pitch. The volume or loudness of the sound is related to the pressure level (the acoustic overpressure) of the sound
![]()
There is a wide range of pressure levels that can be experienced as “hearing”. The nominal threshold for human hearing is about ![]()
![]()
![]() at a frequency of 1000 Hz. This is about 0.00000002%
at a frequency of 1000 Hz. This is about 0.00000002% ![]() . At this pressure level, the resulting vibrations of the human eardrum are on the order of
. At this pressure level, the resulting vibrations of the human eardrum are on the order of ![]() cm or
cm or ![]() , which is about
, which is about ![]() the diameter of a hydrogen atom. At the other extreme, a loud jet engine has associated pressure levels of around 2000
the diameter of a hydrogen atom. At the other extreme, a loud jet engine has associated pressure levels of around 2000 ![]() (2%
(2% ![]() ) or even higher. There is a danger of rupture of the eardrum at these pressure levels.
) or even higher. There is a danger of rupture of the eardrum at these pressure levels.
The pressure range we deal with therefore covers about 8 orders of magnitude. To make it easier to deal with this wide range of values, a decibel scale (dB) is used. The sound pressure level(SPL) is defined as
(12.22) ![]()
where
![]()
Note that this can also be written as
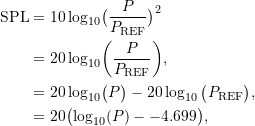
or
![]()
If required, the (RMS) pressure amplitude can be determined from the sound pressure level by
(12.23) ![]()
Note that most sound instrumentation is calibrated to work in decibels directly. In most cases the actual pressure amplitudes are not required and are not used (OHSA guidelines for example use decibels and not actual pressures).
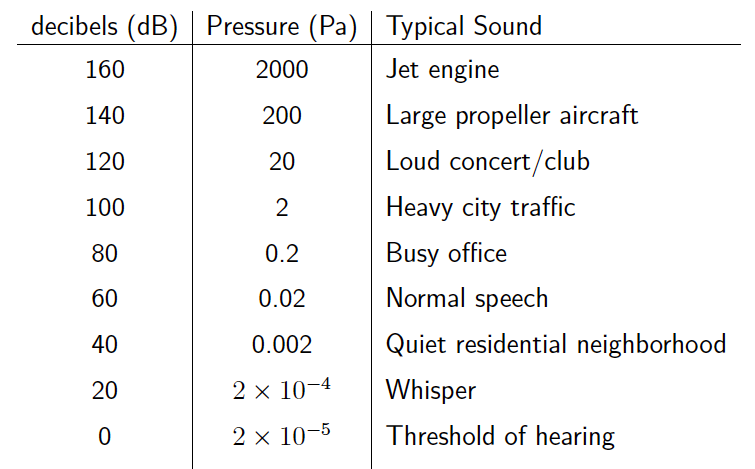
Table 12.2: Sound pressure levels and pressures for common sounds
Table 12.2 illustrates the sound pressure levels and pressures associated with sound common sounds.
Multiple Sources
If we have multiple uncorrelated sources of sound added together it can be shown that the resulting sound pressure level is
(12.24) ![]()
where
![]()
Consider two identical sources with pressure level ![]() . The sound pressure level for a single source is
. The sound pressure level for a single source is
![]()
When both sources are present, using 12.24 the sound pressure level becomes
![Rendered by QuickLaTeX.com \begin{align*} \ensuremath{\text{SPL}}_2 &= \ensuremath{10\log_{10}}\biggl ({\frac{P^2 + P^2}{\ensuremath{P_{\text{REF}}}^2}}\biggr ), \\[1mm] &= \ensuremath{10\log_{10}}\biggl ({\frac{2 P^2}{\ensuremath{P_{\text{REF}}}^2}}\biggr ), \\[1mm] &= \ensuremath{10\log_{10}}\biggl ({\frac{P^2}{\ensuremath{P_{\text{REF}}}^2}}\biggr ) + \underbrace{{\ensuremath{10\log_{10}}{2}}}_{=3.0} \end{align*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-42648e9b9f6671517860cf9034eb293d_l3.png)
(12.25) ![]()
This indicates that the sound pressure level increases by 3 dB when a second identical source is added as illustrated in Figure 12.5.
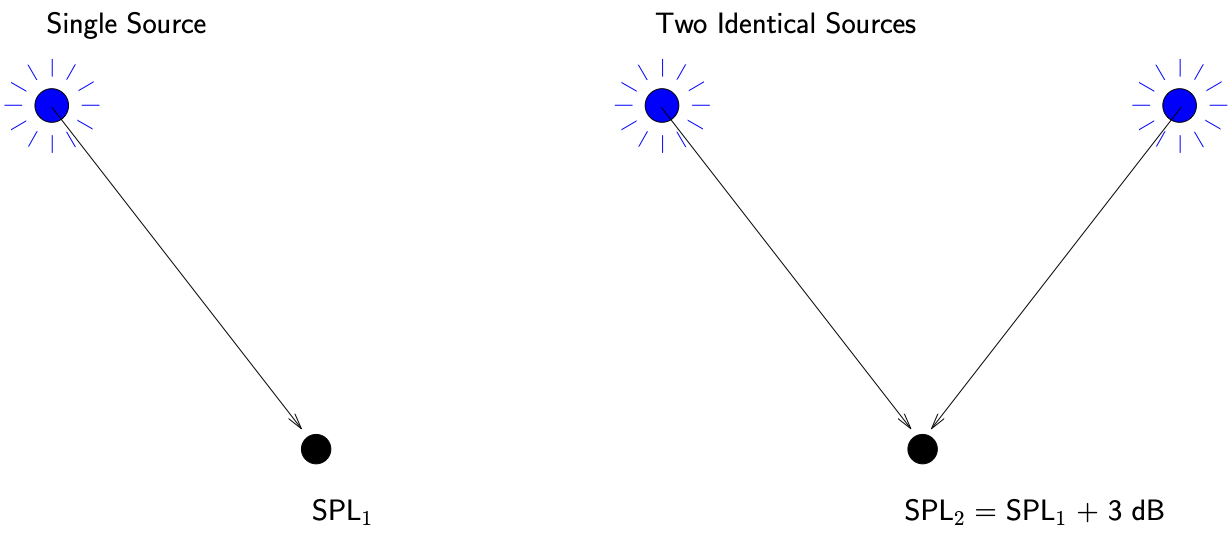
Figure 12.5: Sound pressure level from two identical sources
Now consider what happens when two sound sources are added together which are not identical. Assume that one sound source has an associated sound pressure level 10 dB higher than the other so that, for example,
![]()
This means that
![]()
or
![]()
where ![]() and
and ![]() are the (RMS) pressures associated with each sound source. When these sources are combined, the total pressure is then
are the (RMS) pressures associated with each sound source. When these sources are combined, the total pressure is then
![]()
so the total sound pressure level is
![]()
or
![]()
This is close to the sound pressure level of the loudest source in isolation. If the difference between the two sources was initially 20 dB, then the sound pressure level of the two sources added together would be the same (to one decimal place) as the loudest source in isolation.
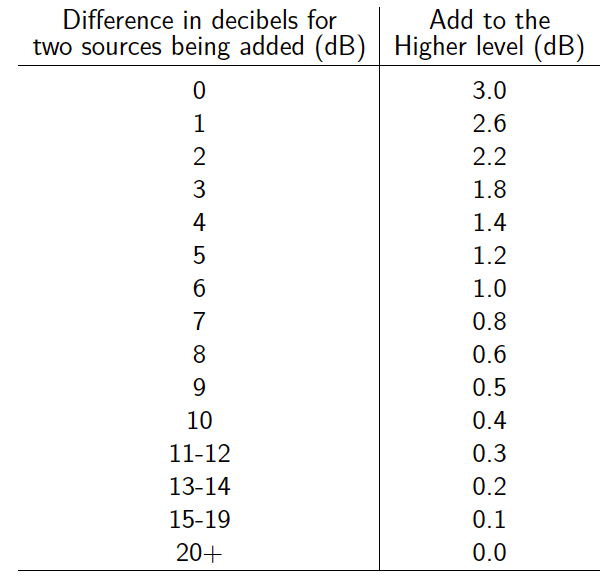
Table 12.3: Combining sound pressure levels
Table 12.3 shows the approximations that can be used for adding two sound sources together. To use this table, first find the difference in sound pressure level between the two sources to be added. Then the corresponding value from this table is added to the larger of two original sound pressure levels. These values have been rounded to the nearest 0.1 ![]() . For more accurate values, one would use the general result
. For more accurate values, one would use the general result
(12.26) ![]()
(12.27) ![]()
if more than two sources are present.
