Centres of Bodies: Center of gravity
Center of gravity, center of mass, and centroid are three similar concepts, which can be closely related under certain circumstances. This chapter will start with discussing the center of gravity, which is affected by the distribution of weight (or gravitational forces). Gravitational acceleration can be considered constant at any part of a body within the scope of this textbook. In this case, the center of mass coincides with the center of gravity of the same body. In some engineering analysis, we only need to consider the mass distribution of a body, not the weight. The center of mass will be discussed in the second section. Further with constant density all over a body, the center of gravity and the center of mass coincide with the centroid. In the last section, we introduce the centroid and prove that all the three concepts become equivalent under some conditions.
In many problems involving force analysis, the weight distribution or the total weight (resultant force) of a body may not be ignored and therefore should be involved in calculations . In those problems, the total weight and its location should be determined.
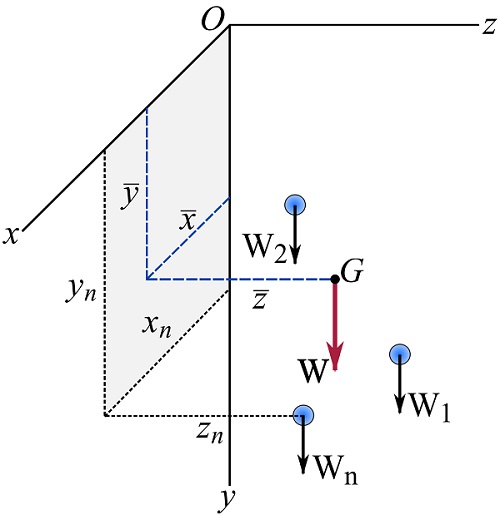
Assume a discrete system consisting of n particles that each has a mass of ![]() (Fig. 9.1a). Located in the Earth’s gravitational field, the weight of each particle is a force with a magnitude of
(Fig. 9.1a). Located in the Earth’s gravitational field, the weight of each particle is a force with a magnitude of ![]() (where
(where ![]() ) and a direction toward the Earth. The weights of all particles form a system of parallel forces as shown in Fig. 9.1a. The weights can be represented by an equivalent total (resultant) weight,
) and a direction toward the Earth. The weights of all particles form a system of parallel forces as shown in Fig. 9.1a. The weights can be represented by an equivalent total (resultant) weight,
(9.1a) ![]()
or in a scalar form,
(9.1b) ![]()
which acts at a point called the center of gravity of the system and denoted by ![]() .
.

The location of ![]() , of a system is determined by the requirement that the moment of the original force system about any point must equal the moment caused by the single resultant force about the same point (see Section 3.4). A Cartesian coordinate system at some point
, of a system is determined by the requirement that the moment of the original force system about any point must equal the moment caused by the single resultant force about the same point (see Section 3.4). A Cartesian coordinate system at some point ![]() in the space, as shown in Fig. 9.1b, can be set up to find the coordinates
in the space, as shown in Fig. 9.1b, can be set up to find the coordinates ![]() of
of ![]() . The coordinates of the particles and the
. The coordinates of the particles and the ![]() of a system can inform us about the location of
of a system can inform us about the location of ![]() relative to the particles. The moment of
relative to the particles. The moment of ![]() about each Cartesian axis should equal to the sum of the moments of
about each Cartesian axis should equal to the sum of the moments of ![]() about the same axis.
about the same axis.
As indicated by Fig. 9.1b, ![]() and
and ![]() are parallel to the z axis and therefore they produce moments only about the x and y axes. Equating the moments of the individual
are parallel to the z axis and therefore they produce moments only about the x and y axes. Equating the moments of the individual ![]() and
and ![]() about each of the x and y axes in scalar formulation,
about each of the x and y axes in scalar formulation,
About the x axis: ![]()
About the y axis: ![]()
leads to (the limits of the sum are not shown for the sake of conciseness),
(9.2) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\sum x_iW_i}{W}\\\bar y&=\frac{\sum y_iW_i}{W}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e4f7308c20c38b7aa31c1438f86adea6_l3.png)
where ![]() and
and ![]() are the magnitudes of the weights, and the coordinates
are the magnitudes of the weights, and the coordinates ![]() and
and ![]() are signed distances from the origin. The sign of a coordinate determines the sign of the moment.
are signed distances from the origin. The sign of a coordinate determines the sign of the moment.
Equations 9.2 sufficiently determine the points through which the lines of action of ![]() passes. These points have the common x and y coordinates of
passes. These points have the common x and y coordinates of ![]() and an arbitrary z coordinate (Fig. 9.1b). To determine the z coordinate (
and an arbitrary z coordinate (Fig. 9.1b). To determine the z coordinate (![]() ) of
) of ![]() , the body and the coordinate system are rotated about the x axis while preserving the location of the origin as demonstrated in Fig. 9.2 (the body and the coordinate system can be rotated arbitrarily). The weights are now parallel to the y axis. Equating the components of the moments of the two systems about the x axis indicates that,
, the body and the coordinate system are rotated about the x axis while preserving the location of the origin as demonstrated in Fig. 9.2 (the body and the coordinate system can be rotated arbitrarily). The weights are now parallel to the y axis. Equating the components of the moments of the two systems about the x axis indicates that,
(9.3) ![]()
Equations 9.2 and 9.3 imply that the coordinates of ![]() are unique and determined using,
are unique and determined using,
(9.4) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\sum x_iW_i}{W}\\\bar y&=\frac{\sum y_iW_i}{W}\\\bar z&=\frac{\sum z_iW_i}{W}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6dcb7ef9ccf67a31f9457b7aeac24bef_l3.png)
Remark: the location of the center of gravity does not depend on a coordinate system chosen for the calculations; it has an absolute location with respect to any point of the body.
Remark: center of gravity of a body is not necessarily a point of the body, but rather, it can be a point of the geometric space surrounding the body.
Example 9.1.1
Determine the center of gravity, ![]() , of the set of particles shown.
, of the set of particles shown.

SOLUTION
The total weight ![]() is
is ![]() . By Eq. 9.5, we can write,
. By Eq. 9.5, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\sum x_iW_i}{W}= \frac{(4)(15)+(-2)(20)+(0)(10)}{45}=0.44 \text{ m}\\\bar y&=\frac{\sum y_iW_i}{W}= \frac{(6)(15)+(1)(20)+(-3)(10)}{45}=1.78\text{ m}\\\bar z&=\frac{\sum z_iW_i}{W}= \frac{(-1)(15)+(3)(20)+(1)(10)}{45}=1.22\text{ m}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-555ea3474f3c75717da64a0bc6535b00_l3.png)
The following interactive example demonstrates the center of gravity of a set of particles. The particles are all located in a plane, say ![]() . Add particles (up to 10 particles) with different weights and arrange their locations by dragging them around to observe the variations in the location of the center of gravity.
. Add particles (up to 10 particles) with different weights and arrange their locations by dragging them around to observe the variations in the location of the center of gravity.
Equations 9.6 define the center of gravity for a discrete system which consists of a set of (a finite number of) particles or parts. A continuous physical body, however, consists of an infinite number of infinitely small particles. Determining the center of gravity of a continuous body is explained below.
Consider a continuous body in three dimensions (Fig. 9.3). The body can be divided into n small elements with size of ![]() , as shown in Fig 9.3. Each element can be regarded as a particle with weight of
, as shown in Fig 9.3. Each element can be regarded as a particle with weight of ![]() . If the coordinate of the center of gravity of an element is denoted as
. If the coordinate of the center of gravity of an element is denoted as ![]() , The coordinates of the center of gravity of the body can be approximately calculated as,
, The coordinates of the center of gravity of the body can be approximately calculated as,
(9.5) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\sum_i^n \tilde x_i\Delta W_i}{\sum_i^n\Delta W_i}\\\bar y&=\frac{\sum_i^n \tilde y_i\Delta W_i}{\sum_i^n\Delta W_i}\\\bar z&=\frac{\sum_i^n \tilde z_i\Delta W_i}{\sum_i^n\Delta W_i}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-15297bc2eb8e3e037ef052a21f2a34b5_l3.png)
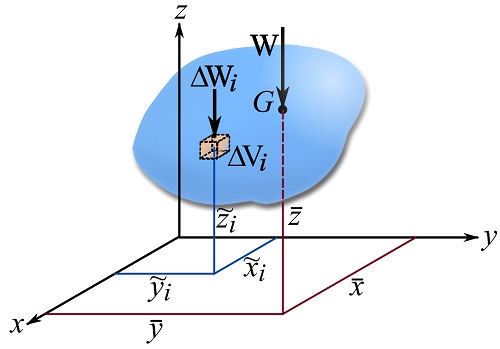
If the number of elements increases in the limit as ![]() (the sizes of the elements become infinitely small), then the above sums attain the following integral forms in the limit and uniquely determine the coordinates of the center of gravity of the body as,
(the sizes of the elements become infinitely small), then the above sums attain the following integral forms in the limit and uniquely determine the coordinates of the center of gravity of the body as,
(9.6) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V \tilde x dW}{\int_V dW}\\\bar y&=\frac{\int_V \tilde y dW}{\int_V dW}\\\bar z&=\frac{\int_V \tilde z dW}{\int_V dW}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-835efdd858d245ce5d7d392a6eee71d2_l3.png)
where ![]() denotes integration over the volume (
denotes integration over the volume (![]() ) of the body. The term
) of the body. The term ![]() equals
equals ![]() being the total weight of the body (Fig 9.3).
being the total weight of the body (Fig 9.3).
Since the integrals should be evaluated over all points of the the volume of the body, the concept of specific weight is used to write the integrals in the form of volume integrals. The Specific weight, ![]() of a material is defined as its weight per unit volume, i.e.
of a material is defined as its weight per unit volume, i.e. ![]() . Letting
. Letting ![]() the integrals in Eq. 9.6 can be written as,
the integrals in Eq. 9.6 can be written as,
(9.7) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V \tilde x \gamma dV}{\int_V \gamma dV}\\\bar y&=\frac{\int_V \tilde y \gamma dV}{\int_V \gamma dV}\\\bar z&=\frac{\int_V \tilde z \gamma dV}{\int_V \gamma dV}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b356ba56f56afea32b7390db182249ef_l3.png)
The specific weight ![]() can also be a function of location, i.e.
can also be a function of location, i.e. ![]() , meaning the specific weight of a body can be different at different places.
, meaning the specific weight of a body can be different at different places.
To implement the integrals in Eq. 9.7, we need to know the location of the centers of gravity of any differential element. If the elements are infinitely small (in all directions), we can assume the specific weight is constant for each element and the center of gravity can be considered at the geometric center (see Section 9.3) of the element. If the differential elements are cubes or in a cuboid shape, the size of each element can be written as ![]() , and since this element is infinitely small in all directions
, and since this element is infinitely small in all directions ![]() and
and ![]() . Thereby, Eqs. 9.7 become,
. Thereby, Eqs. 9.7 become,
(9.8a) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V x \gamma dV}{\int_V \gamma dV}\\\bar y&=\frac{\int_V y \gamma dV}{\int_V \gamma dV}\\\bar z&=\frac{\int_V z \gamma dV}{\int_V \gamma dV}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e2e9983a39ae0c07b5525444e471d6c5_l3.png)
and can take the form of triple integrals as,
(9.8b) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\iiint_V x \gamma dxdydz}{\iiint_V \gamma dxdydz}\\\bar y&=\frac{\iiint_V y \gamma dxdydz}{\iiint_V \gamma dxdydz}\\\bar z&=\frac{\iiint_V z \gamma dxdydz}{\iiint_V \gamma dxdydz}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fafcce47dfb2e0f34124344a8ba3320e_l3.png)
EXAMPLE 9.1.2
Find the total weight and the center of gravity of a right rectangular prism made of a material with a constant specific weight ![]() . The dimensions of the sides of the body are
. The dimensions of the sides of the body are ![]() ,
, ![]() , and
, and ![]() as shown.
as shown.
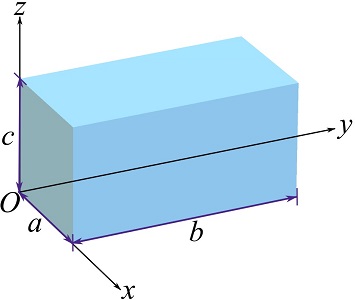
SOLUTION
Setting a Cartesian coordinate system as shown and using a cuboidal (cubic) differential element ![]() (see figure below), calculate the weight using the integral
(see figure below), calculate the weight using the integral ![]() . As
. As ![]() is constant, we can write,
is constant, we can write,
![]()
Note that the term ![]() equals the volume of the body which is, here, a rectangular cube with a volume of
equals the volume of the body which is, here, a rectangular cube with a volume of ![]() .
.
Considering a cuboidal differential element ![]() as shown, calculate the triple integrals in Eqs 9.8 for determining the center of gravity.
as shown, calculate the triple integrals in Eqs 9.8 for determining the center of gravity.

![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V x \gamma dV}{\int_V \gamma dV}=\frac{\int_V x dV}{\int_V dV}= \frac{1}{abc}\int_0^a\int_0^b\int_0^c x dxdydz\\&=\frac{1}{abc}\int_0^c\left(\int_0^b\left(\int_0^axdx\right)dy\right)dz=\frac{1}{abc}(bc\frac{a^2}{2})\\&=\frac{a}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-eb186f52b51466a9b3329290f9df98e8_l3.png)
Similarly,
![]()
briefly shown as,
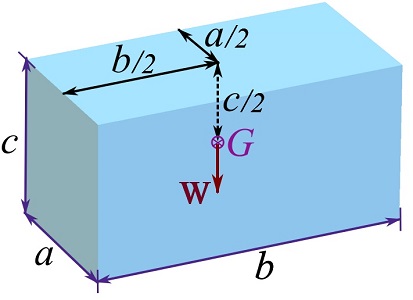
Using the volumetric differential element ![]() leads to triple integrals in a Cartesian frame. However, depending on the geometry of a body, it is possible to use other shapes for differential elements and write the integrals in Eqs. 9.7 as single-variable (one-dimensional) integrals. One approach is to choose prismatic elements with differential length along only one axis (as apposed to
leads to triple integrals in a Cartesian frame. However, depending on the geometry of a body, it is possible to use other shapes for differential elements and write the integrals in Eqs. 9.7 as single-variable (one-dimensional) integrals. One approach is to choose prismatic elements with differential length along only one axis (as apposed to ![]() being differential along three axes). To demonstrates this approach, we use differential elements having the shape of a right rectangular prism or a cuboid and solve the previous example again as follows.
being differential along three axes). To demonstrates this approach, we use differential elements having the shape of a right rectangular prism or a cuboid and solve the previous example again as follows.
EXAMPLE 9.1.3
Find the center of gravity and total weight of a right rectangular prism made of a material with a constant specific weight ![]() and dimensions as shown.
and dimensions as shown.

SOLUTION
Each equation in Eqs. 9.7 can be calculated independently, therefore, we can choose different volumetric elements for each equation.
To find ![]() , choose a differential element (with a volume of)
, choose a differential element (with a volume of) ![]() as shown in the following figure. The differential element is a right rectangular prism or a cuboid whose length in the x direction is
as shown in the following figure. The differential element is a right rectangular prism or a cuboid whose length in the x direction is ![]() . Because
. Because ![]() is small enough (approaching to zero), the center of gravity of the differential element,
is small enough (approaching to zero), the center of gravity of the differential element, ![]() , in the x direction is equal to x indicating the location of the differential element along the x axis.
, in the x direction is equal to x indicating the location of the differential element along the x axis.
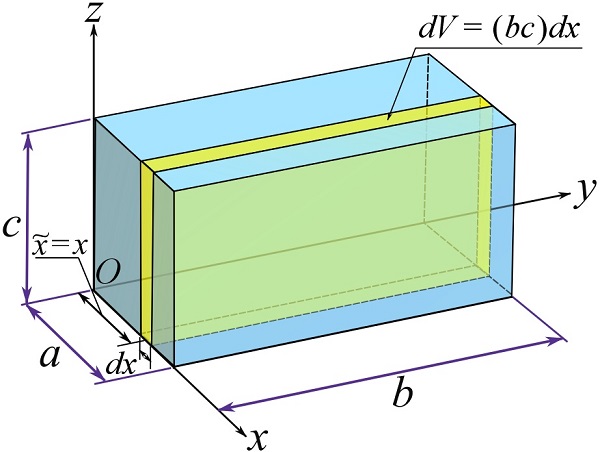
Consequently,
![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V \tilde x \gamma dV}{\int_V \gamma dV}=\frac{\int_V x \gamma (bc)dx}{\int_V \gamma (bc)dx}=\frac{\int_0^a x dx}{\int_0^a dx}= \frac{a^2}{2a}\\&=\frac{a}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-93a823f820d8b9cd1abdb69b6bee4243_l3.png)
To calculate ![]() , consider a volumetric differential element
, consider a volumetric differential element ![]() as shown in the figure. This is a prismatic element whose length
as shown in the figure. This is a prismatic element whose length ![]() in the y direction is infinitesimal; therefore,
in the y direction is infinitesimal; therefore, ![]() for the element.
for the element.
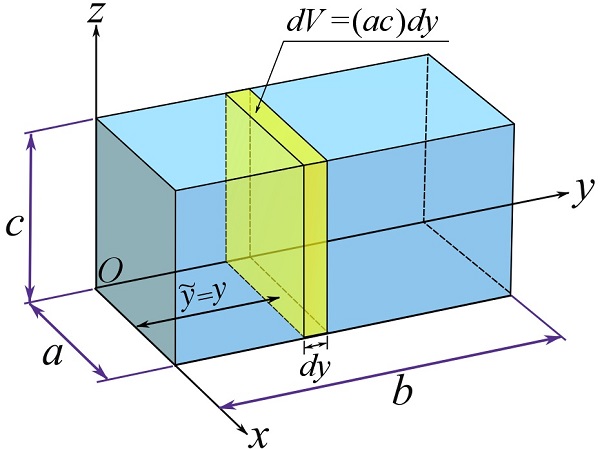
Similar to the previous calculations, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}\bar y&=\frac{\int_V \tilde y \gamma dV}{\int_V \gamma dV}=\frac{\int_V y \gamma (ac)dy}{\int_V \gamma (ac)dx}=\frac{\int_0^b y dy}{\int_0^b dx}= \frac{b^2}{2b}\\&=\frac{b}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-03db38e3b3b511b15c0ceb50c1979173_l3.png)
To calculate ![]() , consider a volumetric differential element
, consider a volumetric differential element ![]() shown in the figure. This implies that
shown in the figure. This implies that ![]() for the element.
for the element.
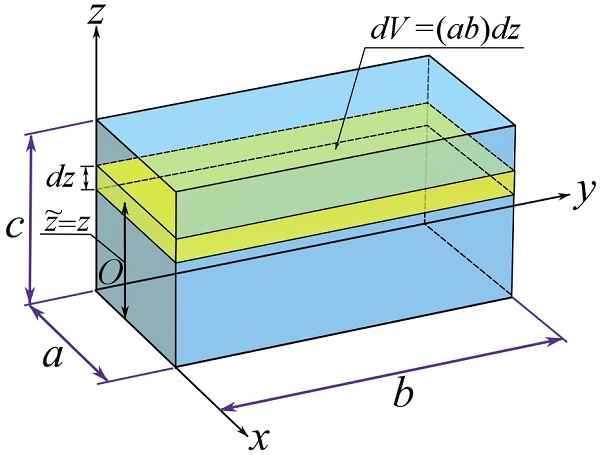
Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}\bar z&=\frac{\int_V \tilde z \gamma dV}{\int_V \gamma dV}=\frac{\int_V z \gamma (ab)dz}{\int_V \gamma (ab)dz}=\frac{\int_0^c z dz}{\int_0^c dz}= \frac{c^2}{2c}\\&=\frac{c}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-35854d15095f95c2551bf6d679140baf_l3.png)
As a result, the center of gravity of the rectangular prism is located at ![]() as also seen in Example 9.1.2.
as also seen in Example 9.1.2.
Calculate the weight using ![]() . As
. As ![]() is constant, any of the differential element can be used to write the integral as a single-variable integral.
is constant, any of the differential element can be used to write the integral as a single-variable integral.
![Rendered by QuickLaTeX.com \[\begin{split}W=&\int_V \gamma dV=\int_0^a \gamma (bc)dx =\int_0^b \gamma (ac)dy=\int_0^c \gamma (ab)dz\\=&\gamma (abc) = \gamma V\text{ N}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-24fb1c3a30fc8a3f1daa5129a60724bd_l3.png)
Remark: avoiding triple integrals by using prismatic elements makes the calculations easier in many cases.
In the previous example, the center of gravity of the rectangular prism was located at its geometric center ![]() naturally understood for the shape of a rectangular prism. The geometric center will be precisely defined in Section 9.3. Nevertheless, the center of gravity of a rectangular prism does not necessarily coincide with its geometric center if the body is made of a material with a varying specific weight. The following example clarifies this point.
naturally understood for the shape of a rectangular prism. The geometric center will be precisely defined in Section 9.3. Nevertheless, the center of gravity of a rectangular prism does not necessarily coincide with its geometric center if the body is made of a material with a varying specific weight. The following example clarifies this point.
EXAMPLE 9.1.4
The container shown in the figure contains a material (e.g fluid) with a specific weight linearly varying from the bottom to the top of the container, i.e. ![]() . Find the center of gravity of the fluid and its total weight.
. Find the center of gravity of the fluid and its total weight.
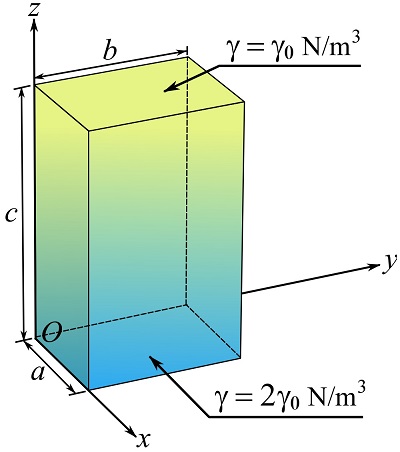
SOLUTION
Each equation in Eqs. 9.7 can be calculated independently, therefore, we can choose different volumetric elements for each equation.
To find ![]() , choose a differential element
, choose a differential element ![]() as shown in the following figure.
as shown in the following figure.
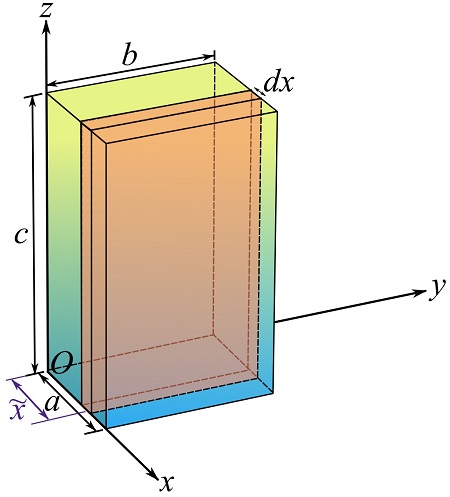
Consequently,
![Rendered by QuickLaTeX.com \[\begin{split}\bar x&=\frac{\int_V \tilde x \gamma (z) dV}{\int_V \gamma (z) dV}=\frac{\int_V x \gamma (z) (bc)dx}{\int_V \gamma (z) (bc)dx}=\frac{\int_0^a x \gamma (z) dx}{\int_0^a \gamma (z) dx}= \frac{\int_0^a x \gamma (z) dx}{\int_0^a \gamma (z) dx}=\frac{\int_0^a x dx}{\int_0^a dx}\\&=\frac{a}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-18272b4495d72b62b36c24643808f4db_l3.png)
Note that ![]() is a function of
is a function of ![]() and the integration is with respect to x.
and the integration is with respect to x.
To calculate ![]() , consider the volumetric differential element
, consider the volumetric differential element ![]() shown in the figure. This implies that
shown in the figure. This implies that ![]() for the element.
for the element.
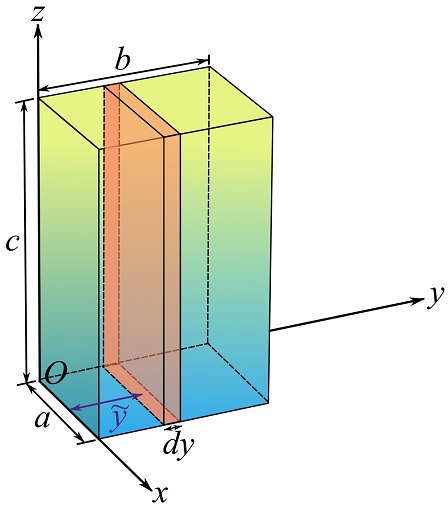
Similar to the previous calculations, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}\bar y&=\frac{\int_V \tilde y \gamma (z) dV}{\int_V \gamma (z) dV}=\frac{\int_V y \gamma (z) (ac)dy}{\int_V \gamma (z) (ac)dy}=\frac{\int_0^b y \gamma (z) dy}{\int_0^b \gamma (z) dy}= \frac{\int_0^b y \gamma (z) dy}{\int_0^b \gamma (z) dy}=\frac{\int_0^b y dy}{\int_0^b dy}\\&=\frac{b}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-72a5bae64632854bd5ccf5ea0a536f40_l3.png)
We can also obtain ![]() and
and ![]() by noticing that the weight of each element is constant, or the specific weight is uniform in the x and y directions.
by noticing that the weight of each element is constant, or the specific weight is uniform in the x and y directions.
To find ![]() , consider the following differential element and write the integration for the z direction. Note that
, consider the following differential element and write the integration for the z direction. Note that ![]() is a function of z and the integration is also with respect to z.
is a function of z and the integration is also with respect to z.

![Rendered by QuickLaTeX.com \[\begin{split}\bar z&=\frac{\int_V \tilde z \gamma (z) dV}{\int_V \gamma (z) dV}=\frac{\int_V z \gamma_0(\frac{-1}{c}z + 2) (ab)dz}{\int_V \gamma_0(\frac{-1}{c}z + 2) (ab)dz}=\frac{\int_0^c z (\frac{-1}{c}z + 2) dz}{\int_0^c (\frac{-1}{c}z + 2) dz}\\ &=\frac{4}{9}c\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d8f28ea8994e129f1312ae4ff890cbc8_l3.png)
Briefly, ![]()
Note that, in general, if ![]() is not constant in least one direction, the center of gravity does not locate at the (geometric) center for a rectangular prism.
is not constant in least one direction, the center of gravity does not locate at the (geometric) center for a rectangular prism.
To calculate the total weight, we should use a prismatic differential element (right rectangular prism) inside which ![]() is almost constant. Because
is almost constant. Because ![]() is a function of z, its value within the element
is a function of z, its value within the element ![]() is constant, or approaching a constant value, as
is constant, or approaching a constant value, as ![]() is small enough. Therefore,
is small enough. Therefore,
![]()
Composite bodies
A composite body is a (continuous) body that is composed of several sub-bodies possibly with different or same specific weights. To calculate the center of gravity of a composite body composed of several sub-bodies with volumes ![]() and specific weights
and specific weights ![]() , each integration in Eq. 9.7 (or Eqs. 9.6) becomes the sum of the integrations over all the composing bodies,
, each integration in Eq. 9.7 (or Eqs. 9.6) becomes the sum of the integrations over all the composing bodies,
![Rendered by QuickLaTeX.com \[\begin{split}\bar x&= \frac{\sum_{i=1}^n\int_{V_i} \tilde x \gamma_i dV}{\sum_1^n\int_{V_i} \gamma_i dV}\\\bar y&= \frac{\sum_{i=1}^n\int_{V_i} \tilde y \gamma_i dV}{\sum_1^n\int_{V_i} \gamma_i dV}\\\bar z&= \frac{\sum_{i=1}^n\int_{V_i} \tilde z \gamma_i dV}{\sum_1^n\int_{V_i} \gamma_i dV}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c2ac43aaa64f660e4efbd82b1441853a_l3.png)
With ![]() , the above equations can be written as,
, the above equations can be written as,
(9.9) ![Rendered by QuickLaTeX.com \[\begin{split}\bar x&= \frac{\sum \tilde x_i W_i}{\sum W_i}\\\bar y&= \frac{\sum \tilde y_i W_i}{\sum W_i}\\\bar z&= \frac{\sum \tilde z_i W_i}{\sum W_i}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-59e45e6163b239ea044fd4ac265b1ccc_l3.png)
where ![]() and
and ![]() denote the coordinates of the center of gravity of each sub- body. Equation 9.9 indicates that each composing body with weight
denote the coordinates of the center of gravity of each sub- body. Equation 9.9 indicates that each composing body with weight ![]() and its center of gravity located at
and its center of gravity located at ![]() is replaced by its own total weight
is replaced by its own total weight ![]() and located at
and located at ![]() , as what we have seen in Eqs. 9.4.
, as what we have seen in Eqs. 9.4.
EXAMPLE 9.1.5
Find the center of gravity of the composite body shown. Each body has a constant ![]() .
.

SOLUTION
To determine the center of gravity of the composite body, we need to determine the weight of each sub-body and express the centers of gravity with respect to the origin of one fixed coordinate system.
Since ![]() is constant for each body, determine its center of gravity according to the formulation derived in Example 9.1.2. The following figure shows the calculated center of gravity of each body. The locations of the centers of gravity are independently determined for each body.
is constant for each body, determine its center of gravity according to the formulation derived in Example 9.1.2. The following figure shows the calculated center of gravity of each body. The locations of the centers of gravity are independently determined for each body.
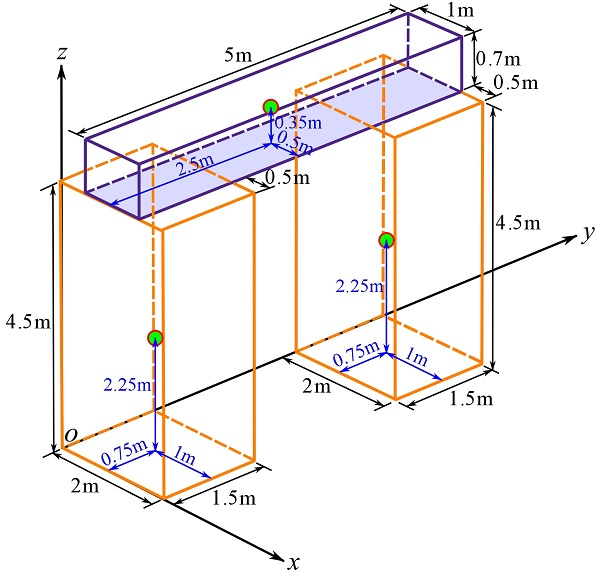
The weights of the bodies are ![]() . Therefore,
. Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}\bar x &= \frac{(0.5+0.5)(7)+(1)(10)+(1)(10)}{7+10+10}= 1\text{ m}\\\bar y &= \frac{(2.5)(7)+(0.75)(10)+(5-0.75)(10)}{7+10+10}=2.5\text{ m}\\\bar z &= \frac{(4.5+0.35)(7)+(2.25)(10)+(2.25)(10)}{7+10+10}=2.92\text{ m}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-86b5b469814e58ec95110d71254a16a4_l3.png)
Videos
Centre of Gravity (Composite Body):
Centre of Gravity (Continuous Body):
