Moments of Inertia of area: Composite areas
In the context of calculating the moment of inertia, a composite area is an area consisting of several non-overlapping (disjoint) sub-areas. The boundaries specifying the sub-areas can be explicitly declared by the geometry or arbitrarily chosen. Considering an area as a composite area is to simplify the calculation of the moment of inertia of the whole area. having simple shapes with already known or given formulations of moments of inertia
Consider an area ![]() consisting of (or partitioned into) n disjoint sub-areas denoted as
consisting of (or partitioned into) n disjoint sub-areas denoted as ![]() (Fig. 10.12).
(Fig. 10.12).

Then by the definition (Eq. 10.1), the moment of inertial of ![]() about an axis m can be written as,
about an axis m can be written as,
(10.10) ![Rendered by QuickLaTeX.com \[\begin{split}I_m&=\int_A D^2 dA=\sum_{i=1}^n \int_{A_i} D^2 dA\\&=\sum_{i=1}^n I_{im}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2999ac1999c6e1b29c285640d671c00a_l3.png)
where ![]() denotes the moment of inertia of the i-th area about the m axis. This results expresses that the moment of inertia of an area about an axis (m) is the sum of the moments of inertia of its (disjoint) sub-areas about the same common axis (m).
denotes the moment of inertia of the i-th area about the m axis. This results expresses that the moment of inertia of an area about an axis (m) is the sum of the moments of inertia of its (disjoint) sub-areas about the same common axis (m).
The same result also holds for the polar moments of inertia of an area and its sub-areas; meaning that,
(10.11) ![Rendered by QuickLaTeX.com \[\begin{split}J_O&=\int_A r^2 dA=\sum_{i=1}^n \int_{A_i} r^2 dA\\&=\sum_{i=1}^n J_{iO}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-927f59e54dee77937a0a755cc24515c2_l3.png)
where ![]() denotes the polar moment of inertia of the i-th area about the (common) point
denotes the polar moment of inertia of the i-th area about the (common) point ![]() .
.
Remark: When we sum the values of the moments of inertia (of sub-areas), the values have to be calculated about a common axis. A hint for problem solving is to use the parallel axis theorem regarding the common axis.
EXAMPLE 10.4.1
Determine the moments of inertia of the depicted area about the x and y axes shown. Hint: Use the formulas shown in Fig. 10.11 and the parallel axis theorem.
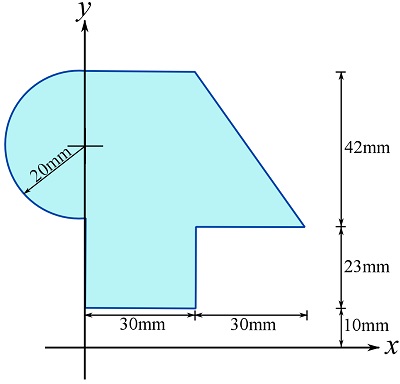
SOLUTION
Partition the area into simple disjoint shapes (areas) with known (or can be easily found) centroids. The location of centroids is needed as per the parallel axis theorem. One possible choice of sub-area is shown below. The centroids are determined using the information from Fig. 9.11.
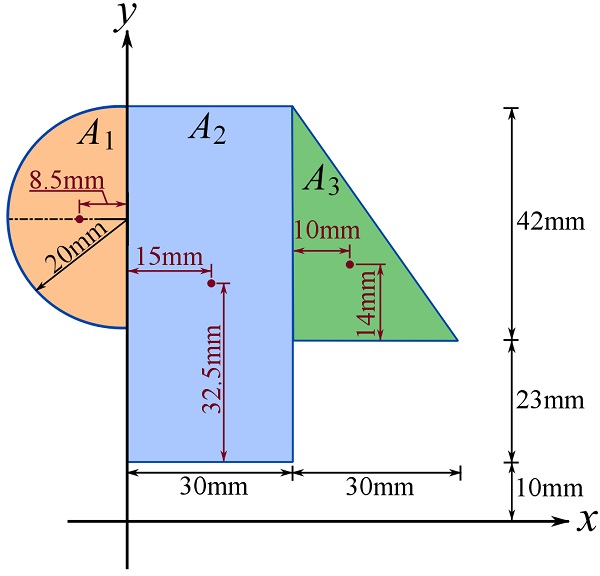
Part 1: moment of inertia about the x axis.
To calculate the moment of inertia, of ![]() about
about ![]() , we can use the parallel axes theorem. To this end, we need
, we can use the parallel axes theorem. To this end, we need ![]() being the moment of inertia of
being the moment of inertia of ![]() about the centroidal axis,
about the centroidal axis, ![]() , parallel to
, parallel to ![]() . The
. The ![]() axis and its distance to the
axis and its distance to the ![]() axis are shown in the figure below.
axis are shown in the figure below.
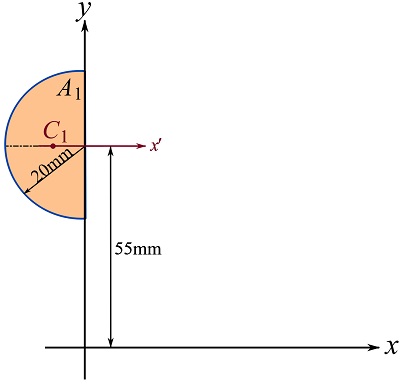
Letting ![]() be the moment of inertia of
be the moment of inertia of ![]() about the
about the ![]() , we can write,
, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}I_{1x} &= \bar I_{1x'} + Ad^2= \frac{1}{8}\pi r^4 + (\frac{1}{2}\pi r^2)d^2\\&= \frac{1}{8}\pi 20^4 + (\frac{1}{2}\pi 20^2)(55)^2 = 1.964\times 10^6\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6d6ca0eab68b85760d79c72dfb80d639_l3.png)
Similarly, area ![]() and the axis crossing its centroid and parallel to the
and the axis crossing its centroid and parallel to the ![]() axis are considered and shown as below.
axis are considered and shown as below.
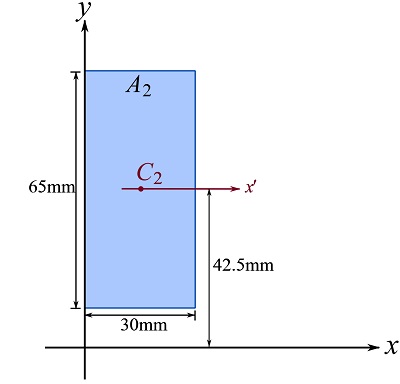
Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}I_{2x} &= \frac{1}{12}bh^3 + (bh)d^2\\&=\frac{1}{12}(30)(65)^3 + (30\times 65)(42.5)^2 = 4.209\times 10^6\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-102e6efd7370890365f3970fa98a510f_l3.png)
For area ![]() , we have the following configuration.
, we have the following configuration.
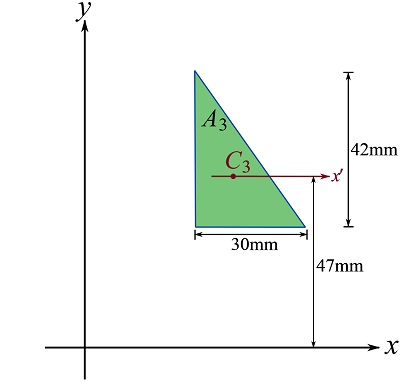
Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}I_{3x}&=\frac{1}{36}bh^3 + (\frac{1}{2}bh)d^2\\&= \frac{1}{36}(30)(42)^3 + (\frac{1}{2}30\times 42)(47)^2 = 1.453\times 10^6 \text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fba1147972fcabd95383437bcccd4083_l3.png)
Now, adding the moment of inertia of each part (about the common axis x) will give the moment of inertia of the whole area about the x axis as,
![]()
The above calculations can be summarized in a table as follows.
| sub-area | ||||
| 55 | ||||
| 32.5+10=42.5 | ||||
| 33+14=47 | ||||
Part 2: moment of inertia about the y axis.
To calculate ![]() of area
of area ![]() as shown below, we should note that the formula (
as shown below, we should note that the formula (![]() ) in Fig. 10.11 already expresses the moment of inertia of a semi-circular area about the axis along its base.
) in Fig. 10.11 already expresses the moment of inertia of a semi-circular area about the axis along its base.
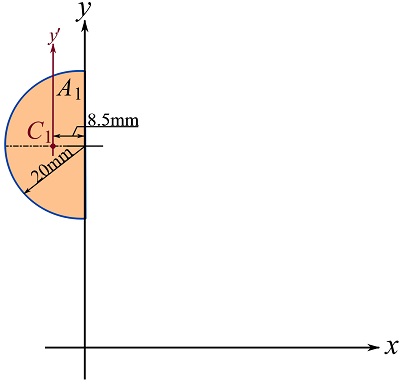
Therefore,
![]()
For area ![]() as shown, we should use the parallel axes theorem.
as shown, we should use the parallel axes theorem.
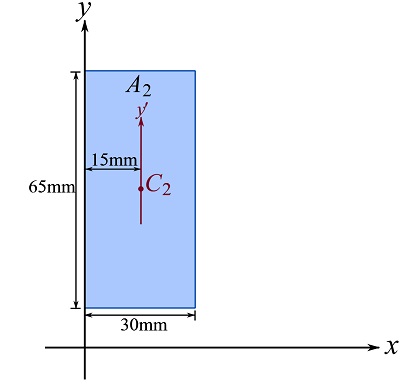
![Rendered by QuickLaTeX.com \[\begin{split}I_{2y}&= \frac{1}{12}bh^3 + (bh)d^2\\&= \frac{1}{12}(65)(30)^3 + (65\times 30)(15)^2 = 5.850\times 10^5\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ba984910103c405db1f7bd4b734b451d_l3.png)
And for ![]() ,
,
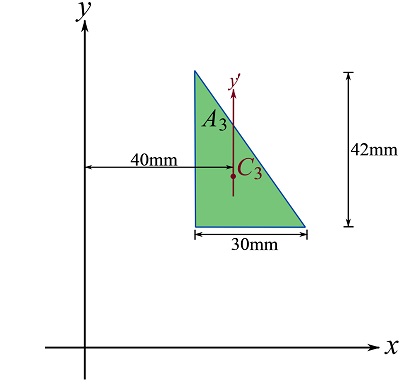
![Rendered by QuickLaTeX.com \[\begin{split}I_{3y}&=\frac{1}{36}bh^3 + (\frac{1}{2}bh)d^2\\&=\frac{1}{36}(42)(30)^3 + (\frac{1}{2}42\times 30)(40)^2 = 1.040\times 10^6\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-03677556393a8f4cbe7bb8e256f0f7e2_l3.png)
Consequently,
![]()
The above calculations can be summarized in a table as follows.
| sub-area | ||||
| * | * | * | ||
| 15 | ||||
| 30+10=40 | ||||
In many cases, the sub-areas are explicitly pronounced by the geometry of the area. The following example shows an instance.
EXAMPLE 10.4.2
For the displayed I-shaped cross-section of a beam, find the moments of inertia about the horizontal and vertical axes crossing the centroid of the area.
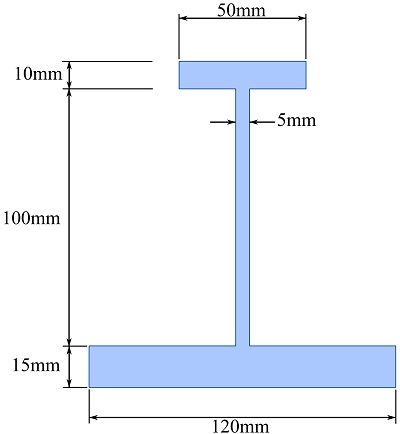
SOLUTION
Partition the area into disjoint sub-area and determine the centroid of the area.
The area can be partitioned into the sub-areas shown in the figure below. The centroid of each sub-area is determined and a Cartesian coordinate system is set to facilitate the calculation.
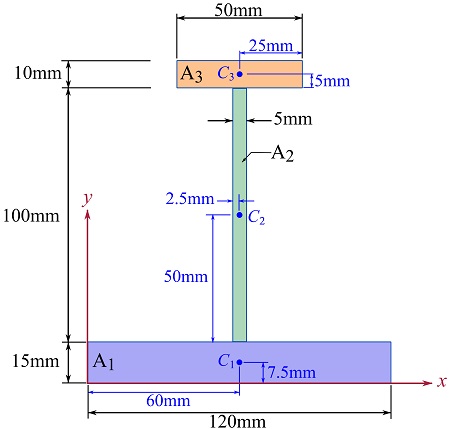
Although we can calculate it, we conclude, by the symmetry, that,
![]()
And,
![]()
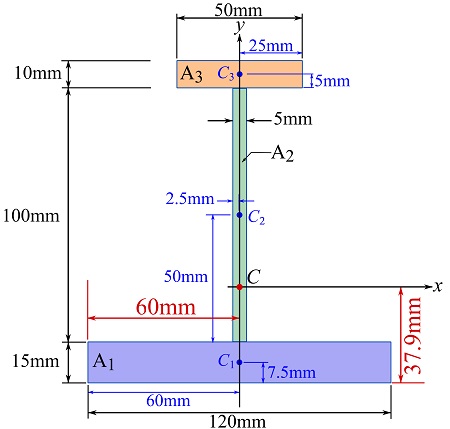
Follow the steps as shown in the previous example for each sub-area. The formula for calculating the moment of inertia of a rectangular area about a centroidal axis is ![]() as shown in Fig. 10.11.
as shown in Fig. 10.11.
Calculating ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split}I_x&= I_{1x}+I_{2x}+I_{3x}\\&=\frac{1}{12}(120)(15)^3+(120\times 15)(37.9-7.5)^2\\&+\frac{1}{12}(5)(100)^3+(5\times 100)(15+50-37.9)^2\\&+\frac{1}{12}(50)(10)^3+(50\times 10)(15+100+5-37.9)^2\\&= 5.855\times 10^6\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-97edc324c0ee584c62b9f8567375c41f_l3.png)
The calculations can also be tabulated as,
| sub-area | ||||
| (120)(15)=1800 | 37.9-7.5=30.4 | |||
| (5)(100)=500 | 15+50-37.9=27.1 | |||
| (50)(10)=500 | 15+100+5-37.9=82.1 | |||
Calculating ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split}I_y&= I_{1y}+I_{2y}+I_{3y}\\&=\frac{1}{12}(15)(120)^3\\&+\frac{1}{12}(100)(5)^3\\&+\frac{1}{12}(10)(50)^3\\&= 2.265\times 10^6\text{ mm}^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a54c20b3c93a6d5487f3289abdd1dc25_l3.png)
which can be tabulated as,
| sub-area | ||||
| (15)(120)=1800 | 0 | |||
| (100)(5)=500 | 0 | |||
| (10)(50)=500 | 0 | |||
The following interactive example demonstrates a beam cross section, its centroid and its moments of inertia about the axes (horizontal and vertical) crossing the centroid of the area. You can change the dimensions of each sub-area and also set the positions of the flanges (top parts) by horizontally dragging them. The purpose of this example is to let you observe the variations of the location of the centroid and the moments of inertia as you change the shape of the area. Nevertheless, it is recommended that you try to calculate some cases yourselves and check your answers. The unit of length, in the example, is arbitrary; you can assume milliliter.
Moment of inertia of an area with empty parts
As discussed in Section 9.3.5, an empty part (hollow region) of an area is treated as a negative area in the formulations. Consequently, an empty area has a negative value of moment of inertia.
EXAMPLE 10.4.3
Determine ![]() and
and ![]() of the beam cross sectional area about the x and y axes as shown.
of the beam cross sectional area about the x and y axes as shown.
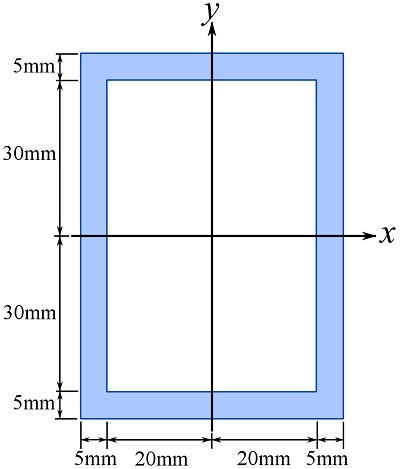
SOLUTION
As shown in the figure below, the area can be considered as the blue rectangular area (![]() ) minus the green rectangular area (
) minus the green rectangular area (![]() ).
).
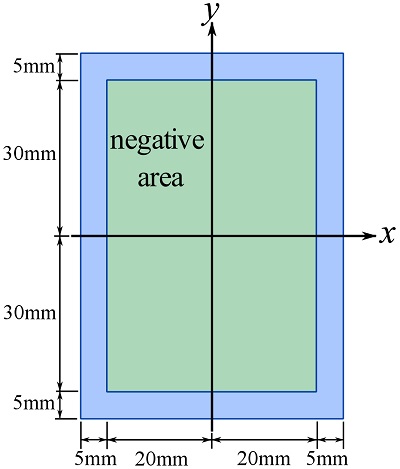
By symmetry, we recognize that the x and y axes are crossing the centroid of the rectangular areas. Therefore (using the formula in Fig. 10.11),
![]()
The calculations can be organized in a table as,
| sub-area | ||||
Blue area | (50)(70)=3500 | 0 | ||
Green area (negative | (40)(60)=2400 | 0 | ||
And,
![]()
which can be tabulated as,
| sub-area | ||||
Blue area | (70)(50)=3500 | 0 | ||
Green area (negative | (40)(60)=2400 | 0 | ||
Video
a https://www.engineeringintro.com/mechanics-of-structures/moment-of-inertia/moment-of-inertia-of-hollow-section/
