Vectors and their Operations: Vector operations using the parallelogram rule and trigonometry
The following are mathematical operations used for vectors in this course:
- Multiplication (or division) by a scalar.
- Vector addition (or subtraction).
- Vector products (dot product and cross product).
The first two operations are the fundamental operations and are presented below. Vector products are special functions and presented in Sections 2.7 and 2.8.
Multiplication (and division) of a vector by a scalar
A vector can be multiplied by a scalar and the result is another vector. A vector ![]() multiplied by a scalar
multiplied by a scalar ![]() will be equal the vector
will be equal the vector ![]() . This operation is denoted as
. This operation is denoted as ![]() . Division of a vector by a scalar
. Division of a vector by a scalar ![]() is the same as multiplication by
is the same as multiplication by ![]() . Multiplication of a vector by a scalar is implemented by the following rule:
. Multiplication of a vector by a scalar is implemented by the following rule:
If the scalar is a positive number, scalar multiplication simply scales the magnitude (length) of a vector. If the scalar is negative, the operation also reverses the direction of the vector.
Remark: multiplying a vector by a scalar scales the vector’s magnitude: if ![]() , then
, then ![]() in which
in which ![]() is the absolute value of the scalar
is the absolute value of the scalar ![]() .
.
Remark: for any non zero scalar ![]() , if
, if ![]() then
then ![]() scales and reverses (switches) the direction of
scales and reverses (switches) the direction of ![]() .
.
Remark: multiplication of any vector, ![]() , by zero results in the zero vector:
, by zero results in the zero vector: ![]() .
.
The following figure demonstrates different vectors as the results of multiplication of ![]() by a scalar.
by a scalar.

Click on the following interactive tool demonstrates ![]() multiplied by a scalar
multiplied by a scalar ![]() to produce a new vector
to produce a new vector ![]() . Move the slider to change the value of
. Move the slider to change the value of ![]() and notice the effect on the resulting red vector. When does the vector
and notice the effect on the resulting red vector. When does the vector ![]() reverse its direction?
reverse its direction?
Vector addition
The addition of vectors results in a new vector. For example, the addition of vectors ![]() and
and ![]() resulting in a vector
resulting in a vector ![]() is denoted as
is denoted as ![]() . There are two equivalent rules (laws) for vector addition: triangle rule, and parallelogram law.
. There are two equivalent rules (laws) for vector addition: triangle rule, and parallelogram law.
To calculate ![]() using the triangle rule follow these steps:
using the triangle rule follow these steps:
- Put
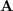 and
and  head to tail, and then,
head to tail, and then, - Close the triangle with the vector
 from the free tail to the free head of the vectors .
from the free tail to the free head of the vectors .
Fig. 2.5 demonstrates the triangle rule for vector addition.
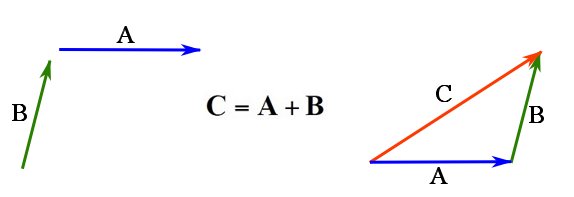
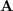 and
and  using the triangle rule.
using the triangle rule.The vector addition is commutative meaning ![]() . This can be readily observed in the following figure:
. This can be readily observed in the following figure:
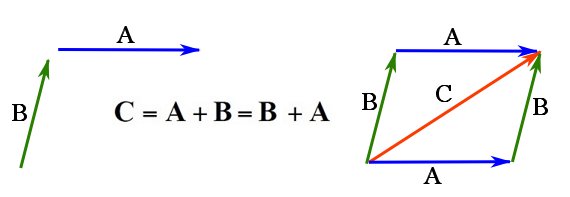
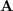 and
and  .
.To add two vectors using the parallelogram law, follow these steps:
- Bring the vectors to join at a point, say
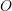 , by their tails.
, by their tails. - From the head of each vector draw a line parallel to the other vector. These two lines intersect at a point
 and form two adjacent lines of a parallelogram.
and form two adjacent lines of a parallelogram. - Draw a vector from point
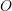 to the point
to the point  (the diagonal of the parallelogram). This vector is the resultant vector
(the diagonal of the parallelogram). This vector is the resultant vector 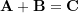 .
.
Figure 2.7 demonstrates vector addition using the parallelogram law.
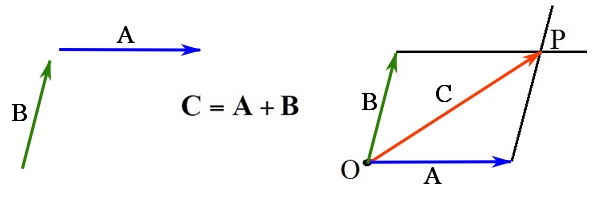
 and
and  using the parallelogram law.
using the parallelogram law.Vector subtraction. The difference between two vectors, or vector subtraction, follows the rules for vector addition. For two vectors ![]() and
and ![]() the operation
the operation ![]() can be written as
can be written as ![]() . An example is shown in Fig. 2.8.
. An example is shown in Fig. 2.8.
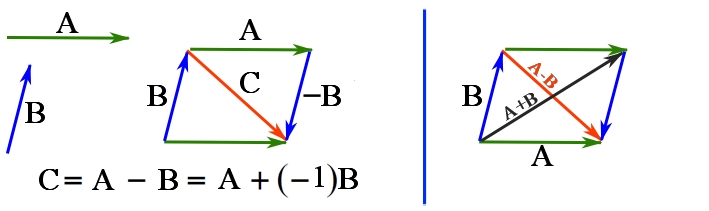
 and
and  using the parallelogram law.
using the parallelogram law.Remark: vector subtraction is not commutative because ![]() . In fact,
. In fact, ![]() .
.
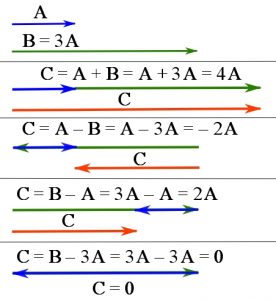
Addition (or subtraction) of parallel vectors. The addition (or subtraction) of parallel vectors is performed by bringing them head-to-tail and creating a longer or shorter vector. This means they are directly added (or subtracted) by their magnitudes.
Examples of vector addition (or subtraction) in the case of parallel vectors are demonstrated in Fig. 2.9.
Addition of several vectors. If more than two vectors are to be added (or subtracted), they will be added successively. For example ![]() . An example is as demonstrated below:
. An example is as demonstrated below:
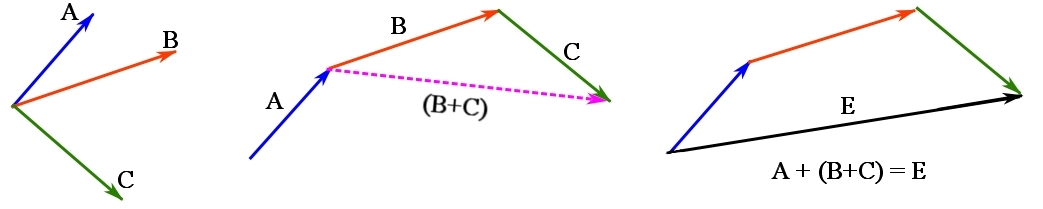
 ,
,  and
and  using the triangle rule.
using the triangle rule.Experiment with the following interactive tool to investigate the parallelogram law for vector addition.
Trigonometry for vector operations
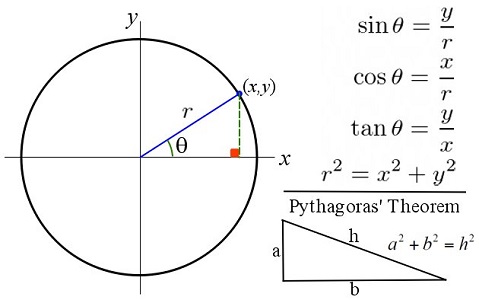
Trigonometric functions and laws are used to calculate the magnitude and direction of resultant vectors. The definition of the basic trigonometric functions are depicted in Fig. 2.11.
Based on the trigonometric functions, the Sine and Cosine laws hold for any triangle or any three vectors forming a triangle. Fig. 2.12 demonstrates the Sine and Cosine laws hold for a triangle and for three vectors forming a triangle. In the case of vectors, the laws applies on the magnitudes of the vectors.
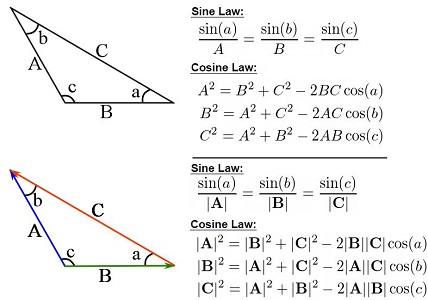
Remark: It should be understood that the magnitude of the resultant vector is not generally equal the addition of the magnitudes. In other words, ![]() . In fact,
. In fact, ![]() always holds. This statement, called the triangle inequality, can be explored or proved by using the Cosine law.
always holds. This statement, called the triangle inequality, can be explored or proved by using the Cosine law.
The following interactive tool illustrates the trigonometric functions. Use the slider to vary the angle ![]() of the arrow and notice the corresponding changes in
of the arrow and notice the corresponding changes in ![]() and
and ![]() .
. ![]() is the signed length of the green dotted line and
is the signed length of the green dotted line and ![]() is the signed length of the blue dotted line.
is the signed length of the blue dotted line.
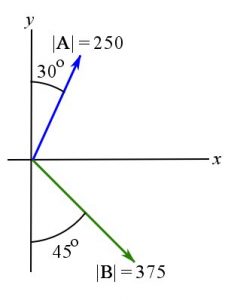
EXAMPLE 2.2.1
Determine the magnitude of the resultant vector ![]() and its direction measured clockwise from the positive x-axis shown.
and its direction measured clockwise from the positive x-axis shown.
SOLUTION
- Draw diagrams (parallelogram sides)
- Show known information on the diagrams
- Identify what to look for
Recall that Sine and Cosine Laws can be used to find angles and edge lengths, but more information is needed.
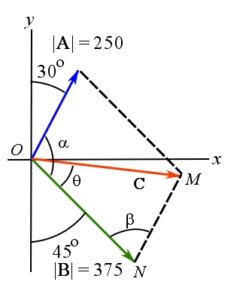
As a property of a parallelogram, ![]()
![]() +
+ ![]()
![]() =
= ![]()
Therefore, ![]()
For triangle ![]() ,
, ![]() (or
(or ![]() ) represents the resultant vector. From Cosine Law,
) represents the resultant vector. From Cosine Law,
![Rendered by QuickLaTeX.com \[\begin{split}OM^{2} &= ON^{2} + MN^{2} - 2(ON) (MN)( \cos{75^ {\circ}})\\&= 375^{2} + 250^{2} -(2)(375)(250) \cos{75^{\circ}}\\&\Rightarrow \ OM = 393.2 = |\bold C|\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-006e7eb70a54901b7ac6c9f3f47caaea_l3.png)
From Sine Law,
![Rendered by QuickLaTeX.com \[\begin{split}\frac{\sin{\theta}}{NM}&= \frac{\sin{75^{\circ}}}{OM}\\\frac{\sin{\theta}}{250}&= \frac{\sin{75^{\circ}}}{(393.2)}\\\angle \theta&= 37.89^{\circ}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-828db8827bb0ce4e06bfdefe449d1c92_l3.png)
The angle of ![]() with x axis is
with x axis is ![]() .
.
Videos
Vector Multiplication and Division by a Scalar:
Vector Addition using the Parallelogram Method:
