Forces and Moments: Simplification of force and couple systems
Resultant moment
Resultant moment of the moments of forces
Like forces (vectors), moments can be added together to determine their collective effect known as the resultant moment. Let ![]() be a system of forces acting on a body (Fig. 3.23). The resultant moment of the forces about a point
be a system of forces acting on a body (Fig. 3.23). The resultant moment of the forces about a point ![]() (anywhere in the space) is determined by a vector addition of the moment of each force about
(anywhere in the space) is determined by a vector addition of the moment of each force about ![]() ,
,
(3.23) ![]()
or in a concise notation,
![]()
where ![]() is the quasi-moment arm vector of
is the quasi-moment arm vector of ![]() , and
, and ![]() is the resultant moment about point
is the resultant moment about point ![]() .
.
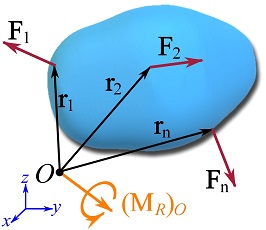
Remark: the resultant moment of forces is a moment acting about a point (or axis). This moment conveys the collective rotational tendencies of the forces about an specific point (or axis). Indeed, changing the location of the pivot point changes the resultant moment of the forces.
In the case of a coplanar (two-dimensional) force system, Eq. 3.23 reduces to an algebraic sum of the moments. In this case, the sign of the moments of the forces and their resultant follow the convention that associates a positive moment with a counterclockwise rotation.
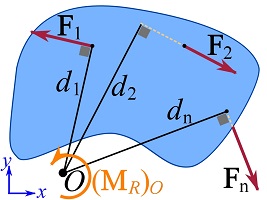
The resultant moment of a system of coplanar forces ![]() about a point
about a point ![]() in the plane of the forces (Fig. 3.24a) is,
in the plane of the forces (Fig. 3.24a) is,
(3.24) ![]()
where ![]() are the magnitude of the forces,
are the magnitude of the forces, ![]() are the moment arms, and the notation
are the moment arms, and the notation ![]() indicates the direction of positive moments. The result of the equation is a scalar. If
indicates the direction of positive moments. The result of the equation is a scalar. If ![]() is positive, the sense of the rotation of the moment is counterclockwise, otherwise it is clockwise.
is positive, the sense of the rotation of the moment is counterclockwise, otherwise it is clockwise.
In a Cartesian coordinate system, decomposing each force to its rectangular components and adding the moments of the components of the forces (according to the principle of moments) facilitate calculating the resultant moment.
EXAMPLE 3.4.1
Calculate the resultant moment of the force system about point ![]() .
.
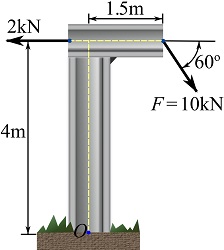
SOLUTION
Setting the positive directions (shown in the figure), the rectangular components of the forces are determined.
The sum of moments of the components of the forces about point ![]() is,
is,
![]()
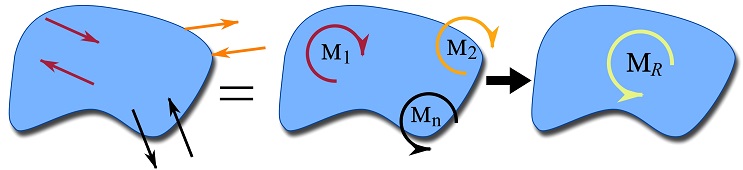
Resultant couple moment
If several couples (couples of forces) act on a body (Fig. 3.25), the couple moments can be added together to determine the resultant couple moment. Since the couple moments are free vectors (independent of location), their resultant is also a free vector. In a mathematical notation, the resultant of the couple moments ![]() is,
is,
(3.25) ![]()
where ![]() is the resultant couple moment. The calculation of a resultant couple moment does not depend on a pivot point, therefore
is the resultant couple moment. The calculation of a resultant couple moment does not depend on a pivot point, therefore ![]() has no subscription denoting a pivot point. Equation 3.25 is a vector sum in general, however, it becomes a scalar sum in two-dimensional problems. The sign of a couple moment in two-dimensions is positive if it is counterclockwise.
has no subscription denoting a pivot point. Equation 3.25 is a vector sum in general, however, it becomes a scalar sum in two-dimensional problems. The sign of a couple moment in two-dimensions is positive if it is counterclockwise.
Resultant Moment of a system of forces and couple moments
A system containing forces and couple moments acting on a body is referred to as a system of forces and couple moments or a force-couple system.
If forces ![]() and couple moments
and couple moments ![]() act on a body, the resultant moment of the forces and couple moments about a point
act on a body, the resultant moment of the forces and couple moments about a point ![]() is defined as the sum of the moments of the forces about
is defined as the sum of the moments of the forces about ![]() in addition to the sum of the couple moments. In a mathematical notation,
in addition to the sum of the couple moments. In a mathematical notation,
(3.26) ![]()
or in a concise notation,
![]()
This definition physically conveys the rotational tendencies produced by the forces about the pivot point ![]() plus the rotational tendencies of the couple moments produced on the body.
plus the rotational tendencies of the couple moments produced on the body.
and simplification of systems
A force-couple system can be reduced or simplified to an equivalent system that consists of only a resultant force and a resultant couple moment, or even a single force, applied at a specific point of the body (or space). The reduction of forces and moments simplifies the analysis of the system in question.
A simplified system makes it convenient to quickly observe and understand the overall disclosure of a force-couple system on the body. For example, each limb of a human body has its own weight, but it is convenient and more understandable (in many problems) to consider the total weight and shown it as a single force on the body rather than showing each limb’s weight. In this section, the concept of equivalent force-couple systems is first defined and then simplification of different force-couple systems are presented.
Equivalent systems
Two force-couple systems are called equivalent if their external effects on a rigid body are the same. The following two conditions needs to be satisfied.
1- The resultant forces of the two systems are equal, i.e.,
![]()
2- The resultant moments of the systems about any fixed arbitrary point, ![]() , in the space are equal, i.e.,
, in the space are equal, i.e.,
![]()
Note that the resultant moment of a system is the sum of moments produced by the system forces about a fixed point plus the couple moments.
Context: Simplification of force and couple systems
- Engineers often simplify systems by combining forces and moments to make calculations easier.
- When simplifying systems, engineers need to ensure that the simplified system has external effects equivalent to the original system.
- This approach is effective for determining support reactions as part of rigid body equilibrium (Section 5.2), particularly in structures subject to many combinations of point forces and/or structures subject to distributed loads (Section 3.5).
- This simplification approach is limited as it may not allow internal effects (e.g. tension, shear) in a member to be assessed. Internal effects are discussed more in Chapter 7 of this book.
Applications: Where do engineers use simplifications of force and couple systems?
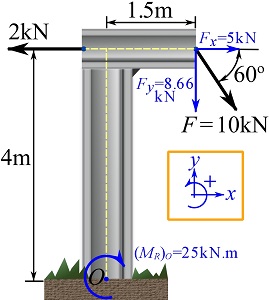
In addition to designing new structures, engineers also evaluate existing structures in case they are being changed to resist different types of loads or if they are degrading because of problems like corrosion. Looking at the column in Fig. 3.26, we see that forces are transferred into the column from a few sources including the steel beams resting on the column ledges (formally called ‘corbels’) as well as forces and moments coming from the above floor.
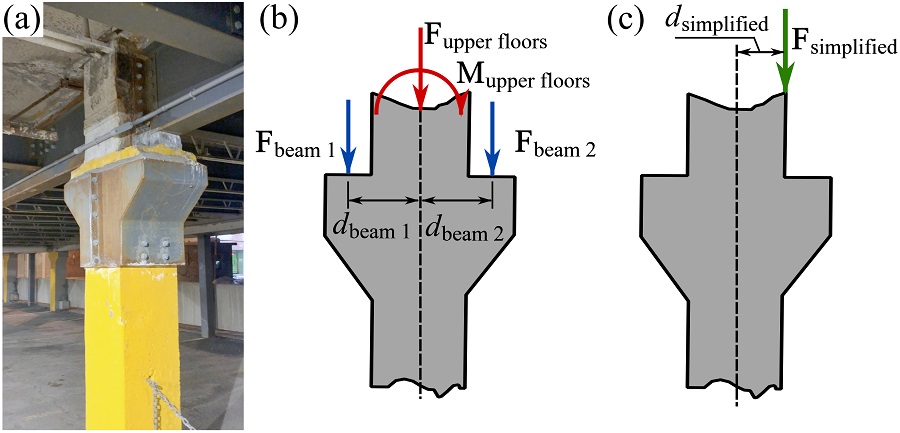
If you were to check this column’s adequacy at resisting the applied forces without failing the easiest approach is to reduce the system to a single force, ![]() , acting at an eccentricity,
, acting at an eccentricity, ![]() . With these simplified forces, you can compare these forces to the material capacity of the column accounting for the combination of forces and moments. Engineers often use design resources (e.g. tables and charts) that allow them to quickly evaluate the adequacy of these simplified systems. Material capacities and these design resources are discussed in upper year engineering courses.
. With these simplified forces, you can compare these forces to the material capacity of the column accounting for the combination of forces and moments. Engineers often use design resources (e.g. tables and charts) that allow them to quickly evaluate the adequacy of these simplified systems. Material capacities and these design resources are discussed in upper year engineering courses.
EXAMPLE 3.4.2
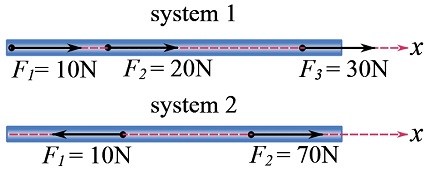
Consider two systems of non-equal but collinear forces (acting on the same bar) as shown in the figure. Show that both systems are equivalent.
Solution
1- The same resultant forces.
![Rendered by QuickLaTeX.com \[\begin{split}\text {system 1: } F_R&=\overset{+}{\rightarrow}\sum F_x= 10+20+30=60\text{ N}\\\text {system 2: } F_R&=\overset{+}{\rightarrow}\sum F_x= 70 -10=60\text{ N}\\\therefore \underset{\text{System 1}}{\bold F_R}&=\underset{\text{System 2}}{\bold F_R}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6e600e48483b6c449b920bbd484fc4d6_l3.png)
2- The same resultant moments.
Selecting a point on the line of action of the forces leads to zero resultant moments for both systems.
Therefore the two force-couple systems are equivalent.
EXAMPLE 3.4.3
Prove that the coplanar force-couple systems shown in the figure are equivalent.

1- The same resultant forces.
![Rendered by QuickLaTeX.com \[\begin{split}\text {system 1: } F_R&=+\uparrow\sum F_y= -1 -1=-2 \implies F_R=2 \text{ N}\downarrow\\\text {system 2: } F_R&=+\uparrow\sum F_y= -2 \implies F_R=2 \text{ N}\downarrow\\\therefore \underset{\text{System 1}}{\bold F_R}&=\underset{\text{System 2}}{\bold F_R}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8eb11a6846c979e32807a44dc000349c_l3.png)
2- The same resultant moments.
The resultant moments of both systems about an arbitrary point should be equal. We choose point ![]() on right end of the bar and calculate the resultant moments.
on right end of the bar and calculate the resultant moments.
![Rendered by QuickLaTeX.com \[\begin{split}\text {system 1: } (M_R)_O&= \circlearrowleft{+}\sum Fd= -(1)(4) -(1)(6) = -10\text { N.m}\\\implies (M_R)_O&=10\text { N.m}\circlearrowright\\\text {system 2: } (M_R)_O&= \circlearrowleft{+}\sum Fd + \sum M= (2)(0) -10 = -10\text { N.m}\\\implies (M_R)_O&=10\text { N.m}\circlearrowright\\\therefore \underset{\text{System 1}}{(\bold M_R)_O}&=\underset{\text{System 2}}{(\bold M_R)_O}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-06606632650377654d78b535c6568418_l3.png)
Therefore the systems are equivalent.
In the last example, we observe that a system of two forces is equivalently represented by a system of one force and a couple moment. Any system can be simplified to a system including only a force and a couple. This concept is presented in the next subsection.
The concept of equivalent systems can be used to simplify or reduce a force-couple system to an equivalent system that generally includes only a resultant force and a resultant couple moment at one specific point. This process is called the simplification of a force-couple system.
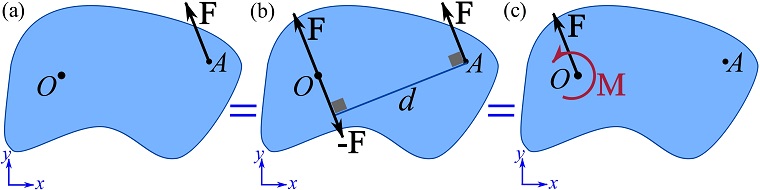
The following example shows how to move a force to a different application point without changing its external effect on the same rigid body. Consider a force ![]() in the x-y plane as shown in Fig 3.27a. The force is acting at point
in the x-y plane as shown in Fig 3.27a. The force is acting at point ![]() . We intend to find an equivalent system in which
. We intend to find an equivalent system in which ![]() acts at (or relocated to) point
acts at (or relocated to) point ![]() .
.
We can add (place) both ![]() and
and ![]() to the at point
to the at point ![]() without changing the original system (Fig. 3.27b); because
without changing the original system (Fig. 3.27b); because ![]() . The system of forces shown in Fig. 3.27b indicates that
. The system of forces shown in Fig. 3.27b indicates that ![]() at
at ![]() and
and ![]() at
at ![]() form a couple and can be replaced by a couple moment with the magnitude
form a couple and can be replaced by a couple moment with the magnitude ![]() . The couple moment is a free vector and can be placed anywhere; we choose to locate it at point
. The couple moment is a free vector and can be placed anywhere; we choose to locate it at point ![]() (Fig. 3.27c). The resultant system as shown in Fig. 3.27c is an equivalent system consisting of a force and a couple moment.
(Fig. 3.27c). The resultant system as shown in Fig. 3.27c is an equivalent system consisting of a force and a couple moment.
Upon relocating ![]() , the added couple moment with the magnitude
, the added couple moment with the magnitude ![]() is added (Fig. 3.27c). This states that if a force is relocated from point
is added (Fig. 3.27c). This states that if a force is relocated from point ![]() to point
to point ![]() (not on the line of action of the force), a couple moment
(not on the line of action of the force), a couple moment ![]() should be added to the equivalent system to preserve the moment that the force in the original system creates about point
should be added to the equivalent system to preserve the moment that the force in the original system creates about point ![]() .
.
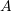 to point
to point 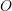 .
.The general procedure of the simplification of a force-couple system to an equivalent system has the following steps:
- Choose a point,
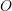 , on the body (or in the space) for all forces to be relocated there.
, on the body (or in the space) for all forces to be relocated there. - Calculate the resultant moment of the forces about point
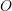 and the couple moments, i.e.
and the couple moments, i.e. 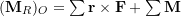 .
. - Move all the forces to the new location (
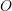 ) and calculate the resultant force
) and calculate the resultant force 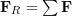 .
. - Place, at
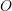 , a couple moment
, a couple moment 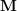 equal to
equal to 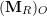 .
.
Remark: to relocate a force ![]() from point
from point ![]() to a new point
to a new point ![]() , whenever visualization of forces are convenient (like in coplanar systems), you can first show the forces
, whenever visualization of forces are convenient (like in coplanar systems), you can first show the forces ![]() and
and ![]() at point
at point ![]() . Then, create a couple moment using
. Then, create a couple moment using ![]() at
at ![]() and
and ![]() at
at ![]() , and show the couple moment together with
, and show the couple moment together with ![]() at
at ![]() .
.
EXAMPLE 3.4.4
Reduce (simplify) the following system to an equivalent system consisting of a force and a couple moment acting at point ![]() .
.
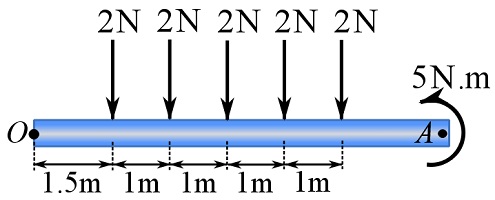
The following steps are take.
1- Calculate the resultant moment of the forces about point ![]() and the couple moments, i.e.
and the couple moments, i.e. ![]() (scalar formulation in two dimensions).
(scalar formulation in two dimensions).
![]()
The negative sign of ![]() means the resultant moment is clockwise. Therefore,
means the resultant moment is clockwise. Therefore,
![]()
2- Calculate the resultant force ![]() (scalar formulation in two dimensions).
(scalar formulation in two dimensions).
![]()
3- Place, at ![]() , the resultant force
, the resultant force ![]() and a couple moment
and a couple moment ![]() equal to
equal to ![]() .
.

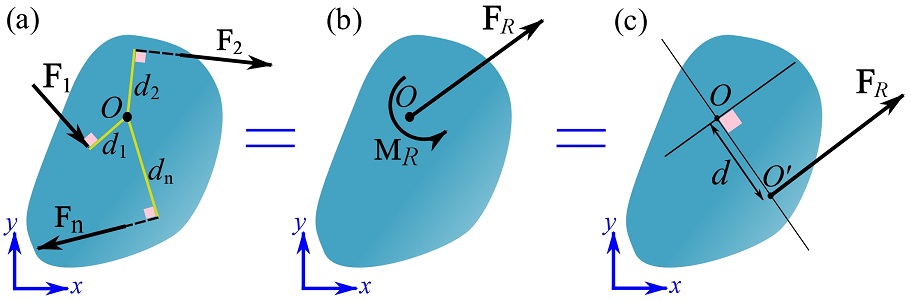
Although all systems can be reduced to an equivalent system consisting of a force and a couple moment, there are systems that can be further reduced to a single resultant force or a wrench as presented below.
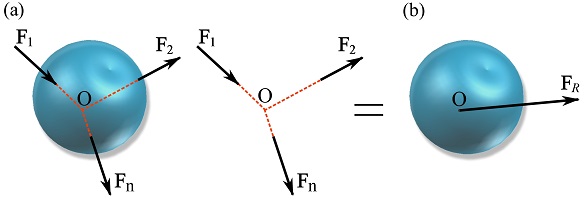
1- Concurrent force systems
In a concurrent force system (Fig. 3.28a), the lines of action of the forces meet (intersect) at a common point ![]() . Therefore, the forces produce no moment about
. Therefore, the forces produce no moment about ![]() and the system can be reduced to an equivalent system consisting of one resultant force
and the system can be reduced to an equivalent system consisting of one resultant force ![]() as shown in Fig. 3.28b.
as shown in Fig. 3.28b.
2- Coplanar force systems
In a coplanar force system (Fig. 3.29a), the lines of action of the forces are in the same plane, say x-y plane. The moments of the forces about any point on the plane are perpendicular to the plane, so are their resultant moment. This system can be initially reduced to a resultant force ![]() located at any point
located at any point ![]() and a resultant couple moment,
and a resultant couple moment, ![]() of the forces about point
of the forces about point ![]() (Fig. 3.29b).
(Fig. 3.29b).
Then, the system can be further simplified to a system that contains only ![]() as shown in Fig. 3.29c. This is achieved by offsetting in the plane
as shown in Fig. 3.29c. This is achieved by offsetting in the plane ![]() by distance
by distance ![]() from
from ![]() (Fig 3.29c). Offsetting the force can replicate the same moment,
(Fig 3.29c). Offsetting the force can replicate the same moment, ![]() , about point
, about point ![]() . This leads to a further simplified system shown in Fig. 3.29c.
. This leads to a further simplified system shown in Fig. 3.29c.
To find ![]() , the resultant moments of the systems shown in Fig. 3.29b and c must be equal. Choosing point
, the resultant moments of the systems shown in Fig. 3.29b and c must be equal. Choosing point ![]() and using the scalar formulation, we write,
and using the scalar formulation, we write,
![Rendered by QuickLaTeX.com \[\begin{split}\underset{\text{System b}}{(M_R)_O}&=\underset{\text{System c}}{( M_R)_O}\implies M_R = F_Rd\\\therefore d&=\frac{M_R}{F_R}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b93b0512586d7b27f3b3cb9d94eb26cb_l3.png)
It should be noted that ![]() should be offset in the correct side of
should be offset in the correct side of ![]() , in order to replicate the couple moment (
, in order to replicate the couple moment (![]() ). This means that
). This means that ![]() at its final location,
at its final location, ![]() , should create a moment that is equal to
, should create a moment that is equal to ![]() about
about ![]() .
.
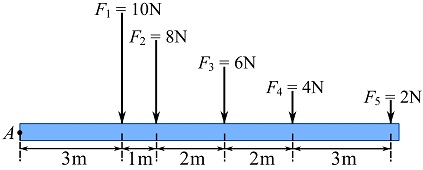
EXAMPLE 3.4.5
Reduce (simplify) the system of coplanar forces to a system consisting of a single resultant force. Measured from point ![]() , determine
, determine ![]() , the location of the resultant force.
, the location of the resultant force.
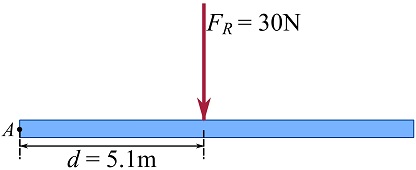
SOLUTION
1- Calculate ![]() .
.
![]()
2- Make the resultant moments of the original and the simplified systems equal.
![]()
The negative sign of ![]() means the resultant moment is clockwise. Therefore, the downward resultant force should be right to the rotation point to replicate such a moment. Therefore,
means the resultant moment is clockwise. Therefore, the downward resultant force should be right to the rotation point to replicate such a moment. Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}\text {Original system } (M_R)_A&= 152\text { N.m} \circlearrowright\\\text {Simplified system } (M_R)_A&= \circlearrowleft{+} F_Rd= -(30)(d)\text { N.m}\\&\implies F_Rd= (30)(d)\text { N.m}\circlearrowright\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d164fc6cd32591143518943ada49a5e3_l3.png)
Letting ![]() leads to,
leads to,
![]()
3- Parallel force systems (non-coplanar)
A parallel force system contains forces that are parallel to each other, say along the ![]() axis as shown in Fig. 3.30a. Parallel forces can be slid to a common perpendicular plane like the x-y plane in this case (Fig 3.30a). A system of parallel forces can be initially simplified to a system consisting of a resultant force
axis as shown in Fig. 3.30a. Parallel forces can be slid to a common perpendicular plane like the x-y plane in this case (Fig 3.30a). A system of parallel forces can be initially simplified to a system consisting of a resultant force ![]() applied at a point
applied at a point ![]() in the x-y plane, and a resultant couple moment
in the x-y plane, and a resultant couple moment ![]() as shown in Fig. 3.30b.
as shown in Fig. 3.30b.
Since all forces are parallel, ![]() is parallel to the
is parallel to the ![]() axis. Also, all moments of the forces are perpendicular to the axis
axis. Also, all moments of the forces are perpendicular to the axis ![]() and therefore
and therefore ![]() is perpendicular to the resultant force.
is perpendicular to the resultant force.
Similar to the further simplification of a coplanar system, where ![]() and
and ![]() are perpendicular, a system of parallel forces can be further reduced to a single resultant force (Fig. 3.30c). To achieve this,
are perpendicular, a system of parallel forces can be further reduced to a single resultant force (Fig. 3.30c). To achieve this, ![]() should be offset (to point
should be offset (to point ![]() ) in the plane containing
) in the plane containing ![]() and perpendicular to the axis of
and perpendicular to the axis of ![]() as shown in Fig 3.30c. The offset distance
as shown in Fig 3.30c. The offset distance ![]() from
from ![]() is determined as,
is determined as,
![]()
where ![]() and
and ![]() . It should be noted that the
. It should be noted that the ![]() should be offset in the correct side of
should be offset in the correct side of ![]() in order to replicate
in order to replicate ![]() about
about ![]() .
.

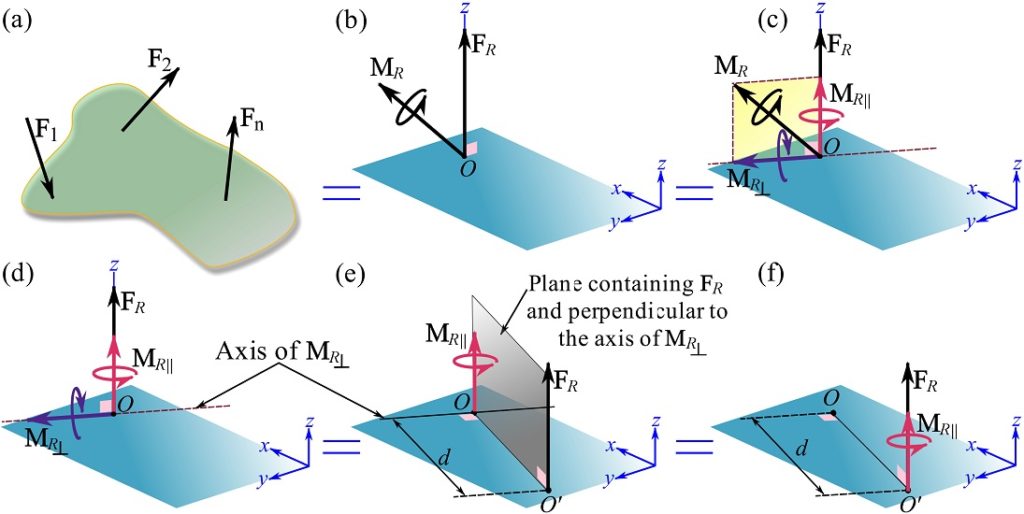
4- Systems reducing to a wrench
A general force-couple system in three dimensions (Fig. 3.31a) can be reduced to an equivalent system (Fig. 3.31b) consisting of a resultant force ![]() at a point
at a point ![]() and a resultant couple moment
and a resultant couple moment ![]() .
.
Since ![]() and
and ![]() are not generally perpendicular to each other (as in a case of a parallel force system), the system cannot be further reduced to a single resultant force. However, this system can be further simplified to an equivalent system called a wrench. To achieve this,
are not generally perpendicular to each other (as in a case of a parallel force system), the system cannot be further reduced to a single resultant force. However, this system can be further simplified to an equivalent system called a wrench. To achieve this, ![]() is resolved into components parallel and perpendicular to the resultant force
is resolved into components parallel and perpendicular to the resultant force ![]() . The components of
. The components of ![]() are shown in Fig. 3.31c.
are shown in Fig. 3.31c.
The parallel component (![]() ) and perpendicular component (
) and perpendicular component (![]() ) of
) of ![]() can be obtained using the dot product as (see Section 2.6.4),
can be obtained using the dot product as (see Section 2.6.4),
![]()
where ![]() is the unit vector of
is the unit vector of ![]() .
.
For the purpose of clear visualization, ![]() and the components of
and the components of ![]() are demonstrated in Fig. 3.31d.
are demonstrated in Fig. 3.31d.
Since ![]() and
and ![]() are perpendicular to each other, offsetting
are perpendicular to each other, offsetting ![]() in the plane containing
in the plane containing ![]() and perpendicular to
and perpendicular to ![]() can replicate
can replicate ![]() . As demonstrate in Fig 3.31e, offsetting
. As demonstrate in Fig 3.31e, offsetting ![]() to point
to point ![]() by distance
by distance ![]() , where
, where ![]() and
and ![]() , reduces the system to
, reduces the system to ![]() and
and ![]() as shown in Fig. 3.31f.
as shown in Fig. 3.31f.
This final reduced system is called a wrench or screw as it resembles screwing which needs a simultaneous use of force and couple moment.
Videos
Force Reduction – Moment Couple System;
Force Reduction – Single Force Without Moment:
Force Reduction – Wrench:
