Moments of Inertia of area: Polar moment of inertia
When an object is being twisted about an axis, we would like to know its stiffness against twisting. One of the quantities that reflects this stiffness is called the polar moment of inertia of the cross section, which is perpendicular to the axis. Similar to the concept of rectangular moment of inertia, the polar moment of inertia of an area is another geometric property of the area. The difference is that axis of rotation (the pole) is perpendicular to the area, instead of being in the same plane of the area as the case for the rectangular moment of inertia. The polar moment of inertia of an area is defined as the moment of inertia about a point (the interaction of the area and the axis of rotation). Consider an area ![]() and a point
and a point ![]() in the plane of the area as shown in Fig. 10.6.
in the plane of the area as shown in Fig. 10.6.
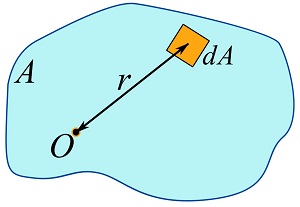
If ![]() is the distance from
is the distance from ![]() to a rectangular differential area,
to a rectangular differential area, ![]() , shown in Fig. 10.6, then the polar moment of inertia of the area is defined as,
, shown in Fig. 10.6, then the polar moment of inertia of the area is defined as,
(10.5) ![]()
Note that ![]() does not need to be a point within the area.
does not need to be a point within the area.
In a Cartesian coordinate system with an origin ![]() as shown in Fig. 10.7,
as shown in Fig. 10.7, ![]() (by Pythagoras’ theorem).
(by Pythagoras’ theorem).
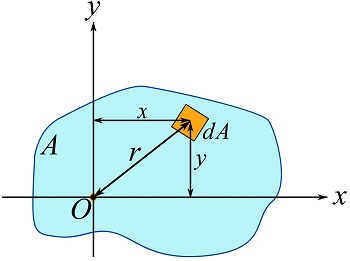
Consequently, Eq. 10.5 can be written as,
(10.6) ![]()
Both Eqs. 10.5 and 10.6 can be recruited to calculate ![]() . The approach should be chosen based on the problems.
. The approach should be chosen based on the problems.
EXAMPLE 10.2.1
Determine the polar moment of inertia of a circular area about its center.
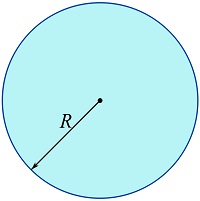
SOLUTION
Approach 1:
Consider the origin set at the center of the circular area. The geometry of the area allows us to choose an annular, i.e. ring-shape, differential element as shown in the figure below for the integration. The distance from any place on the element to the origin of the coordinate system (the center of the area in this case) is equal to ![]() . Note that
. Note that ![]() is a variable and its value changes according to the position of the differential ring. The area of the differential element is
is a variable and its value changes according to the position of the differential ring. The area of the differential element is ![]() .
.
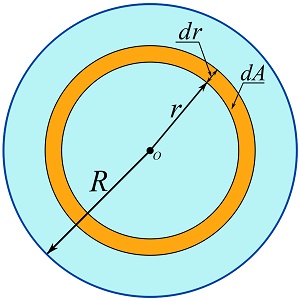
Therefore, by Eq. 10.5, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}J_O &= \int_A r^2dA=\int_0^R (r^2) 2\pi r dr\\&=\frac{\pi R^4}{2}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6f613100bfee8374d94cc74b47798096_l3.png)
Approach 2:
Set a Cartesian coordinate system with the origin located at the center of the circle as shown and use Eq. 10.6 and the results from Example 10.1.4 expressing ![]() for a circle with a radius of
for a circle with a radius of ![]() .
.
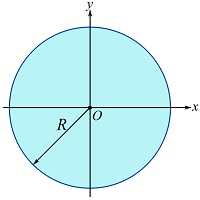
Therefore,
![]()
As demonstrated in the following example, calculating the polar moment of inertia of a rectangular area about its center (centroid) is a problem that can be solved much easier using Eq. 10.6 (in a Cartesian coordinate system) than using the polar formulation, Eq. 10.5.
EXAMPLE 10.2.2
Determine the polar moment of inertia of a rectangular area about its center (denoted as ![]() in the figure). Use the results of Example 10.1.1 expressing
in the figure). Use the results of Example 10.1.1 expressing ![]() and
and ![]() .
.
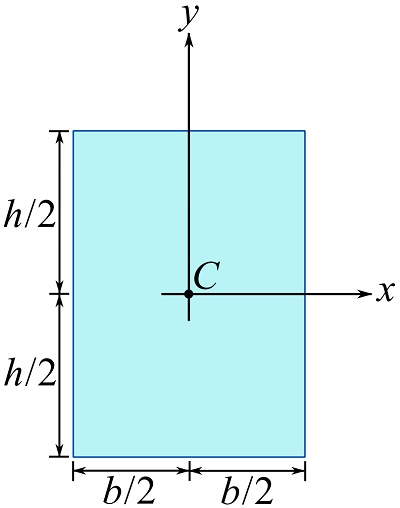
SOLUTION
![]()
A physical application of the polar moment of inertia of an area: torsional stiffness
Consider a circular shaft fixed (welded to a fixed plate) at one end as shown in Fig. 10.8. It is tangible that twisting the shaft (to a certain degree of rotation) about its central axis (denoted as x) requires a larger twisting moment for a shaft having a larger radius.
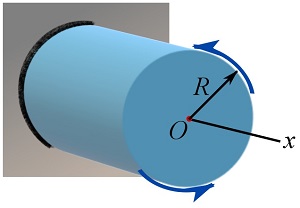
The quantity that describes how difficult to twist a body about its central axis is called the torsional stiffness, which is directly related to the polar moment(s) of inertia of the cross section(s) of the body.
EXAMPLE 10.2.3
Consider two shafts fixed at one of their ends as shown in the figure. The shafts have the same length, and their cross-sectional areas are equal; this means that each shaft can be made out of the other one by redistributing the material. Which shaft’s cross section has a larger polar moment of inertia, i.e. harder to twist?
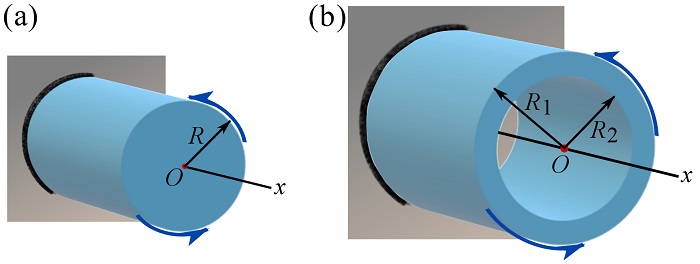
SOLUTION
Calculate ![]() for the section of each shaft. Follow the solution of Example 10.2.1
for the section of each shaft. Follow the solution of Example 10.2.1
For the shaft in Figure (a):
![]()
For the shaft in Figure (b):
![Rendered by QuickLaTeX.com \[\begin{split}J_O &= \int_A r^2dA=\int_{R_2}^{R_1} (r^2) 2\pi r dr\\&=\frac{\pi}{2}(R_1^4-R_2^4)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2c022bdd5fe5a4d10599f1bd719c87a7_l3.png)
Since the shafts have equal cross-sectional area, we can write,
![]()
On the other hand, ![]() because
because ![]() . Therefore, we can write,
. Therefore, we can write,
![Rendered by QuickLaTeX.com \[\begin{split}(R_1^4-R_2^4)&=(R_1^2-R_2^2)(R_1^2+R_2^2)=R^2(R_1^2+R_2^2)>(R^2)(R^2)\\&\implies \frac{\pi}{2}(R_1^4-R_2^4)>\frac{\pi}{2}R^4\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-da08304492858da15684509d09172c6c_l3.png)
meaning that the cross section of the hollow shaft has a larger polar moment of inertia (about its center) and hence relatively more difficult to twist.
