Vectors and their Operations: Cross product
The cross product and its properties
The cross product of two vectors is an operation that takes two vectors ![]() and
and ![]() and returns a vector
and returns a vector ![]() . This operation is denoted by
. This operation is denoted by ![]() and is read “C equals A cross B”. The magnitude of
and is read “C equals A cross B”. The magnitude of ![]() is defined as,
is defined as,
(2.22) ![]()
in which ![]() is the angle between the two vectors.
is the angle between the two vectors.
The definition of the magnitude of the cross product implies that, ![]() if two non-zero vectors are parallel.
if two non-zero vectors are parallel.
By definition, ![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() , which are not parallel, and its sense of direction is specified by the right-hand rule. In other words,
, which are not parallel, and its sense of direction is specified by the right-hand rule. In other words, ![]() is perpendicular to the plane containing the non-parallel vectors
is perpendicular to the plane containing the non-parallel vectors ![]() and
and ![]() such that
such that ![]() (or
(or ![]() ) is in the direction of the thumb following the right-hand rule (Fig. 2.26a). The right-hand rule can also be equivalently demonstrated by the right-hand three-finger rule as demonstrated in Fig. 2.26b.
) is in the direction of the thumb following the right-hand rule (Fig. 2.26a). The right-hand rule can also be equivalently demonstrated by the right-hand three-finger rule as demonstrated in Fig. 2.26b.
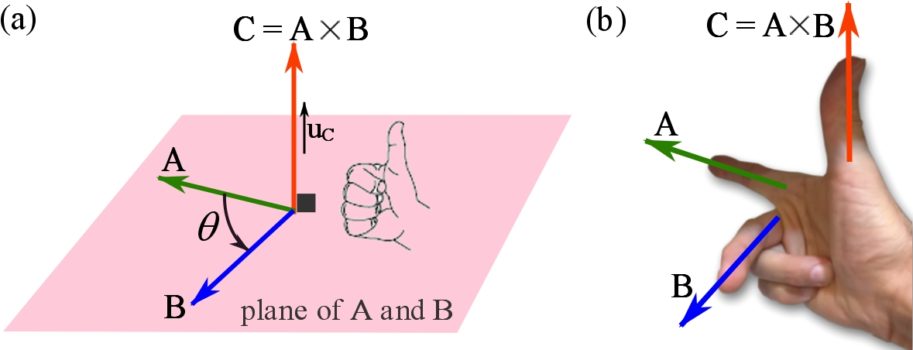
If ![]() is the unit vector of
is the unit vector of ![]() , the resultant of a cross product
, the resultant of a cross product ![]() can be written as,
can be written as,
(2.23) ![]()
The following interactive tool illustrates ![]() . Use the sliders to change the angles of
. Use the sliders to change the angles of ![]() and
and ![]() with the Cartesian axes, and observe the resultant of their cross product.
with the Cartesian axes, and observe the resultant of their cross product.
Properties of Cross product
- Anti-commutativity:
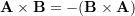
- Associativity: for
 being a scalar,
being a scalar, 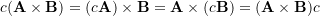
- Distributivity:
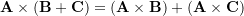
Cross product in CVN
In a Cartesian frame the following relationships are readily obtained for the mutually perpendicular unit vectors ![]() ,
, ![]() and
and ![]() .
.
(2.24) ![Rendered by QuickLaTeX.com \[ \begin{matrix} \bold i\times \bold i=\bold 0 &\bold i\times \bold j=\bold k & \bold i\times \bold k=-\bold j \\ \bold j\times \bold i=-\bold k & \bold j\times \bold j=\bold 0 & \bold j\times \bold k=\bold i \\ \bold k\times \bold i=\bold j & \bold k\times \bold j=-\bold i & \bold k\times \bold k=\bold 0 \end{matrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-14b8530a57bbaf2b85b6afc467425e0c_l3.png)
Based on the above results and the properties of the cross product, the cross product of two vectors in their CVN is,
![Rendered by QuickLaTeX.com \[ \begin{split} \bold A&=A_x\bold i + A_y\bold j+A_z\bold k\quad , \quad \bold B=B_x\bold i+B_y\bold j+B_z\bold k\\\bold C = \bold A\times \bold B&=(A_xB_x)\bold i\times \bold i +(A_xB_y)\bold i\times \bold j +(A_xB_z)\bold i\times \bold k\\&+(A_yB_x)\bold j\times \bold i +(A_yB_y)\bold j\times \bold j +(A_yB_z)\bold j\times \bold k \\&+(A_zB_x)\bold k\times \bold i +(A_zB_y)\bold k\times \bold j +(A_zB_z)\bold k\times \bold k \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-06c212c9e16c04abaa6d0c318e9dd3b3_l3.png)
leading to,
(2.25) ![]()
This result need not to be memorized and can be obtained by calculating the following determinant symbolically.
(2.26) ![Rendered by QuickLaTeX.com \[\bold A\times\bold B = \left\|\begin{matrix} \bold i & \bold j & \bold k \\ A_x & A_y & A_z \\ B_x & B_y & B_z \\ \end{matrix}\right\|\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1335c22037e5eba4719310eb1b70ef71_l3.png)
As a reminder, the determinant of a two-by-two matrix ![]() is a scalar defined as,
is a scalar defined as,
![]()
Consequently, the determinant of a three-by-three matrix ![]() is a scalar defined as
is a scalar defined as
![Rendered by QuickLaTeX.com \[M=\begin{bmatrix}a && b && c\\ d && e && f \\ g && h && i\end{bmatrix}\implies\|M\|=a\left\|\begin{matrix} e & f \\ h & i \end{matrix}\right\| - b\left\|\begin{matrix} d & f \\ g & i \end{matrix}\right\| + c\left\|\begin{matrix} d & e \\ g & h \end{matrix}\right\|\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-251157da36dda50196edd8fc9993592d_l3.png)
The following tool calculates the cross product ![]() . The vector
. The vector ![]() is drawn in green.
is drawn in green.
