Problems: Chapter 8
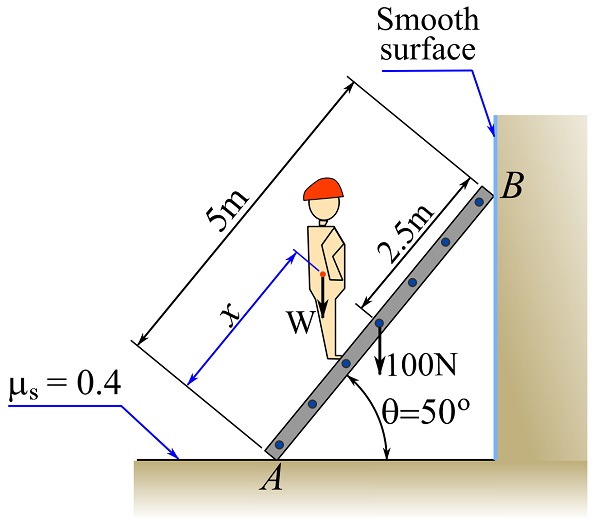
1- A ladder, on which a person is standing, is leaning against the wall as shown. The floor has a coefficient of static friction as ![]() , and the wall can be assumed frictionless (smooth) as it is covered by smooth tiles. The weight of the ladder acting at its center of gravity (the middle point of the length of the ladder) is
, and the wall can be assumed frictionless (smooth) as it is covered by smooth tiles. The weight of the ladder acting at its center of gravity (the middle point of the length of the ladder) is ![]() . The weight of the person is the person is
. The weight of the person is the person is ![]() and its location along the ladder is denoted as
and its location along the ladder is denoted as ![]() measured from point
measured from point ![]() shown in the figure. Determine how far the person can (slowly and with no acceleration) clime the ladder before the ladder slides. Hint: determine
shown in the figure. Determine how far the person can (slowly and with no acceleration) clime the ladder before the ladder slides. Hint: determine ![]() if the ladder is about to slide (impending motion).
if the ladder is about to slide (impending motion).
ANSWER
![]()
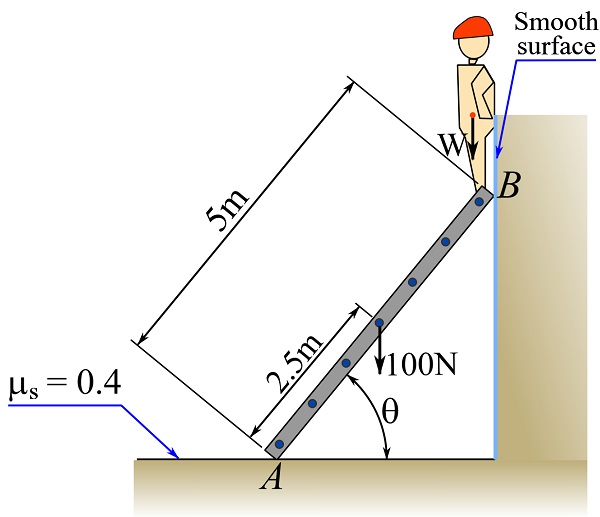
2- With the constant assumptions of Problem 1, what should be the minimum inclination angle, ![]() of the ladder so that the person can reach and stand on the top of the ladder as shown?
of the ladder so that the person can reach and stand on the top of the ladder as shown?
ANSWER
![]()
Note that
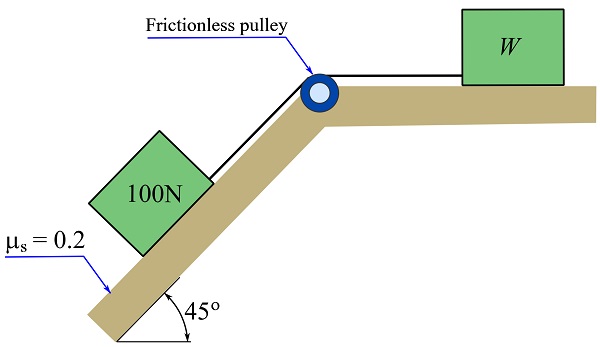
3- Determine the minimum weight, ![]() , of the box on the horizontal surface so that the boxes stay stationary as shown.
, of the box on the horizontal surface so that the boxes stay stationary as shown.
ANSWER
![]()
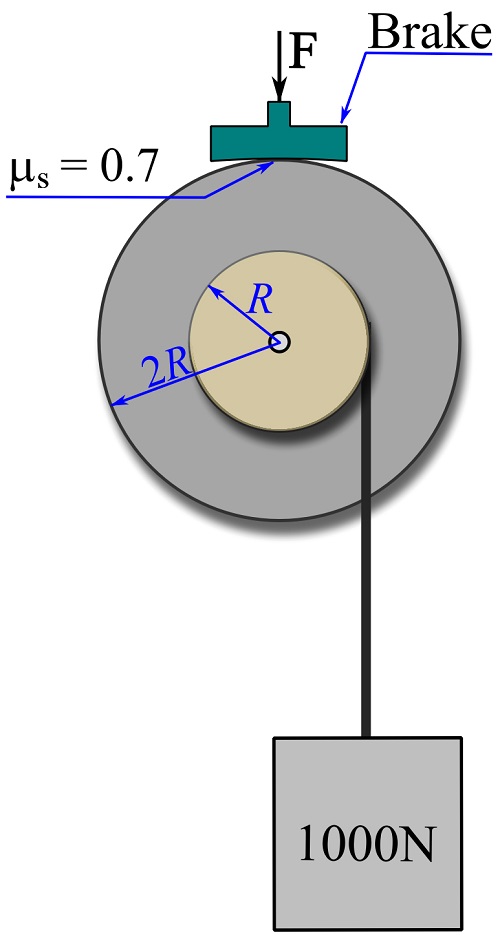
4- The spool, shown in the figure, is holding a block weighing ![]() . The rotation of the spool is controlled by a friction brake that can be activated if it is subjected to a pushing force,
. The rotation of the spool is controlled by a friction brake that can be activated if it is subjected to a pushing force, ![]() as shown. If the coefficient of static friction at the contact surface of the spool and the brake is
as shown. If the coefficient of static friction at the contact surface of the spool and the brake is ![]() , determine the minimum magnitude of
, determine the minimum magnitude of ![]() needed to prevent the spool from rotation.
needed to prevent the spool from rotation.
ANSWER
![]()
