Forces and Moments: Couple moment
Moment of a couple
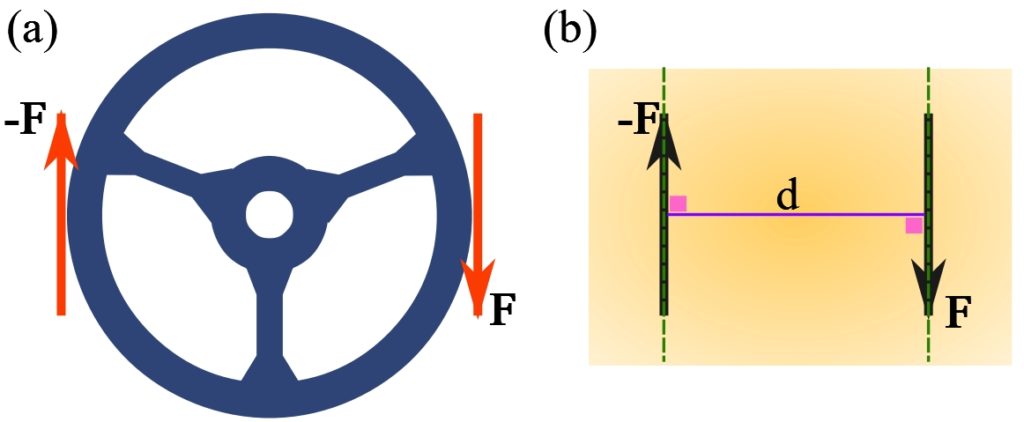
Imagine that you want to turn a valve, or the steering wheel of a car (Fig. 3.20a). You can do it by two hands as one hand pushes up and the other one pulls down the valve or the steering wheel. As a result, the valve or the steering wheel rotates. Your hands (ideally) generated two equal and parallel forces but with opposite directions. This pair of forces creates a turning effect,referred to as a couple formally defined as below.
A couple. A couple is defined as a pair of parallel but noncollinear forces that have the same magnitude but opposite directions (Fig. 3.20b). Each force is referred to as a couple force. Because the lines of action of the couple forces are parallel and noncollinear, they are in the same plane. The (perpendicular) distance, ![]() , between the lines of action of the parallel forces is called the perpendicular distance or moment arm between the forces.
, between the lines of action of the parallel forces is called the perpendicular distance or moment arm between the forces.
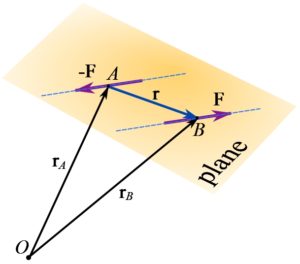
The moment created by a couple is called a couple moment. To find the couple moment of a couple, an arbitrary point, ![]() , in the space is considered and the moment of each couple force is calculated about that point (Fig. 3.21),
, in the space is considered and the moment of each couple force is calculated about that point (Fig. 3.21),
![]()
where ![]() and
and ![]() are position vectors directed from
are position vectors directed from ![]() to any points (A and B in this case) on the lines of action of the forces. Let
to any points (A and B in this case) on the lines of action of the forces. Let ![]() . Then,
. Then, ![]() is a position vector linking the two points on the lines of actions. According to the choices of
is a position vector linking the two points on the lines of actions. According to the choices of ![]() and
and ![]() ,
, ![]() is obviously independent of the choice of
is obviously independent of the choice of ![]() ; therefore, the couple moment becomes independent of
; therefore, the couple moment becomes independent of ![]() and also the position vectors
and also the position vectors ![]() and
and ![]() . Thereby, the couple moment is formulated as,
. Thereby, the couple moment is formulated as,
(3.20) ![]()
Equation 3.20 indicates that a couple moment of a particular couple only depends on the forces and their distance and does not depend on the point about which the couple moment is calculated. Therefore, a couple moment (vector) is not assigned to any point and can be freely positioned anywhere in the space. Such a vector is called a free vector.
Remark: note the difference between the terms the moment of a force about a point and the moment of a couple.
Remark: a force is a sliding vector meaning that it can slide along its line of action without affecting the calculations. A couple moment is a free vector meaning that it can be placed anywhere in the space or the body without affecting the calculations.
A couple moment can be determined using both scalar and vector formulations:
Scalar formulation. Since the forces of a couple are coplanar (Fig 3.22), the magnitude of couple moment can be determined by summing the moment of each force about an arbitrary point, ![]() , in the plane as demonstrated in Fig. 3.22,
, in the plane as demonstrated in Fig. 3.22,
(3.21) ![]()
where ![]() and
and ![]() are the moments arms (perpendicular distance) of the forces.
are the moments arms (perpendicular distance) of the forces.
Determined by the right-hand rule, the direction of the couple moment is perpendicular to the plane of the couple forces and the sense of rotation follows the fingers curled (Fig. 3.22).
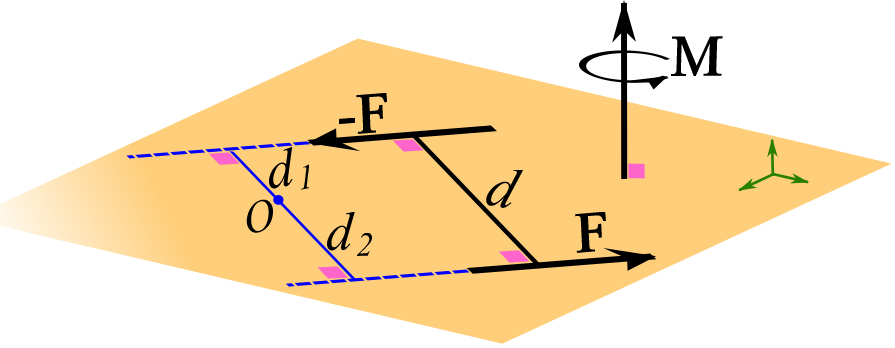
Calculation of Eq. 3.21 can be interpreted as the moment of one of the forces about a point on the line of action of the other force.
Vector formulation. The vector formulation is in fact Eq. 3.20. This formulation is used when a couple moment is needed to be written in its vector form. Like the scalar formulation, the vector formulation can be interpreted as calculating the moment of one of the couple forces about a point on the line of action of the other force.
Equivalent couples
Two couples are equivalent if they produce equal (couple) moments, i.e., moments with the same magnitude and direction,
(3.22) ![]()
where ![]() and
and ![]() are forces from different couples. The notation
are forces from different couples. The notation ![]() means equivalent.
means equivalent.
