Internal Forces: Relationships between Load, Shear, and Moments
Direct derivation of the functions ![]() and
and ![]() by the method of sections may be tedious. The direct application of the method of sections can be avoided by deriving the relationship between the load, shear, and bending moment. In this section, four relationships are derived:
by the method of sections may be tedious. The direct application of the method of sections can be avoided by deriving the relationship between the load, shear, and bending moment. In this section, four relationships are derived:
1- point force AND shear
2- distributed load AND shear
3- shear AND bending moment
4- couple moment AND bending moment
1- Point Force and Shear
Consider a downward point force acting at a point ![]() of a beam (Fig. 7.16a). To find the relationship between the shear and the point force, a segment of the beam as shown in Fig. 7.16a is considered. The segment contains the force (point of application) and has a fractional length of
of a beam (Fig. 7.16a). To find the relationship between the shear and the point force, a segment of the beam as shown in Fig. 7.16a is considered. The segment contains the force (point of application) and has a fractional length of ![]() .
.
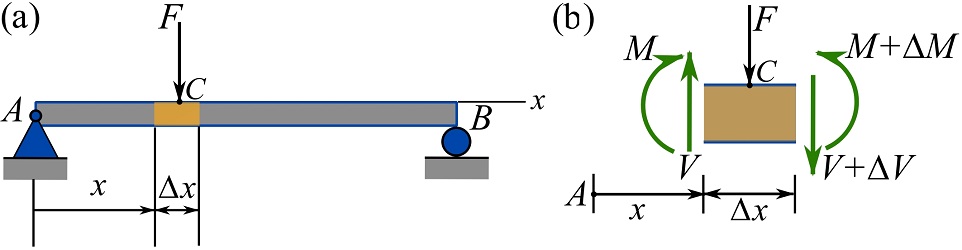
Isolating the segment exposes the internal forces on its FBD as shown in Fig. 7.16b. The beam is free of axial load. The values of the function ![]() and
and ![]() , evaluated at
, evaluated at ![]() , are denoted as
, are denoted as ![]() and
and ![]() respectively. At a distance
respectively. At a distance ![]() away from point
away from point ![]() , the shear force and the bending moment generally vary to
, the shear force and the bending moment generally vary to ![]() and
and ![]() . The force equilibrium for the free segment is,
. The force equilibrium for the free segment is,
![]()
which can be written as,
(7.1) ![]()
where ![]() and
and ![]() denote the shear right before and after point
denote the shear right before and after point ![]() respectively.
respectively.
Equation 7.1 states that a point force ![]() acting on a beam creates a jump, with a magnitude of
acting on a beam creates a jump, with a magnitude of ![]() , in the values of
, in the values of ![]() . The jump appears as a jump discontinuity in the diagram of
. The jump appears as a jump discontinuity in the diagram of ![]() .
.
Remark: exactly at the application point of a point force, the value of shear is undefined due to the jump discontinuity.
EXAMPLE 7.3.1
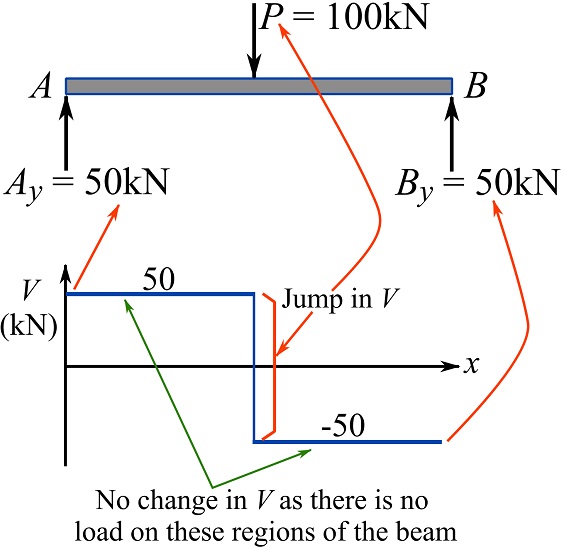
Plot the shear diagram of the beam shown. Use Eq. 7.1.

SOLUTION
Draw the FBD of the beam and solve for the support reactions.
The FBD with solved support reactions are demonstrated in the figure below.
Start from the known shear at point ![]() and use
and use ![]() to determine the shear along the beam axis. Observe the jump in the values of
to determine the shear along the beam axis. Observe the jump in the values of ![]() at the point where the external load
at the point where the external load ![]() acts; the jump in values is
acts; the jump in values is ![]() .
.
2- Distributed load and Shear
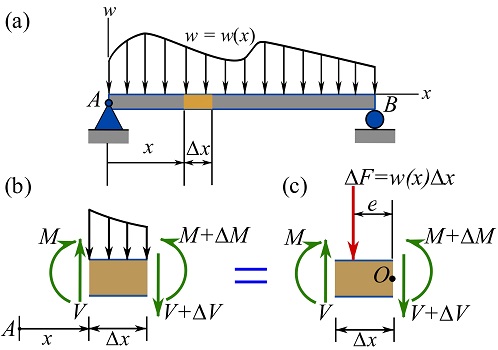
Consider a beam under a continuous distributed load expressed by a function ![]() . As shown in Fig. 7.17a, positive values of
. As shown in Fig. 7.17a, positive values of ![]() are associated with downward force on the beam.
are associated with downward force on the beam.
To obtain the relationship between ![]() and
and ![]() , a beam segment with a fractional length
, a beam segment with a fractional length ![]() is considered at an arbitrary distance
is considered at an arbitrary distance ![]() from the left-hand side of the beam (Fig. 7.17a). The FBD of the segment is constructed as shown in Fig 7.17b. The beam is free of axial load. The shear force
from the left-hand side of the beam (Fig. 7.17a). The FBD of the segment is constructed as shown in Fig 7.17b. The beam is free of axial load. The shear force ![]() and the bending moment
and the bending moment ![]() at
at ![]() are denoted as
are denoted as ![]() and
and ![]() respectively. The shear force and bending moment at a distance
respectively. The shear force and bending moment at a distance ![]() are denoted as
are denoted as ![]() and
and ![]() respectively.
respectively.
As shown in Fig 7.17c, the part of the distributed load, ![]() , acting on the segment is replaced with its (equivalent) resultant force with the magnitude of
, acting on the segment is replaced with its (equivalent) resultant force with the magnitude of ![]() . The location at which
. The location at which ![]() acts on the segment is shown by
acts on the segment is shown by ![]() in the figure. In fact,
in the figure. In fact, ![]() acts somewhere along the length of the segment; in other words,
acts somewhere along the length of the segment; in other words, ![]() where
where ![]() . It will be seen that the location of
. It will be seen that the location of ![]() does not affect the calculations. Writing the force equation of equilibrium for the FBD of the segment leads to the following relationship.
does not affect the calculations. Writing the force equation of equilibrium for the FBD of the segment leads to the following relationship.
![]()
Therefore, letting ![]() and taking the limit of both sides as,
and taking the limit of both sides as,
![]()
leads to,
(7.2) ![]()
This equation indicates that at any point ![]() along the axis of the beam, the slope of the diagram of
along the axis of the beam, the slope of the diagram of ![]() equals the negative value of
equals the negative value of ![]() . This is the geometrical interpretation of Eq. 7.2.
. This is the geometrical interpretation of Eq. 7.2.
An alternative form of the relationship between ![]() and
and ![]() is obtained by writing Eq. 7.2 as
is obtained by writing Eq. 7.2 as ![]() and integrating both sides,
and integrating both sides,
![]()
leads to,
(7.3) ![]()
where ![]() and
and ![]() such that
such that ![]() are the coordinates of two points
are the coordinates of two points ![]() and
and ![]() on the axis of the beam.
on the axis of the beam.
The geometrical interpretation of Eq. 7.3 indicates that the variation of the shear between two points on the beam equals the area (negative value) under the distributed load between the two points.
Equation 7.3 can be utilized to find ![]() . If the shear,
. If the shear, ![]() is known at a starting point,
is known at a starting point, ![]() , then the shear
, then the shear ![]() at any arbitrary point with the coordinate
at any arbitrary point with the coordinate ![]() is,
is,
(7.4) ![]()
Note that the integration variable is a dummy variable and therefore renamed to ![]() .
.
EXAMPLE 7.3.2
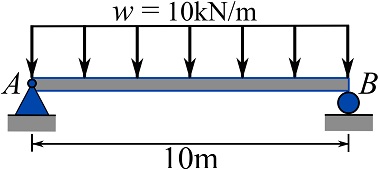
For the loaded beam shown.
1- Plot the shear diagram of the beam. Use Eq. 7.4.
2- Using the geometrical interpretation of the relationship between external load and shear force, show that ![]() and
and ![]() at
at ![]() and
and ![]() respectively.
respectively.
SOLUTION
Part 1
Draw the FBD of the beam and solve for the support reactions.
The FBD with solved support reactions are demonstrated in the figure below.
Starting from point ![]() , determine the shear at any point
, determine the shear at any point ![]() using Eq. 7.4 as,
using Eq. 7.4 as,
![]()
Observe the relationship between ![]() and the slope of
and the slope of ![]() ; the slope,
; the slope, ![]() is constant as
is constant as ![]() is constant.
is constant.
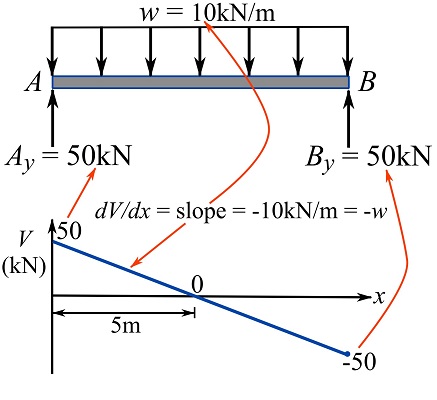
Part 2
Use the relationship ![]()

3– Shear and Bending Moment.
Shear and moment relationship can be obtained by writing the moment equation of equilibrium about point ![]() of the free segment shown in Fig. 7.17c as,
of the free segment shown in Fig. 7.17c as,
![Rendered by QuickLaTeX.com \[\begin{split}\circlearrowleft{+} \sum M_O=0 &\implies -M-(V)(\Delta x) + (\Delta F)(e)+(M+\Delta M)=0\\&\implies -(V)(\Delta x)+(w(x)\Delta x)(k\Delta x)+\Delta M=0\\&\implies -(V)(\Delta x)+(kw(x))(\Delta x)^2+\Delta M=0\\&\implies V=(kw(x))(\Delta x)+\frac{\Delta M}{\Delta x}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f11714867c0590147f09e1025ef873dc_l3.png)
and letting ![]() ,
,
(7.5) ![]()
This relationship indicates that at any point ![]() along the axis of the beam, the slope of the diagram of
along the axis of the beam, the slope of the diagram of ![]() equals the value of
equals the value of ![]() .
.
The integral form of Eq. 7.5 is achieved by writing ![]() and integrating both sides as,
and integrating both sides as,
(7.6) ![]()
Equation 7.6 indicates that the variation of the bending moment between two points on the beam equals the area under the shear diagram between the two points.
Using Eq. 7.6, the function ![]() can be determined. If the bending moment,
can be determined. If the bending moment, ![]() is known at a starting point,
is known at a starting point, ![]() , then the bending moment
, then the bending moment ![]() at any arbitrary point with the coordinate
at any arbitrary point with the coordinate ![]() is,
is,
(7.7) ![]()
EXAMPLE 7.3.3
For the loaded beam shown.
1- Plot the moment diagram of the beam. Use Eq. 7.7.
2- Using the geometrical interpretation of the relationship between shear and bending moment, show that ![]() at
at ![]() .
.

SOLUTION
Part 1
Drawing the FBD, obtaining the support reactions, and drawing the shear diagram are already done and demonstrated in Example 7.3.1.
To determine ![]() , use Eq. 7.7 for
, use Eq. 7.7 for ![]() and
and ![]() .
.
For ![]() ,
,
![Rendered by QuickLaTeX.com \[\begin{split}M(x)&=M_A + \int_0^x V(t)dt=0+\int_0^x 50dt\\&\therefore M(x)=50x\text{ kN.m}\quad 0\le x\le 5\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-adc3b0f6f10265e86a27bab2ee07586c_l3.png)
For ![]() ,
,
![Rendered by QuickLaTeX.com \[\begin{split}M(x)&=M_A + \int_0^x V(t)dt=0+\int_0^5 50dt+\int_5^x -50dt\\&\therefore M(x)=500 -50x \text{ kN.m}\quad 5\le x\le 10\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e1b4769409e0ec297e3c00486be3d6ec_l3.png)
Therefore,
![]()
The diagram of ![]() is as follows,
is as follows,
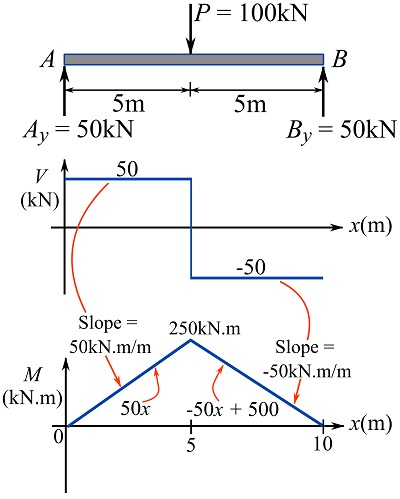
Part 2
Use the relationship ![]() .
.
![]()
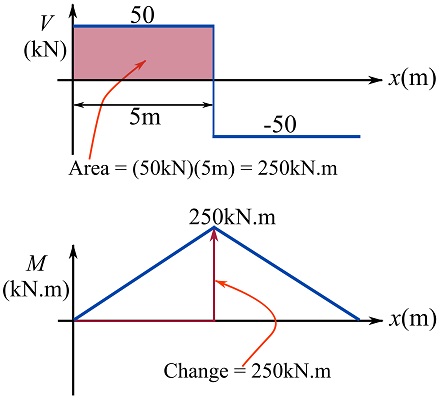
EXAMPLE 7.3.4
For the loaded beam shown.
1- Plot the moment diagram of the beam. Use Eq. 7.7.
2- Using the geometrical interpretation of the relationship between shear and bending moment, show that ![]() at
at ![]() .
.
3- Show that the change ![]() equals the area under
equals the area under ![]() diagram.
diagram.

SOLUTION
Part 1
Drawing the FBD, obtaining the support reactions, and drawing the shear diagram are already done and demonstrated in Example 7.3.2.
To determine ![]() , use Eq. 7.7 for
, use Eq. 7.7 for ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{split}M(x)&=M_A + \int_0^x V(t)dt=0+\int_0^x -10x+50dt\\&\therefore M(x)=-5x^2+50x\text{ kN.m}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f4d1ef62c8f7e9aec27eb8a223bba335_l3.png)
The diagram of ![]() is as follows,
is as follows,
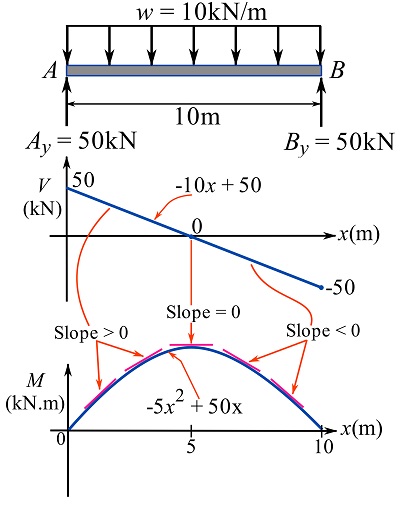
Part 2
Use the relationship ![]() .
.
![]()
See figure below for the demonstration.

Part 3
![]()
See the above figure for the demonstration.
4- Couple Moment and Bending Moment
Consider an external couple moment acting at a point ![]() of a beam (Fig. 7.18a). To find the relationship between the bending moment and the couple moment, a segment of the beam as shown in Fig. 7.18a is considered.
of a beam (Fig. 7.18a). To find the relationship between the bending moment and the couple moment, a segment of the beam as shown in Fig. 7.18a is considered.

The FBD of the segment is shown in Fig 7.18b. Writing the moment equation of equilibrium for the free segments lead to,
![]()
Letting ![]() , results in,
, results in,
(7.8) ![]()
where ![]() and
and ![]() denote the bending moment right before and after point
denote the bending moment right before and after point ![]() respectively.
respectively.
Equation 7.9 states that a couple moment ![]() acting on a beam creates a jump, with a magnitude of
acting on a beam creates a jump, with a magnitude of ![]() , in the values of
, in the values of ![]() . The jump appears as a jump discontinuity in the diagram of
. The jump appears as a jump discontinuity in the diagram of ![]() .
.
Remark: the value of bending moment exactly at the application point of a couple moment is undefined due to the jump discontinuity.
Use the following interactive tool to obtain SFD and BMD of different beams (simply supported and cantilever beams) with different supports and loads. Observe the variations within each diagram upon changing the loads and other inputs.
Note that the numerical results may contain negligible error due to round off. Also, In some cases you may observe that the support reaction of the roller becomes a pulling force on the beam. In this case, assume that the support is a roller in a frictionless slot
