Forces and Moments: Forces
Definition of force
In general, force is perceived as push or pull. Forces arise from different sources/causes like gravity, contact forces between bodies, pressure force by fluids on surface of solids, friction forces, electrostatic forces on charged particles, etc.
Physically, force has a magnitude and a direction in the space, and therefore, it is a vector quantity called the force vector. In this regard, the terms force and force vector are equivalent. Calculations regarding forces follow the concepts and methods presented in Chapter 2.
The SI unit of force is Newton (N). A force vector has the dimension ![]() , being equal to
, being equal to ![]() in the SI unit system (see Section 1.2). The direction of a force vector can be expressed using a unit vector. This unit vector shows the direction in the (geometrical) space. We can also have a graphical representation of a force vector. This graphical representation is by the means of an arrow as discussed in Section 2.2. The length of an arrow representing a force vector can be proportional to the vector’s magnitude following some scale.
in the SI unit system (see Section 1.2). The direction of a force vector can be expressed using a unit vector. This unit vector shows the direction in the (geometrical) space. We can also have a graphical representation of a force vector. This graphical representation is by the means of an arrow as discussed in Section 2.2. The length of an arrow representing a force vector can be proportional to the vector’s magnitude following some scale.
Denoting a force vector as ![]() , we can write,
, we can write,
(3.1) ![]()
where ![]() is the magnitude of the force and
is the magnitude of the force and ![]() is the unit vector expressing the direction of
is the unit vector expressing the direction of ![]() . Note that
. Note that ![]() has the unit of Newton, and the unit vector has no dimension and unit. Equation 3.1 readily implies that,
has the unit of Newton, and the unit vector has no dimension and unit. Equation 3.1 readily implies that,
(3.2) ![]()
Line of action of a force. The line of action of a force or a force vector ![]() is a line that is collinear with the force vector (arrow representing the force).
is a line that is collinear with the force vector (arrow representing the force).
Like any vector, a force vector ![]() can be resolved into its Cartesian components using the CVN,
can be resolved into its Cartesian components using the CVN,
(3.3) ![]()
where ![]() are the scalar components.
are the scalar components.
A graphical representation of ![]() in the Cartesian frame is shown in Fig. 3.1.
in the Cartesian frame is shown in Fig. 3.1.
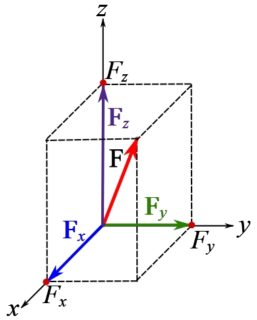
We say a body is subjected to a force (or a system of forces), or a force acts on a body. This expresses the fact that a force is acting or exerted at a particular location of the body. Therefore, the location at which a force vector is acting is deterministically important and not arbitrary. This is graphically demonstrated by drawing the force vector with its tail or head touching the point at which the force acts (Fig. 3.2a). Depending on the tail or the head of the vector touching the point, this representation may also imply a sense of pull or push by the force (Fig 3.2a).
Parallel forces. Two or more forces are called parallel if their line of actions are parallel. For example, ![]() ,
, ![]() , and
, and ![]() are parallel in Fig. 3.2b.
are parallel in Fig. 3.2b.
Collinear forces. Two or more forces are called collinear if they share the same line of action. Consequently, collinear forces are parallel. However, parallel forces may not be collinear. For example, ![]() ,
, ![]() , and
, and ![]() are collinear in Fig. 3.2b.
are collinear in Fig. 3.2b.
Concurrent forces. Two or more forces are called concurrent if their lines of action intersect at a common point. For example, ![]() ,
, ![]() , and
, and ![]() are concurrent in Fig. 3.2b.
are concurrent in Fig. 3.2b.
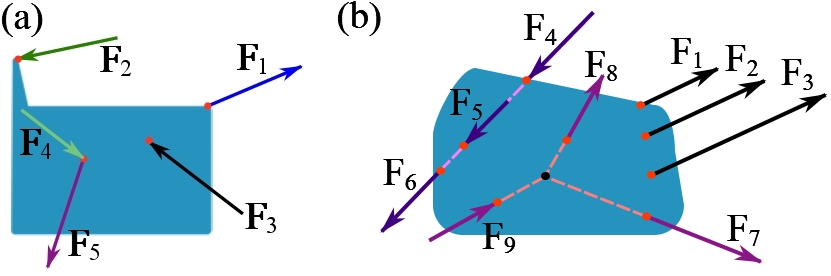
a force always accompanies a point at which the force is acting.
Concentrated force. In reality, forces are continuously distributed over areas. For example, we perceive and feel that the ground reaction force due to our weight is distributed on the soles of our feet; we do not feel a sharp feeling of a force there. In fact, all forces in nature are distributed, and there is no force concentrated at (or acting on) a point. However, we idealize or approximate a distributed force by a concentrated force. This idealization is performed when the area on which the load is distributed is relatively small compared to the size of the body.
Resultant force
Let ![]() be a system of
be a system of ![]() forces (set of forces), their resultant or the resultant force
forces (set of forces), their resultant or the resultant force ![]() is a vector sum over the forces (see Section 2.4),
is a vector sum over the forces (see Section 2.4),
(3.4) ![]()
Remark: vector addition of forces does not depend on the location of forces on a body.
The calculation procedure of resultants of forces can be presented separately for coplanar and spatial force systems.
Coplanar force systems (Two-dimensions)
A coplanar force system or a system of coplanar forces is a set of forces with their lines of action all in the same plane. Therefore, each force in a coplanar force system has two Cartesian components in a plane Cartesian coordinate system as presented in Section 2.4.2. With ![]() and
and ![]() being the axes of a Cartesian frame, a planar
being the axes of a Cartesian frame, a planar ![]() is written in CVN as,
is written in CVN as,
(3.5a) ![]()
The the following equations hold for the magnitude, and scalar components of planar forces,
(3.5b) ![]()
where ![]() is the angle of
is the angle of ![]() with the
with the ![]() axis as shown in Fig. 3.3.
axis as shown in Fig. 3.3.
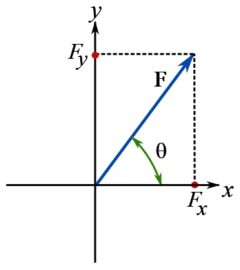
Note that a new notation for the magnitude of ![]() (not its components) is defined as
(not its components) is defined as ![]() being a non-bold capital letter. We will used
being a non-bold capital letter. We will used ![]() instead of
instead of ![]() when denoting the magnitude of a planar force. This labeling approach applies to the two-dimensional calculation of any vectors for simplicity.
when denoting the magnitude of a planar force. This labeling approach applies to the two-dimensional calculation of any vectors for simplicity.
To determine the resultant force of a coplanar force system, the equations presented in Sections 2.4.2 and 2.4.3 are implemented. Here, we repeat the equations for a force system.
For a system of coplanar forces ![]() , if each force is expressed in CVN as,
, if each force is expressed in CVN as,
![Rendered by QuickLaTeX.com \[\begin{split} \bold F_1&=F_{1x}\bold i + F_{1y}\bold j\\ \bold F_2&=F_{2x}\bold i + F_{2y}\bold j\\ &\vdots\\ \bold F_n&=F_{nx}\bold i + F_{ny}\bold j \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-470598cce4a165eeb676af59cd7a7fee_l3.png)
the resultant force ![]() is determined as,
is determined as,
(3.6a) ![]()
which is written in the following concise way,
(3.6b) ![]()
EXAMPLE 3.1.1
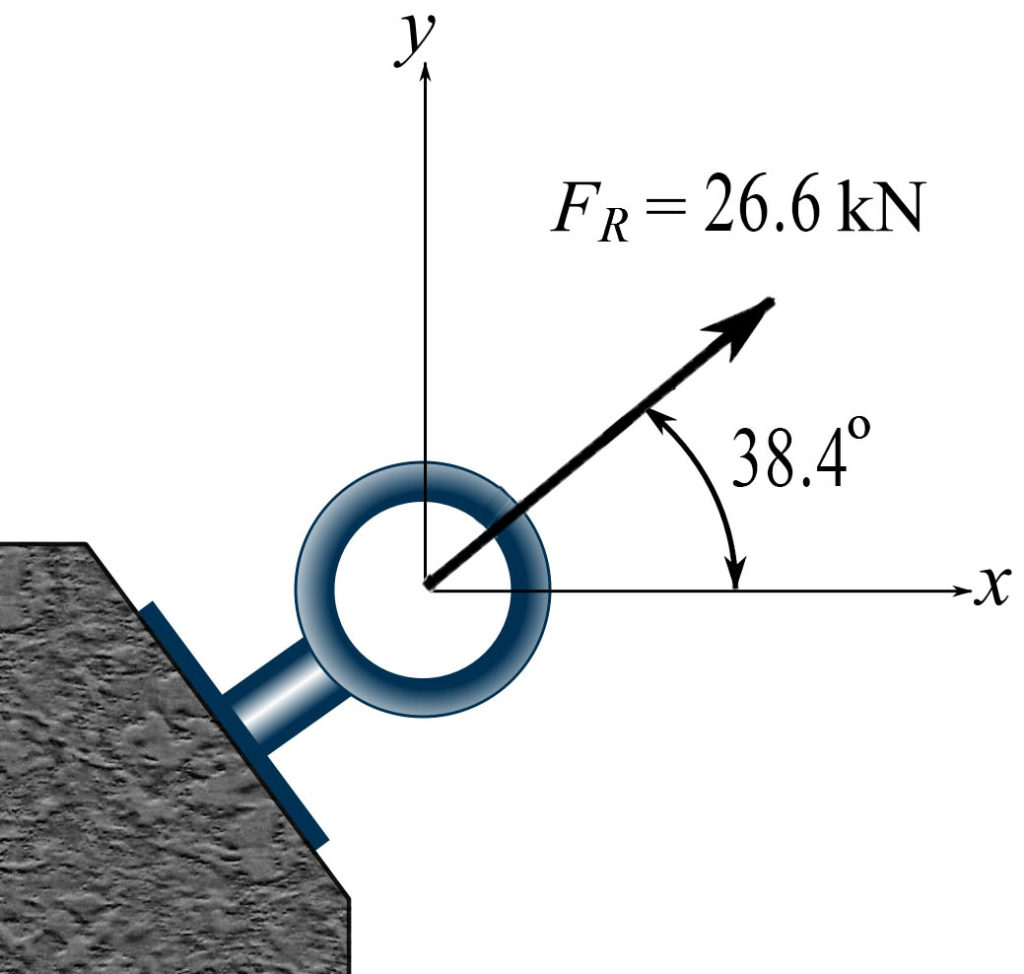
Determine the resultant force of the cable forces shown in the figure. Obtain the force vector, its magnitude, and its direction measured from the positive x-axis shown.
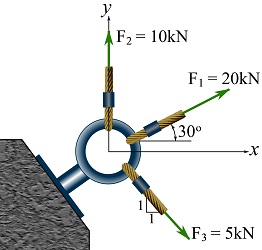
SOLUTION
![Rendered by QuickLaTeX.com \[\begin{split}\bold F_1&=\{20\cos 30^\circ \bold i+20\sin 30^\circ\bold j\}=\{17.3\bold i+10.0\bold j\}\text{ kN}\\\bold F_2&=\{0\bold i + 10\bold j\}\text{ kN}\\\bold F_3&=\{5\cos 45^\circ\bold i+5\sin 45^\circ\bold j\}=\{3.5\bold i - 3.5\bold j\}\text{ kN}\\\therefore \bold F_R&=\bold F_1 + \bold F_2 + \bold F_3= \{17.3+0+3.5\}\bold i+\{10.0+10.0-3.5\}\bold j\\&=\{20.8\bold i+16.5\bold j\}\text{ kN}\\\implies F_R&=|\bold F_R|=\sqrt{20.8^2+16.5^2}=26.6 \text{ kN}\\\\ \theta&=\arctan\frac{16.5}{20.8}=38.4^\circ\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-df47e7660537985d3fe705b30d5487ee_l3.png)
Spatial force systems (three-dimensions)
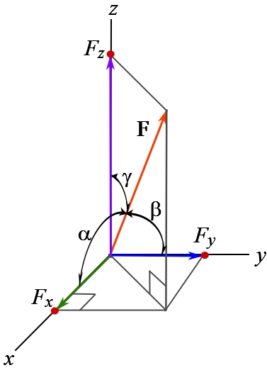
A spatial system of forces, is a general force system with forces not necessarily lying in one plane. A spatial force ![]() can be represented by three Cartesian components as formulated in Section 2.4.4. With x, y and z being the axes of a Cartesian frame,
can be represented by three Cartesian components as formulated in Section 2.4.4. With x, y and z being the axes of a Cartesian frame, ![]() is written in CVN as,
is written in CVN as,
(3.7a) ![]()
The following equations hold for the magnitude, and scalar components of the force,
(3.7b) ![Rendered by QuickLaTeX.com \[\begin{split}|\bold F|&=\sqrt{F_x^2 +F_y^2 +F_z^2}\\\cos \alpha=\frac{F_x}{|\bold F|} \quad &\cos \beta=\frac{F_y}{|\bold F|} \quad \cos \gamma=\frac{F_z}{|\bold F|} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7aaebd424753a6b2420bbdb2b5fb6779_l3.png)
where ![]() are the coordinate direction angles as shown in Fig. 3.4.
are the coordinate direction angles as shown in Fig. 3.4.
The resultant force ![]() of a system of spatial forces containing
of a system of spatial forces containing ![]() expressed in CVN is,
expressed in CVN is,
(3.8) ![]()
EXAMPLE 3.1.2
A box beam is subjected to the forces as shown. Express each force in CVN and determine the magnitude and coordinate direction angles of the resultant force.

SOLUTION
To express the ![]() , the scalar components of
, the scalar components of ![]() are determined and we write
are determined and we write ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{split}F_{1x} &= 0 \rm{N}\\F_{1y} &= 500 \frac{3}{5} = 300 \rm{N}\\F_{1z} &= -500 \frac{4}{5} = -400 \rm{N}\\\implies \bold F_1&=\{0\bold i + 300\bold j - 400\bold k\}\rm N\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bbfd62379924a36425ae7e5523ec66a5_l3.png)
And for ![]() ,
,
![Rendered by QuickLaTeX.com \[\begin{split}F_{2x} &= 150\cos(60^\circ)= 75\rm{N}\\F_{2y} &= 150\cos(150^\circ)= -130\rm{N}\\F_{2z} &= 150\cos(60^\circ)= 75\rm{N}\\\implies \bold F_2&=\{75\bold i -130\bold j +75\bold k\}\rm N\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e605f4a95514e2b3ee2ae499bcdd6dbc_l3.png)
Therefore,
![]()
Leading to,
![]()
The direction angles of ![]() are,
are,
![Rendered by QuickLaTeX.com \[\begin{split}\cos \alpha &= \frac{75}{374.4} \Rightarrow \alpha = 78.5^\circ \\\cos \beta &= \frac{170}{374.4} \Rightarrow \beta = 63.0^\circ \\\cos \gamma &= \frac{-325}{374.4} \Rightarrow \gamma = 150.1^\circ\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-10ce2b6de04a254ac11d23f0ce160695_l3.png)
Force directed along a line
In many problems, a force is directed along a line-shape physical object or structure like a cable or a bar. In such a case, the line of action of the force is collinear with the direction of the object (Fig. 3.5). The line of action of the force is, therefore, determined by two points along the structure.
To determine a force directed along a line, we initially choose (or consider a given) a Cartesian coordinate system. Choosing a point as the coordinate system origin (if not given) is arbitrary, however, we should try to wisely choose a point that will simplify the calculations. Then, two points, say A and B, on the line of action or the object are identified. These are points with known coordinates or points that their coordinates are easy enough to calculate (Fig. 3.5). Considering the position vectors of A and B, we find the vector ![]() as,
as,
(3.9) ![]()
The unit vector ![]() is obtained by normalizing
is obtained by normalizing ![]() by its magnitude (length),
by its magnitude (length), ![]() , assuming AB is the direction of the force. Consequently, the force vector
, assuming AB is the direction of the force. Consequently, the force vector ![]() can be written as,
can be written as,
(3.10) ![]()
As shown in Fig. 3.5, the graphical representation of ![]() ,
, ![]() and
and ![]() are collinear. Note that
are collinear. Note that ![]() has the dimension of force,
has the dimension of force, ![]() has the dimension of length, and the unit vector
has the dimension of length, and the unit vector ![]() has no dimension. Despite having different dimensions and units, all the vector quantities can be graphically shown in one Cartesian coordinate system (frame).
has no dimension. Despite having different dimensions and units, all the vector quantities can be graphically shown in one Cartesian coordinate system (frame).
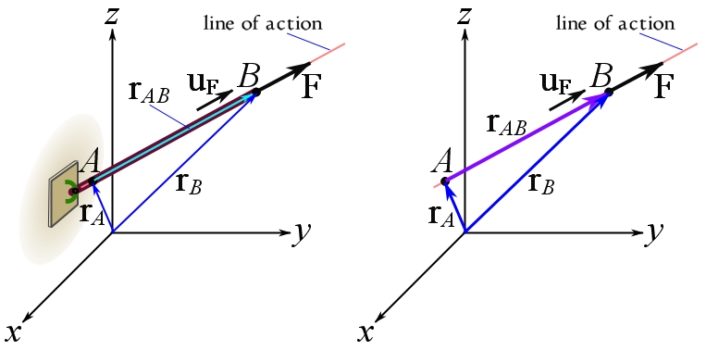
The following interactive tool illustrates obtaining a force vector directed along a line with two known points.
EXAMPLE 3.1.3
Determine the magnitude and coordinate direction angles of the resultant force. ![]() ,
, ![]() and
and ![]() .
.
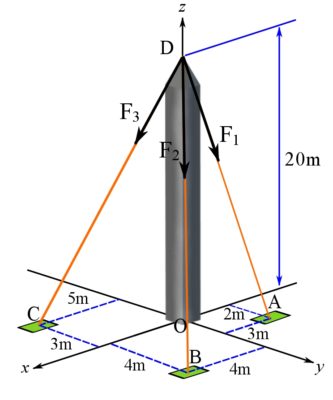
SOLUTION
The following position vectors are needed to determine the directions of the forces.
![Rendered by QuickLaTeX.com \[\begin{split}\bold u_{DA} &= \frac{\bold r_A - \bold r_D}{| \bold r_{DA} |} = \frac{-3 \bold i + 2 \bold j - 20 \bold k}{\sqrt{3^2 + 2^2 + 20^2}}\\\bold u_{DB} &= \frac{\bold r_B - \bold r_D}{| \bold r_{DB} |} = \frac{4\bold i + 4 \bold j - 20 \bold k}{\sqrt{4^2 + 4^2 + 20^2}}\\\bold u_{DC} &= \frac{\bold r_C - \bold r_D}{| \bold r_{DC} |} = \frac{5 \bold i - 3 \bold j - 20\bold k}{\sqrt{5^2 + 3^2 + 20^2}}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a185cab6860f5eabbbdbc6beed5de39f_l3.png)
The forces are found as,
![Rendered by QuickLaTeX.com \[\begin{split}\bold F_1 &= |\bold F_1|\bold u_{DA} = 400 \frac{-3 \bold i + 2 \bold j - 20 \bold k}{\sqrt{3^2 + 2^2 + 20^2}} \\&=\{-59.04 \bold i + 39.37 \bold j - 393.65 \bold k\}\rm N\\\bold F_2 &= |\bold F_2|\bold u_{DB} = 200 \frac{4\bold i + 4 \bold j - 20 \bold k}{\sqrt{4^2 + 4^2 + 20^2}} \\&=\{38.49 \bold i + 38.49 \bold j - 192.45 \bold k\} \rm N\\\bold F_3 &= |\bold F_3|\bold u_{DC}= 300 \frac{5 \bold i - 3 \bold j - 20\bold k}{\sqrt{5^2 + 3^2 + 20^2}}\\&=\{72 \bold i - 43.20 \bold j - 288 \bold k\} \rm N\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0553c70d40142860f71e4c6760169558_l3.png)
Therefore, the resultant force ![]() is,
is,
![Rendered by QuickLaTeX.com \[\begin{split}\bold F_R &= \bold F_1 + \bold F_2 + \bold F_3\\&=(-59.04 + 38.49 + 72 )\bold i + (39.37 + 38.49 - 43.2)\bold j + (-393.65 - 192.45 - 288) \bold k \\&=\{51.45 \bold i +34.66 \bold j - 874.10 \bold k\} \rm N\\|\bold F_R| &= 876.72 \rm N\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4aa94e1c23a69e8a88607d00a02113df_l3.png)
The coordinate direction angles ![]() ,
, ![]() , and
, and ![]() (the angls of the resultant force with
(the angls of the resultant force with ![]() ,
, ![]() , and
, and ![]() axes respectively) are, therefore, determined as,
axes respectively) are, therefore, determined as,
![Rendered by QuickLaTeX.com \[\begin{split}\alpha &= \arccos (\frac{51.45}{876.72}) = 86.64^{\circ} \\\beta &= \arccos (\frac{34.66}{876.72}) = 87.70^{\circ} \\\gamma &= \arccos (\frac{-874.10}{876.72}) = 175.94^{\circ}\end {split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7d3a3734315785ebc54e15c38bbe1998_l3.png)
Context: Force directed along a Line
- There is a relationship between position vectors (e.g. member length and angles) and force vectors (e.g. force carried by a member).
- In two dimensional systems, simple trigonometric rules can relate vector components and the angle between vectors. This approach is much more complicated in 3-D systems, so another approach is used instead: dot products.
- Force directed along a line is most easily visualized in cables but occurs in many other members (such as columns, struts, and truss members).
- Engineers select member start and end points based on many factors (e.g. aesthetics, materials, ease of construction) but the most important factor is optimizing how force is carried through the member. For instance, in a system supported by many cables, engineers may proportion cable start and end points to ensure that each cable carries approximately the same forces under the expected loads.
Applications: Why is force along a line important?
The Port Mann Bridge between Surrey and Coquitlam (Vancouver area) opened in 2012 and has one of the longest spans of a cable stayed bridge in North America (470 m) (Fig. 3.6a). To support the roadway, dozens of steel cables connect to one of two large reinforced concrete towers.
Engineers need to consider how much force is carried in each cable to ensure that the tower is not excessively loaded on one side (which would cause the tower to bend or twist). Since each cable acts at a different angle, engineers used force along a line concepts to determine the force in each cable and evaluate if the tower is loaded evenly and ensure that no cables are overloaded (i.e. at risk of snapping). For added complexity, engineers also need to account for how the cables deform (i.e. stretch) when they are under load to ensure they share loads as designed. Deformations are discussed in future courses.
Note that cable stayed bridges are commonly mistaken as suspension bridges. In cable stayed bridges, cables are connected directly between the roadway and the supporting towers (Fig. 3.6b) while suspension bridges (e.g. Golden Gate Bridge) have relatively small vertical cables (‘suspenders’) that transfer loads (weight of road and the traffic) into large curved cables that rest on top of towers and are anchored (held) to the ground (usually via giant concrete anchorage blocks) at either end of the bridge.

Force component using dot product
The component of a force along an arbitrary axis can be determined using the dot product. Let ![]() be a force and l an axis with its positive direction defined by a unit vector
be a force and l an axis with its positive direction defined by a unit vector ![]() as shown in Fig. 3.7. Then, the component of
as shown in Fig. 3.7. Then, the component of ![]() along l is denoted by
along l is denoted by ![]() and determined by the orthogonal projection of
and determined by the orthogonal projection of ![]() onto l. Using the dot product to formulate the orthogonal projection (see Chapter 2),
onto l. Using the dot product to formulate the orthogonal projection (see Chapter 2), ![]() is calculated as,
is calculated as,
(3.11) ![]()

Note that ![]() is the scalar component of
is the scalar component of ![]() along the l axis. Therefore, we can write,
along the l axis. Therefore, we can write,
![]()
EXAMPLE 3.1.4
Consider the flagpole shown in the figure. The pole is 15 meters high and stabilized by a cable/rope as shown. Due to the wind, a tension force ![]() with a magnitude of
with a magnitude of ![]() develops in the cable. Determine the force developed along the pole.
develops in the cable. Determine the force developed along the pole.
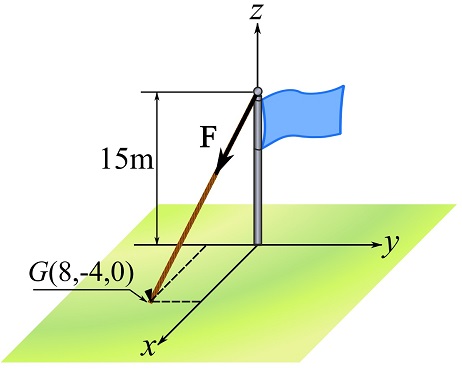
SOLUTION
1- determine the position vector ![]() .
.
![]()
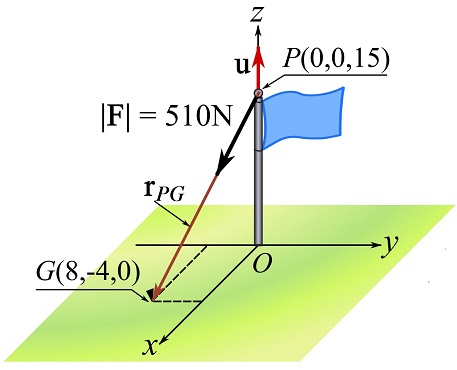
2- Find ![]() in CVN.
in CVN.
![Rendered by QuickLaTeX.com \[\begin{split}|\bold r_{PG}|&= \sqrt {8^2 + 4^2 +15^2} = 17.46 \text{ m}\\\bold F &= |\bold F|\frac{\bold r_{PG}}{|\bold r_{PG}|}=510 \frac{8\bold i - 4\bold j -15\bold k}{17.46}\text{N}\\\implies \bold F &=\{234\bold i -117\bold j -438\bold k\}\text {N}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b908c2d0bbfa57d912a972d9382c6cda_l3.png)
3- Project ![]() onto the z axis.
onto the z axis.
i) Find the unit vector on z axis.
![]()
ii)
![]()
where ![]() indicates that
indicates that ![]() in in the opposite direction of
in in the opposite direction of ![]() .
.
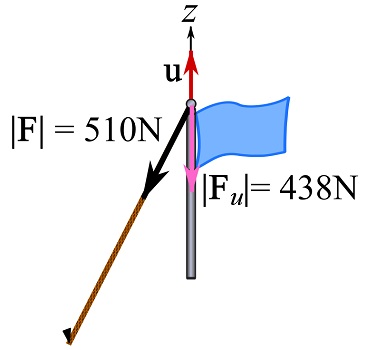
As in this example ![]() coincidentally, we can write
coincidentally, we can write ![]() .
.
