Friction: Equilibrium involving friction
If frictional forces act on a rigid body in equilibrium, the governing equations of friction should also be satisfied in addition to the equations of equilibrium. A stationary rigid body in equilibrium does not apparently slide against its surroundings. Therefore, the frictional forces acting on the body should either follow the non-slide, i.e. ![]() , or impending slide, i.e.
, or impending slide, i.e. ![]() , condition.
, condition.
EXAMPLE 8.2.1
A person intends to push on a stationary chest of drawers on the floor as shown. If the weight of the unit is 300N and the coefficient of static friction is ![]() , determine the magnitude of the pushing force that will cause the impending slide of the unit.
, determine the magnitude of the pushing force that will cause the impending slide of the unit.
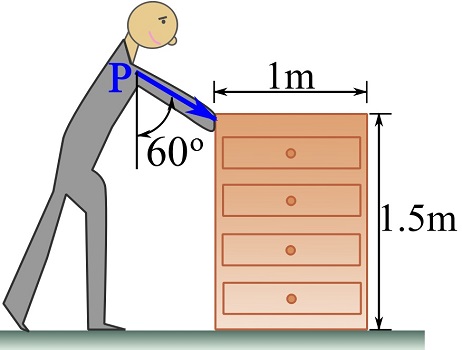
SOLUTION
Draw the FBD of the chest of drawers.
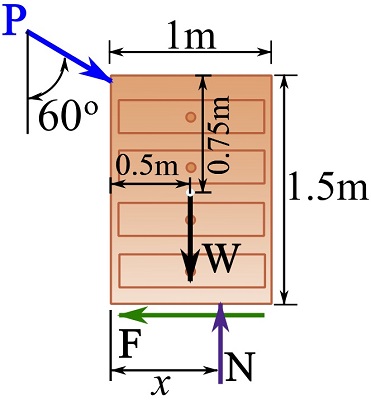
Note that the weight is applied at the geometric center (centroid) of the unit.
We need to check two cases: 1- impending slide, 2- tipping. The unit may tip before sliding, therefore, no sliding occurs at all. Note that only one of the two cases will happen.
1- Impending slide.
Assume that the unit is about to slide.
Therefore,
(1) ![]()
Based on the FBD, we can write the equilibrium equations as,
![Rendered by QuickLaTeX.com \[\begin{split}+\rightarrow \sum F_x&=0\implies P\sin 60^\circ - F=0\\+\uparrow \sum F_y&=0\implies -P\cos 60^\circ -300 + N =0\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9ea83755b20b6a03312def51f20e0fbd_l3.png)
Using Eq 1, the above equations become,
![Rendered by QuickLaTeX.com \[\begin{split}+\rightarrow \sum F_x&=0 \implies 0.866P-F=0\\+\uparrow \sum F_y&=0 \implies -0.5P-300+3.33F=0\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-96eaa7a4216766b7abd99ec6ce2a7463_l3.png)
forming a system of equations that leads to,
![]()
2- Tipping
The unit may tip about its bottom right corner; meaning that it rotates about the corner. At the onset of tipping, the corner of the unit is the only surface in contact with the floor, therefore, ![]() acts at the corner, i.e.
acts at the corner, i.e. ![]() . The FBD of the unit at the onset of tipping is then,
. The FBD of the unit at the onset of tipping is then,
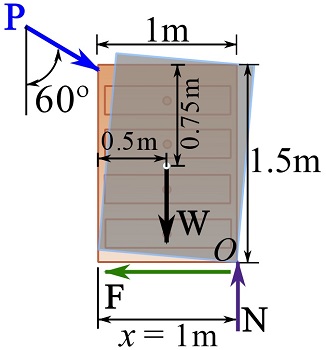
At the onset of tipping, the moment equilibrium must be satisfied, therefore,
![Rendered by QuickLaTeX.com \[\begin{split}\circlearrowleft\sum M_O&=0\implies -(P\sin 60^\circ)(1.5)+(P\cos 60^\circ)(1)+(W)(0.5)=0\\&\implies 0.8P=150\implies P=187.7\\&\therefore P_{\text{tipping}}=187.7\text{N}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1d1683c87e23ee7b2f33e49daae04c27_l3.png)
Because ![]() , the unit will slide rather than tipping.
, the unit will slide rather than tipping.
The magnitude of the pushing force that causes the unit to slide is ![]() .
.
EXAMPLE 8.2.2
A chest of drawers is at rest on a ramp with an inclination angle of ![]() . The coefficient of static friction between the unit and the ramp is
. The coefficient of static friction between the unit and the ramp is ![]() . Determine whether the sliding or tipping happens first when increasing the inclination angle slowly.
. Determine whether the sliding or tipping happens first when increasing the inclination angle slowly.
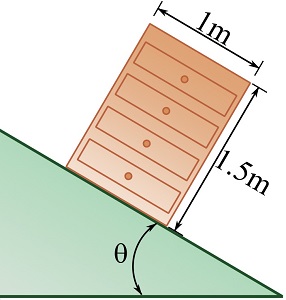
SOLUTION
Draw the FBD of the unit.

Assume impending slide requiring ![]() and write the equations of equilibrium as,
and write the equations of equilibrium as,
![Rendered by QuickLaTeX.com \[\begin{split}+\searrow\sum F_x&=0\implies F_s=W_x=W\sin\theta\\+\swarrow\sum F_y&=0\implies N=W_y=W\cos\theta\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7363b3c07e46b52cd4c2e09e4ac56712_l3.png)
With ![]() , substituting this into the equilibrium equation for F_x and solving the system of two equations lead to,
, substituting this into the equilibrium equation for F_x and solving the system of two equations lead to,
![]()
We notice that the angle of repose, ![]() , is equal to the angle of static friction.
, is equal to the angle of static friction.
To check for tipping, consider the onset of tipping at which the normal force acts at the corner of the unit as shown below.
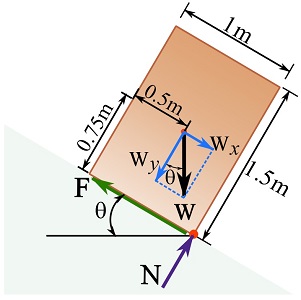
At the onset of tipping the sum of moment about any point including the corner of the unit must be zero; write the moment equilibrium about the corner of the unit as,
![]()
Solving for ![]() , we get,
, we get,
![]()
Compare ![]() and
and ![]() with each other to determine the state of the motion of the unit.
with each other to determine the state of the motion of the unit.
Because ![]() , the unit will start sliding once the inclination angle reaches
, the unit will start sliding once the inclination angle reaches ![]() .
.
Note that the magnitude of the weight of the unit was not needed to determine the slipping or tipping state of the box. The parameters directly affecting the state of the motion of the unit at a particular inclination angle are ![]() (coefficient of static friction) for sliding, and the (ratio) of width to height of the unit for tipping.
(coefficient of static friction) for sliding, and the (ratio) of width to height of the unit for tipping.
Use the following interactive tool to investigate the forces (normal and friction) and the status of the motion of a box on an inclined plane. Note that the ratio of the dimensions (width and height) of the box affects the status of the motion.
EXAMPLE 8.2.3
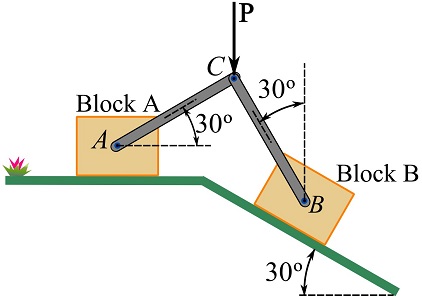
Two blocks A and B, each having the same mass of 6kg, are connected by a linkage as shown. The structure is at rest. If the coefficients of static friction at the contact surfaces are ![]() and
and ![]() , determine the largest magnitude of the vertical force
, determine the largest magnitude of the vertical force ![]() that may be applied to pin C without causing the blocks to slide. The weights of the links are negligible and the pins of the links are frictionless. Assume
that may be applied to pin C without causing the blocks to slide. The weights of the links are negligible and the pins of the links are frictionless. Assume ![]() .
.
SOLUTION
Start with drawing the FBD of the whole structure.

The direction of the frictional forces are determined based on the potential motion/slide of the boxes as shown.
To tackle this problem, the FBDs of the pin C, and the two blocks are separately considered for writing three sets of equations of equilibrium.
Pin C.

![]()
![]()
Block A.
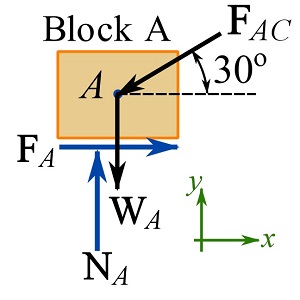
![]()
![]()
Block B.
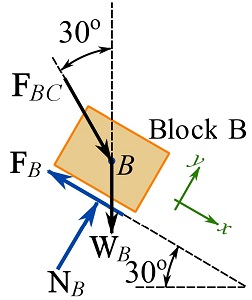
![]()
![]()
Collecting all together, we have 6 equations,
![Rendered by QuickLaTeX.com \[\begin{cases}F_{AC}\cos 30^\circ - F_{BC}\cos 60^\circ=0\\F_{AC}\sin 30^\circ + F_{BC}\sin 60^\circ -P=0\\-F_{AC}\cos 30^\circ + F_A=0\\-F_{AC}\sin 30^\circ + N_A-W_A =0\\F_{BC}\cos 30^\circ - F_B+ W_B\sin 30^\circ =0\\-F_{BC}\sin 30^\circ+ N_B-W_B\cos 30^\circ =0\end{cases}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d3c0ead99dd758d702222477ca5097e8_l3.png)
and 7 unknowns, ![]() .
.
Another equation, adding to the other six, comes from the condition on the friction. Assume that either block A or block B is about to slide, i.e. impending slide, and check the condition on the other block. Note that, it is not known which block(s) slides.
Case 1: Assume that block A is in impending slide.
In this case, ![]() . Therefore, the system of equations becomes,
. Therefore, the system of equations becomes,
![Rendered by QuickLaTeX.com \[\begin{cases}F_{AC}\cos 30^\circ - F_{BC}\cos 60^\circ=0\\F_{AC}\sin 30^\circ + F_{BC}\sin 60^\circ -P=0\\-F_{AC}\cos 30^\circ + F_A=0\\N_A-(6)(9.81) - F_{AC}\sin 30^\circ =0\\F_{BC}\cos 30^\circ + (6)(9.81)\sin 30^\circ - F_B=0\\N_B-(6)(9.81)\cos 30^\circ - F_{BC}\sin 30^\circ =0\\F_A-0.2N_A=0\end{cases}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9490104bf06156d7497a033d0e417b84_l3.png)
Solving the system of equation by substitution, we get,
![]()
Now, we need to check whether block B remains at rest or not.
Using Eqs. 5 and 6 obtained from the FBD of block B, we can write,
![]()
The maximum value that ![]() can attain is,
can attain is,
![]()
Because ![]() , block B would slide before block A is at the onset of sliding (impending slide).
, block B would slide before block A is at the onset of sliding (impending slide).
If we start with Case 2, instead of Case 1, we will have the following calculation.
Case 2: Assume that block B is in impending slide.
In this case, ![]() . Therefore, the system of equations becomes,
. Therefore, the system of equations becomes,
![Rendered by QuickLaTeX.com \[\begin{cases}F_{AC}\cos 30^\circ - F_{BC}\cos 60^\circ=0\\F_{AC}\sin 30^\circ + F_{BC}\sin 60^\circ -P=0\\-F_{AC}\cos 30^\circ + F_A=0\\N_A-(6)(9.81) - F_{AC}\sin 30^\circ =0\\F_{BC}\cos 30^\circ + (6)(9.81)\sin 30^\circ - F_B=0\\N_B-(6)(9.81)\cos 30^\circ - F_{BC}\sin 30^\circ =0\\F_B-0.8N_B=0\end{cases}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-366d8704cc071e4e572400f26709c92f_l3.png)
Solving the system of equation by substitution, we get,
![]()
Now, check the status of block A.
Using Eqs. 3 and 4 obtained from the FBD of block A, we can write,
![]()
The maximum value that ![]() can attain is,
can attain is,
![]()
Because ![]() , block A will not slide.
, block A will not slide.
Consequently, the structure is in static equilibrium under ![]() with block B in impending slide and block A is not sliding.
with block B in impending slide and block A is not sliding.
Note: although we checked for the states of the motions of both blocks in each case, we just needed to calculate ![]() in each case (either block A or block B in impending motion), without checking if the other block would slide under the calculated
in each case (either block A or block B in impending motion), without checking if the other block would slide under the calculated ![]() . The answer to the problem would be the smallest
. The answer to the problem would be the smallest ![]() of both cases.
of both cases.
Videos
Friction in Static Equilibrium:
Friction in Wheels, Wedges, and Multiple Objects:
