Engineering at Alberta Courses

Vectors and their Operations: Dot product

The dot product and its properties

The dot product, also called the scalar product, is an operation that takes two vectors and returns a scalar. The dot product of vectors $\bold A$ and $\bold B$ , denoted as $\bold A \cdot \bold B$ and read “ $\bold A$ dot $\bold B$ ” is defined as:

(2.14) $\bold A\cdot\bold B=|\bold A||\bold B|\cos \theta$

where $0^\circ\le \theta \le 180^\circ$ is the angle between the two vectors (Fig. 2.24)

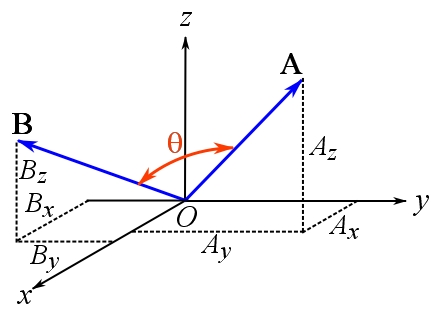
Figure 22. Configuration of two vectors for the dot product. — Fig. 2.24 Configuration of two vectors for the dot product.

From the definition, it is obvious that the result of the dot product is a scalar. The dot product has three properties as follows:

Commutativity: $\bold A\cdot\bold B = \bold B\cdot\bold A$
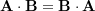
Associativity (scalar multiplication): $c(\bold A\cdot\bold B)=(c\bold A)\cdot \bold B=\bold A\cdot(c\bold B)=(\bold A\cdot\bold B)c$
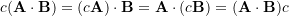
Distributivity: $\bold A\cdot(\bold B + \bold D)=(\bold A\cdot \bold B)+(\bold A\cdot\bold D)$

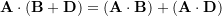
The proofs of the first two properties are by direct use of the dot product definition (Eq. 2.14). The proof for the third property is by expanding the right hand side of the equation using CVN and using the properties explained below.

Other properties of the dot product

Dot product of a vector by itself gives its squared magnitude: $\bold A\cdot \bold A=|\bold A|^2$ .
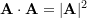Dot product of two perpendicular vectors is zero: $\theta=90^\circ \Rightarrow \bold A\cdot \bold B=0$ .
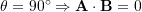Dot product by the zero vector is zero: $\bold A\cdot \bold 0=0$ .

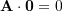These properties can be easily proved using Eq. 2.14.

Formulation of the dot product using CVN

Let $\bold A$ and $\bold B$ be two vectors with their scalar components $(A_x, A_y, A_z)$ and $(B_x, B_y, B_z)$ . Using CVN, we can write:

$\begin{split} \bold A\cdot \bold B&=(A_x\bold i +A_y\bold j+A_z\bold k )\cdot(B_x\bold i +B_y\bold j+B_z\bold k)\\ &\text{by the distributivity property}\\ &=A_xB_x(\bold i\cdot \bold i)+A_xB_y(\bold i\cdot \bold j)+A_xB_z(\bold i\cdot \bold k)\\ &+A_yB_x(\bold j\cdot \bold i)+A_yB_y(\bold j\cdot \bold j)+A_yB_z(\bold j\cdot \bold k)\\ &+A_zB_x(\bold k\cdot \bold i)+A_zB_y(\bold k\cdot \bold j)+A_zB_z(\bold k\cdot \bold k) \end{split}$

The dot product of the unit vectors, by the dot product properties, are:

$\begin{split} \bold i \cdot \bold i&=\bold j \cdot \bold j=\bold k \cdot \bold k=1\\ \bold i \cdot \bold j&=\bold j \cdot \bold i=\bold i \cdot \bold k=\bold k \cdot \bold i=\bold j \cdot \bold k=\bold k \cdot \bold j=0 \end{split}$

Therefore,

(2.15) $\bold A\cdot \bold B=A_xB_x+A_yB_y+A_zB_z$

This result expresses that the dot product of two vectors written in their CVN can be obtained by multiplying their corresponding scalar components and summing over these products algebraically. Equation 2.15 indicates that calculating the dot product (Eq. 2.14) does not need the magnitudes of two vectors and the angle between them, if the vectors are expressed in CVN.

Application of the dot product: finding the angle between two vectors

The dot product can be used to find the angle formed between two vectors or two intersecting lines. This is helpful particularly when solving problems in three dimensions. The angle between two vectors is obtained by solving Eq. 2.14 for the angle term:

(2.16) $\begin{split}\theta&=\cos^{-1}(\frac{\bold A\cdot\bold B}{|\bold A||\bold B|})\quad 0^\circ\le \theta\le 180^\circ\\\bold A&\cdot \bold B=A_xB_x+A_yB_y+A_zB_z \end{split}$

The above equation can be manipulated as:

(2.17) $\theta=\cos^{-1}(\frac{\bold A}{|\bold A|}\cdot\frac{\bold B}{|\bold B|})=\cos^{-1}(\bold u_A\cdot\bold u_B)\quad 0^\circ\le \theta\le 180^\circ$

in which $\bold u_a$ and $\bold u_b$ are the unit vectors of $\bold A$ and $\bold B$ respectively. This result naturally states that the angle between two vectors only depends on their directions and not on their magnitudes.

Application of the dot product: orthogonal projection of a vector

In many problems, we need to resolve a vector on a particular line or lines in the space. To be more precise, the component of a vector along a particular direction or axis is to be found. Decomposing a vector onto the Cartesian axes is already demonstrated. In this section, we explain decomposing a vector on a general line in space using the dot product. Using the dot product makes the calculation easier specially in three dimensions.

Consider a non-zero vector $\bold A$ in the three dimensional space and a line $l$ intersecting the tail of the vector at a point $O$ (Fig. 2.25a). A unit vector $\bold u$ is associated with line $l$ to assign a direction to the line. In other words, The positive direction of the line is determined by $\bold u$ . As demonstrated in Fig. 2.25b, the vector $\bold A$ can be written as,

(2.18) $\bold A =\bold A_{\parallel} + \bold A_{\perp}$

where $\bold A_{\parallel}$ is parallel to $\bold u$ , and $\bold A_{\perp}$ is perpendicular to $\bold u$ . The symbols $\parallel$ and $\perp$ denote being parallel and perpendicular respectively.

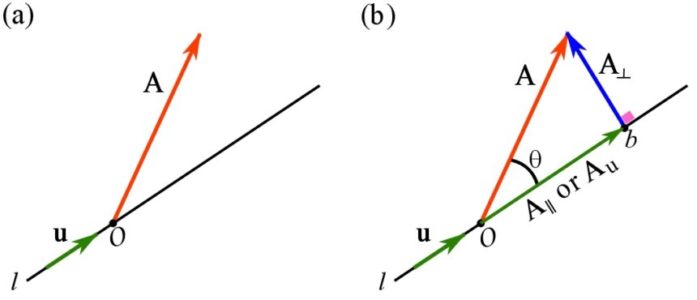
Fig. 2.24. Orthogonal projection. — Fig. 2.25 Orthogonal projection.

The vector $\bold A_{\parallel}$ is referred to as the orthogonal projection (or projection) of $\bold A$ onto the line $l$ or along the direction of $\bold u$ . We denote $\bold A_{\parallel}$ as $\bold A_u$ to indicate that $\bold A_{\parallel}$ is a projection along the direction of $\bold u$ .

To obtain $\bold A_u$ , it suffices to note that the vectors $\bold A$ , $\bold A_u$ and $\bold A_{\perp}$ form a right-angle triangle (Fig. 2.25b). Therefore by the Pythagorean’s theorem $|\bold A_u|=|\bold A|\cos \theta$ . This inspires us to use Eq. 2.14 and write,

(2.19) $\begin{split} A_u=|\bold A|\cos \theta&=\bold A\cdot\bold u \\\implies \bold A_u&=A_u\bold u \end{split}$

It should be noted that $A_u$ is the scalar component of $\bold A$ resolved along the direction of $\bold u$ . Using the dot product $\bold A \cdot \bold u$ to calculate $A_u$ may result in a negative scalar if the angle between $\bold A$ and $\bold u$ are larger than $90^\circ$ . In such a case, the direction of $\bold A_u$ is in the opposite direction of $\bold u$ .

The following interactive tool illustrates the orthogonal projection of a vector $\bold A$ on the direction defined by a unit vector $\bold u$ .

The perpendicular component of $\bold A$ can be then obtained by writing,

(2.20) $\bold A_{\perp}=\bold A-\bold A_u$

The magnitude of the perpendicular component can be calculated either by $|\bold A_\perp|=|\bold A|\sin \theta$ or $|\bold A_\perp|=\sqrt{|\bold A|^2-|\bold A_u|^2}$ .

In practice, $|\bold A_u|=|\bold A|\cos \theta$ and $|\bold A_\perp|=|\bold A|\sin \theta$ can be readily used if $\theta$ in known, otherwise $A_u=\bold A\cdot\bold u$ , $\bold A_{\perp}=\bold A-\bold A_u$ , and $|\bold A_\perp|=\sqrt{|\bold A|^2-|\bold A_u|^2}$ can be utilized if the components of the vectors in CVN are known.