Vectors and their Operations: Scalars and vectors
Scalars and vectors are mathematical objects that are used to quantify physical quantities.
Scalar. A scalar is a real number. For example ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and so on .
, and so on .
Scalar quantity. A scalar quantity is a quantity that can be described by a single real number. This number specifies the magnitude or size of that quantity. For example length, angle, mass, speed, area, temperature, and pressure are scalar quantities.
Sometimes a scalar quantity is simply referred to as scalar. For example, “mass is a scalar” is equivalent to stating: “mass is a scalar quantity”.
The mathematical operations on scalars follow the usual rules of arithmetic.
Vector. A vector is a mathematical object that has a size (magnitude) and a direction. This definition perfectly fulfills the requirements of engineering mechanics. However, for a more rigorous mathematical definition click here.
Vector quantity. A vector quantity is a quantity characterized by both a magnitude and a direction. For example velocity, force, acceleration, and moment are all vector quantities.
The magnitude (sometimes referred to as the norm) of a vector is a positive scalar. For example the magnitude of the velocity of a moving object is the speed of that object. Speed is always measured and reported as a positive number. The magnitude of a physical quantity must have a unit.
The terms vector and vector quantity can be interchangeably used.
In this book, we distinguish between a vector and a scalar using special notations. The notation for a vector is a bold upper-case letter ![]() or an upper-case letter with a symbolic overhead arrow
or an upper-case letter with a symbolic overhead arrow ![]() . By convention, the direction of the arrow is from left to right and it does not convey any information about the direction of the vector itself. Using an upper-case letter with a symbolic overhead arrow is recommended when writing notes, assignments, or exams. The magnitude of a vector is denoted by the vector notation embedded by two vertical lines
. By convention, the direction of the arrow is from left to right and it does not convey any information about the direction of the vector itself. Using an upper-case letter with a symbolic overhead arrow is recommended when writing notes, assignments, or exams. The magnitude of a vector is denoted by the vector notation embedded by two vertical lines ![]() or
or ![]() . The embedding vertical line notation is also used to denote the absolute value of a scalar, for example
. The embedding vertical line notation is also used to denote the absolute value of a scalar, for example ![]() where
where ![]() is a real number. In some text the notation of vector magnitude is a double-vertical-line notation
is a real number. In some text the notation of vector magnitude is a double-vertical-line notation ![]() and the absolute value of a scalar is shown by
and the absolute value of a scalar is shown by ![]() . In this book,
. In this book, ![]() is used for both cases. The double-vertical-line notation is reserved for a later use.
is used for both cases. The double-vertical-line notation is reserved for a later use.
Context: Scalars and Vectors
- Engineers work with scalars and vectors on a daily basis.
- The two types of vectors that we will consider in ENGG 130 are forces (vectors that push or pull) and moments (vectors that twist or bend). More detailed definitions of forces and moments will be given in Chapter 3 of this book.
- In future courses, you will encounter other vector quantities such as electric fields.
Using statics principles covered over the course of this book, engineers determine the magnitude and direction of force and moment vectors that act on objects (e.g. building columns, bridge girders, airplane wings, car axles). - The magnitude and direction of forces and moments are major factors that influence the size and material of engineered members.
Applications: why are both magnitude and direction important?
Consider the stadium (BC Place) shown in Fig. 2.1. The stadium’s roof is held up by a series of cables arranged around the building’s perimeter. Engineers use statics to determine how much force (i.e. magnitude) each cable carries to hold up the weight of the roof along with additional forces caused by factors like wind and snow. Knowing the magnitude of forces in the cables allows engineers to determine how large the cables need to be to prevent them from snapping.
Cables are strong in tension (i.e. pulling forces) but are very weak in compression (i.e. pushing forces) so engineers need to not only know the magnitude of forces but also which direction they act.
Using equilibrium concepts (discussed in more detail in Chapter 5 of this book), engineers balance tension forces with compression forces. In BC Place, diagonal ‘struts’ are designed to carry compression forces induced by tension in the cables (arising from Newton’s 3rd Law). The struts need to be considerably larger than the cables because long members that carry compression forces are sensitive to buckling (a phenomenon you can observe for yourself if you push on a ruler from both ends).

Fig. 2.1 Roof of BC Place Stadium, Vancouver (Photo by D. Tomlinson)
Graphical representation of vectors
Prior to explaining the graphical representation of a vector, two geometrical objects, which are a line segment and a directed line segment, should be defined.
A line segment is a finite-length piece of a straight line. It is defined by the segment embedded between two points on a straight line. A line segment has a definite length which can be regarded as its magnitude.
A directed line segment (arrow) is a line segment with a defined direction. To define the direction, one of the segment’s end point is distinguished as the tail, and consequently the other one as the head. Thereby, the direction is defined as the sense of moving from the tail to the head of the segment. A directed line segment can be displayed by an arrow such that the arrow head defines the sense of direction.
A graphical or geometrical representation of a vector is by a directed line segment or an arrow. An arrow has both a magnitude and a direction which are the properties defining a vector. Therefore, an arrow is a vector. To be more precise an arrow is a geometric vector.
The line that is collinear with an arrow is called the line of action. The orientation or direction of an arrow (its tail is already known or defined) with respect to a fixed axis is defined by an angle formed between the axis and the line of action of the arrow. Figure 2.2 shows a directed line segment or arrow representing the vector ![]() with its defined terms.
with its defined terms.
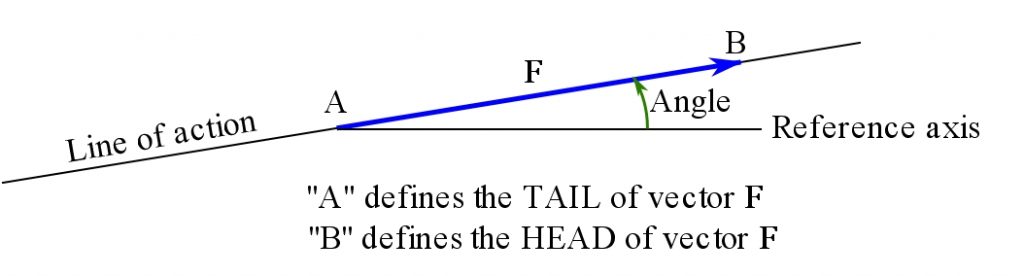
Fig. 2.2 Geometric representation of a directed line segment (arrow) or a vector.
Zero vector. The zero vector, denoted by ![]() or
or ![]() , is a vector of length zero. The zero vector does not point toward any direction, therefore, its direction is undefined.
, is a vector of length zero. The zero vector does not point toward any direction, therefore, its direction is undefined.
It should be noted that a vector (directed line segment) is defined by only two parameters being magnitude and direction. Therefore, the position of a vector in the space does not change the properties. As a result, two vectors are equal if they have the same direction and magnitude. Examples of equal vectors are shown in Fig 2.3a.
Parallel vectors. Two vectors are parallel if they have parallel lines of action. In other words, two parallel vectors have the same or opposite sense of directions. Examples of parallel vectors are shown in Fig. 2.3b.
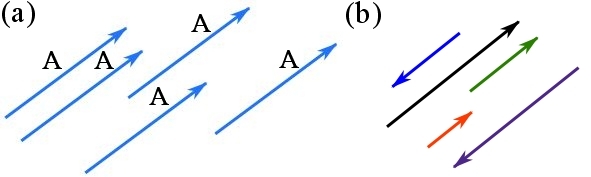
Fig. 2.3 (a) equal vectors, (b) parallel vectors
This geometric representation applies to vectors in one-dimension (along a line), a plane (a two-dimensional space) or in a three-dimensional space.
