Engineering at Alberta Courses » Vector components

Vectors and their Operations: Vector components

If $\bold F=\bold F_1+\bold F_2$ , it implies that $\bold F$ has two components along the directions or lines of action of $\bold F_1$ and $\bold F_2$ (Fig. 2.13). We can consider decomposing the vector $\bold F$ into two vector components $\bold F_1$ and $\bold F_2$ . Given a set of two directions, a unique component of a vector along each direction can be found by decomposing the vectors. Vector decomposition of $\bold F$ can be regarded as the reverse of the vector addition, which means finding vectors with known directions (but unknown magnitude) such that their addition equals $\bold F$ . Decomposing a vector can be performed using the parallelogram rule and trigonometry laws.

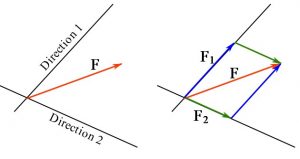
Fig. 2.13 Decomposing a (planar) vector into two components along two directions or lines.

Vector decomposition produces components of vectors that are parallel with particular axes. The following interactive example shows the process of vector decomposition.

EXAMPLE 2.3.1

The vector $\bold F$ of magnitude $\vert \bold F\vert = 100$ is to be resolved into two components along the lines $u$ and $v$ . Determine the angle $\alpha$ if the component of $\bold F$ along the line $v$ has a magnitude of $70$ , i.e. $\vert \bold F_v\vert = 70$ .

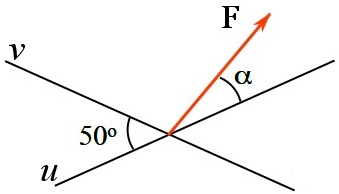
SOLUTION

Use the parallelogram rule on the given directions of the component vectors.

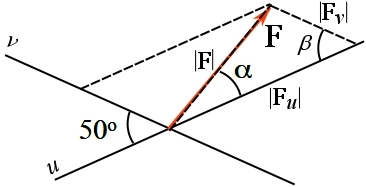
$\angle \beta = 50^{\circ}$ because of the parallel sides.

From Sine Law,

$\begin{split}\frac{\sin{\alpha}}{|\bold F_{v}|}&= \frac{\sin{\beta}}{|\bold F|}\\\frac{\sin{\alpha}}{70} &= \frac{\sin{50^{\circ}}}{100}\\\alpha &= 32.4^{\circ}\\\end{split}$

EXAMPLE 2.3.2

Determine the resultant vector, $\bold R = \bold P + \bold Q$ .

SOLUTION

Two methods:

Method 1

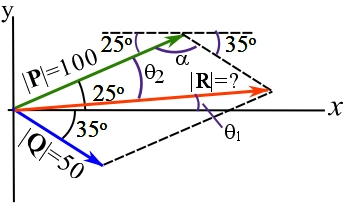
From geometry: $180^{\circ}=25^{\circ}+35^{\circ}+\alpha\ \Rightarrow\ \alpha=120^{\circ}$ .

From Cosine Law: $|\bold R|^2=100^{2}+50^{2}-2(100)(50)\cos{120^{\circ}}\ \Rightarrow\ |\bold R|=132.3$ .

From Sine Law: $\large\frac{50}{\sin{\theta_{2}}}=\frac{132.2}{\sin{120^{\circ}}}\ \Rightarrow\ \theta_{2}=19.10^{\circ}$ .

Answer: $|\bold R|=132.3$ , $\theta_1= 5.90^{\circ}$

parallelogram method, the use of Sine and Cosine laws is cumbersome. To add vectors efficiently systematically, vectors can be decomposed (resolved) onto a set of common directions and the resulting parallel vector components can be simply added.

Method 2

By decomposing the vectors $\bold P$ and $\bold Q$ on the two perpendicular lines (axes) denoted as x and y.

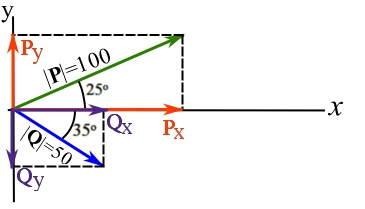
Components of $\bold P$ are as,

$\begin{split}\bold P&=\bold P_x+\bold P_y\\|\bold P_x|&=|\bold P|\cos 25^ \circ=90.6\\|\bold P_y|&=|\bold P|\sin 25^\circ=42.3\end{split}$

Components of $\bold{Q}$ are as,

$\begin{split}\bold Q&=\bold Q_x+\bold Q_y\\|\bold Q_x|&=|\bold Q|\cos 35^ \circ =41.0\\|\bold Q_y|&=|\bold Q|\sin 35^\circ=28.7\end{split}$

Solving for $\bold{R}$ :

$\begin{split}\bold R&=\bold P+\bold Q\\&=(\bold P_x+\bold P_y)+(\bold Q_x+\bold Q_y)=(\bold P_x+\bold Q_x)+(\bold P_y+\bold Q_y)\\&=\bold R_x + \bold R_y \\&|\bold R_x|=|\bold P_x|+|\bold Q_x| = 131.6 \\&|\bold R_y|=|\bold P_y| - |\bold Q_y| = 13.6\end{split}$

Therefore:

$\begin{split}|\bold R|&=\sqrt{|\bold R_x|^2+|\bold R_y|^2}=132\\\tan \theta_1 &=\frac{|\bold R_y|}{|\bold R_x|}=\frac{13.6}{131.6}\\ &\implies \theta_1=5.9^{\circ}\end{split}$

Answer: $|\bold{R}|=132.3$ , $\theta_1=5.9^{\circ}$

In the above example, the vectors are resolved into their components on the given axes and the parallel components of the vectors are added. Then, adding the resultant vectors on the axes gives the final resultant vector. This approach is a systematic approach for adding vectors.