Problems: Chapter 5
1- Determine the support reactions and the force in the cable.
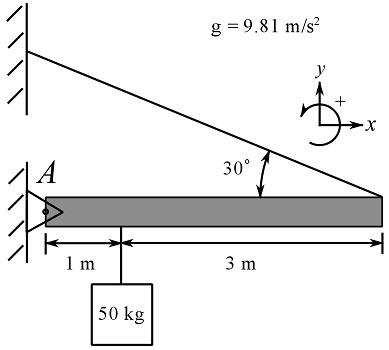
Answer
![]()
2- Determine the Support Reactions.
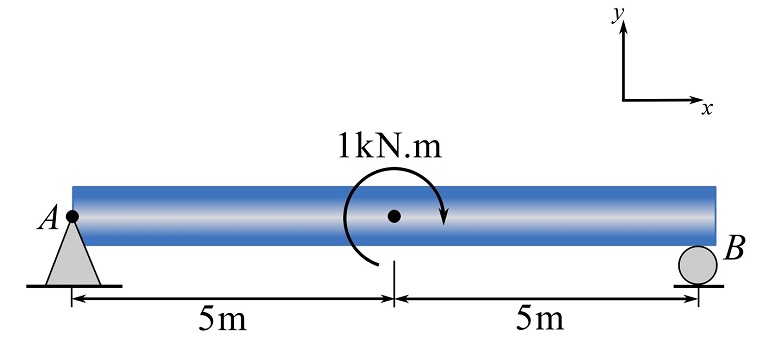
Answer
![]()
3- Determine the magnitudes of the cable forces for the two cases shown.
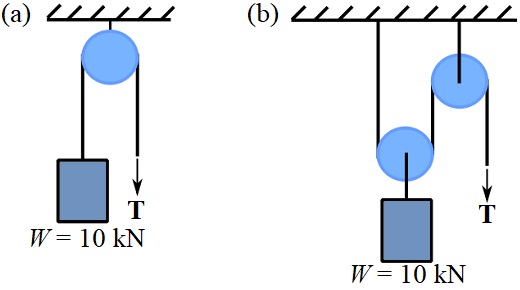
Answer
Case (a): ![]() . Case (b)
. Case (b) ![]()
4- Determine the support reactions.
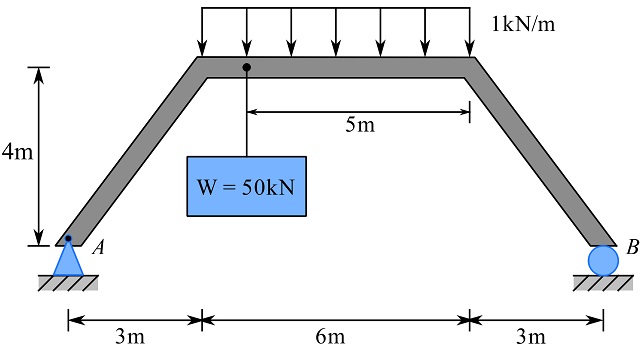
Answer
![]()
5- Determine the support reactions. Express the support reactions in the direction of the Cartesian axes x and y shown at the support.

Answer
![Rendered by QuickLaTeX.com \[\begin{split}A_x &= 15\text{ kN}\nearrow \\A_y &= 20\text{ kN}\nwarrow\\M_A &= 183\text{ kN.m}\circlearrowleft\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-feebd7f6d16be820e7d73e7d79756f31_l3.png)
6- A structure (frame) is supported by the ground as shown. The soil under the supports of the structure can resist a maximum pressure of ![]() . If the area of each foundation under each support of the structure is
. If the area of each foundation under each support of the structure is ![]() , determine the maximum intensity (
, determine the maximum intensity (![]() ) of the load (applied over the span of the structure) that does not cause pressure higher than the maximum permissible pressure of the soil under the supports (foundations). Assume that the pressure caused by the foundations is uniformly distributed on the soil underneath.
) of the load (applied over the span of the structure) that does not cause pressure higher than the maximum permissible pressure of the soil under the supports (foundations). Assume that the pressure caused by the foundations is uniformly distributed on the soil underneath.

Answer
![]()
7- Determine the support reactions.
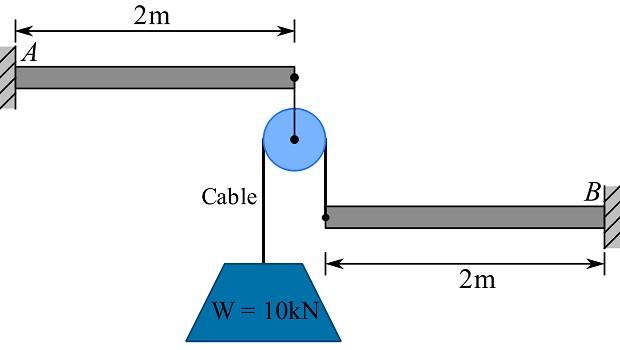
Answer
![]()
8- Determine the support reactions.
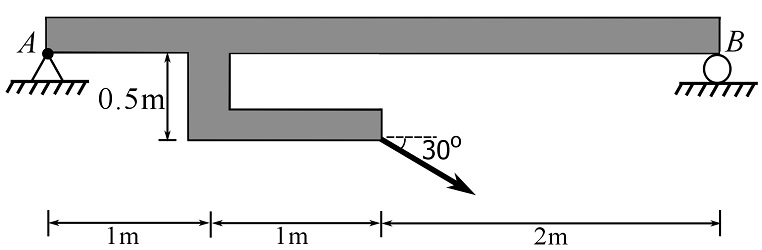
Answer
![]()
9- Determine the support reactions.

Answer
![]()
