Moments of Inertia of area: Parallel axis theorem
In many cases, the moment of inertia about an axis, particularly an axis passing through the centroid of a common shape, is known (or relatively easier to calculate) and the moment of inertial of the area about a second axis parallel to the first axis is needed. The parallel axis theorem relates these two moments of inertia.
To derive the theorem, an area as shown in Fig. 10.9 is considered. The centroid of the area is denoted as ![]() , the
, the ![]() axis is an axis crossing the centroid (a centroidal axis), and the
axis is an axis crossing the centroid (a centroidal axis), and the ![]() axis is an arbitrary axis parallel to
axis is an arbitrary axis parallel to ![]() .
.
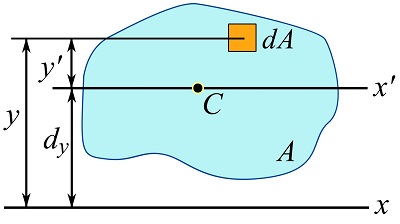
If ![]() is a differential element of the area, its (perpendicular) distance to the
is a differential element of the area, its (perpendicular) distance to the ![]() axis can be written as
axis can be written as ![]() where
where ![]() is the distance between the two parallel axes shown in Fig. 10.9. Therefore,
is the distance between the two parallel axes shown in Fig. 10.9. Therefore,
![Rendered by QuickLaTeX.com \[\begin{split}I_x & = \int_A y^2 dA=\int_A (d_y+y')^2dA\\&=\int_A d_y^2dA + \int_A y'^2dA+\int_A 2d_y y'dA\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-071ec45b0506b4fefd523b1b6fe61ac7_l3.png)
The term ![]() equals zero because
equals zero because ![]() and
and ![]() (measured from the
(measured from the ![]() axis) because
axis) because ![]() passes through the centroid. Consequently,
passes through the centroid. Consequently,
![]()
With ![]() and
and ![]() , then
, then
(10.7) ![]()
which reads the moment of inertia about an axis ![]() is equal to the moment of inertia about a parallel axis
is equal to the moment of inertia about a parallel axis ![]() that crosses the centroid of
that crosses the centroid of ![]() , plus the product of area
, plus the product of area ![]() and the square distance between
and the square distance between ![]() and
and ![]() .
.
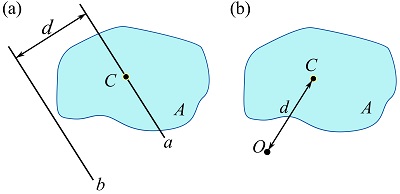
Equation 10.7 can be written for any two parallel axes with one crossing the centroid of the area. If ![]() is an axis crossing
is an axis crossing ![]() , and
, and ![]() a parallel axis to
a parallel axis to ![]() as shown in Fig. 10.10a, we can write,
as shown in Fig. 10.10a, we can write,
(10.8) ![]()
where ![]() is the distance between the two parallel axes.
is the distance between the two parallel axes.
The parallel axis theorem also hold for the polar moment of inertia. If ![]() is a point in the plane of an area and distant
is a point in the plane of an area and distant ![]() from the centroid
from the centroid ![]() of the area as shown in Fig. 10.10b, the polar moments of inertia about
of the area as shown in Fig. 10.10b, the polar moments of inertia about ![]() and
and ![]() are related as,
are related as,
(10.9) ![]()
EXAMPLE 10.3.1
Determine the moment of inertia of a rectangular area about the x and y axes shown. Use the moment of inertia about the centroidal axes parallel to its sides.
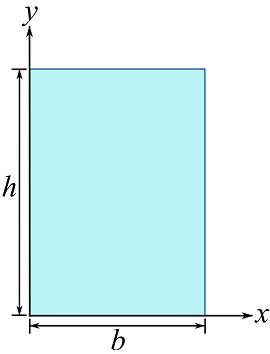
SOLUTION
Let ![]() and
and ![]() be two axes crossing the centroid of the area as shown. According to Example 10.1.1,
be two axes crossing the centroid of the area as shown. According to Example 10.1.1,
![]()
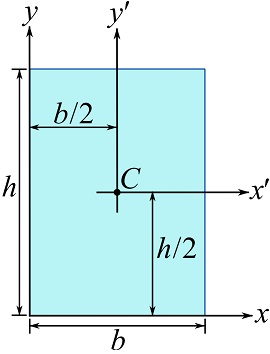
Therefore, by Eq. 10.8, we can write,
![]()
And,
![]()
EXAMPLE 10.3.2
If ![]() for the depicted triangular area, determine the moment of inertia about the axis crossing the centroid of the area and parallel to the x axis.
for the depicted triangular area, determine the moment of inertia about the axis crossing the centroid of the area and parallel to the x axis.
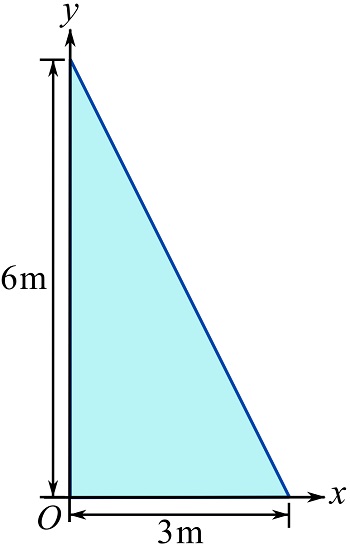
SOLUTION
Find the distance from the x axis to the centroid of the area, and use Eq. 10.8.
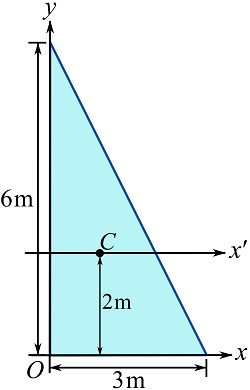
![]()
Therefore,
![]()
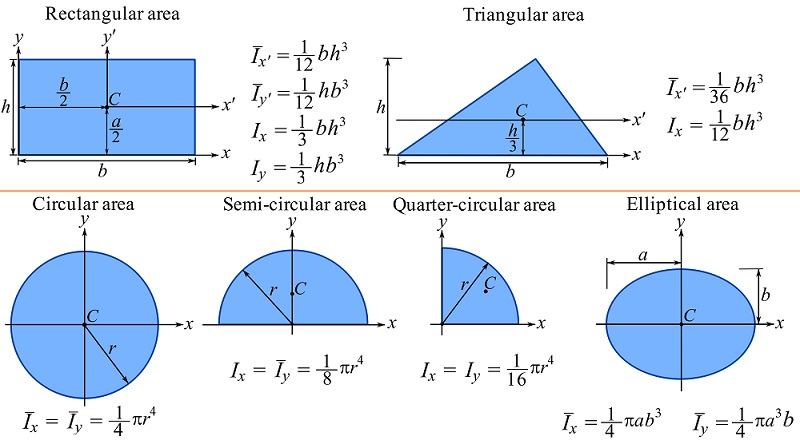
Figure 10.11 demonstrates some basic areas and the formulations of their moments of inertia (see this document for some other areas).