Vectors and their Operations: Cross product
The cross product and its properties
The cross product of two vectors is an operation that takes two vectors 
and 
and returns a vector 
. This operation is denoted by 
and is read “C equals A cross B”. The magnitude of 
is defined as,
(2.22) ![\[|\bold C|=|\bold A||\bold B|\sin\theta,\quad 0\le\theta \le 180^\circ\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a39fd4582ea6daba677dbe02b1310d16_l3.png "Rendered by QuickLaTeX.com")
in which 
is the angle between the two vectors.
The definition of the magnitude of the cross product implies that, 
if two non-zero vectors are parallel.
By definition, is perpendicular to both and , which are not parallel, and its sense of direction is specified by the right-hand rule. In other words, is perpendicular to the plane containing the non-parallel vectors and such that (or 
) is in the direction of the thumb following the right-hand rule (Fig. 2.26a). The right-hand rule can also be equivalently demonstrated by the right-hand three-finger rule as demonstrated in Fig. 2.26b.
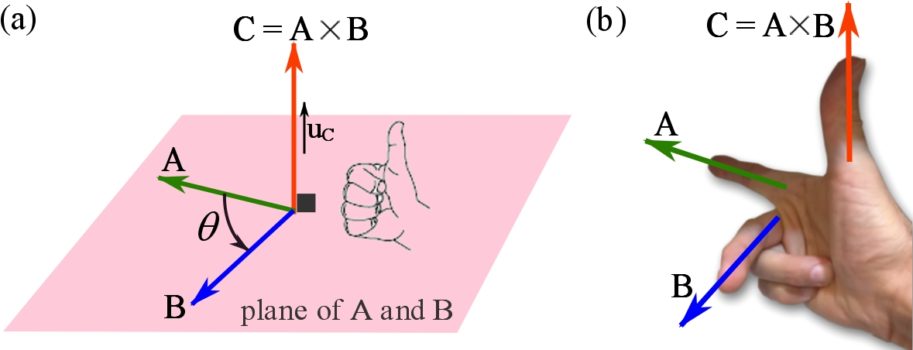
If is the unit vector of , the resultant of a cross product 
can be written as,
(2.23) ![\[\bold C = \bold A\times\bold B=|\bold A||\bold B|\sin \theta\ \bold u_C \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ef1eec16521e92925acfc57bdf18cdb6_l3.png "Rendered by QuickLaTeX.com")
The following interactive tool illustrates 
. Use the sliders to change the angles of and with the Cartesian axes, and observe the resultant of their cross product.
Properties of Cross product
- Anti-commutativity:
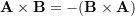
- Associativity: for
being a scalar, 
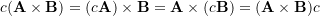
- Distributivity:
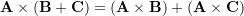
Cross product in CVN
In a Cartesian frame the following relationships are readily obtained for the mutually perpendicular unit vectors 
, 
and 
.
(2.24) ![\[ \begin{matrix} \bold i\times \bold i=\bold 0 &\bold i\times \bold j=\bold k & \bold i\times \bold k=-\bold j \\ \bold j\times \bold i=-\bold k & \bold j\times \bold j=\bold 0 & \bold j\times \bold k=\bold i \\ \bold k\times \bold i=\bold j & \bold k\times \bold j=-\bold i & \bold k\times \bold k=\bold 0 \end{matrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-14b8530a57bbaf2b85b6afc467425e0c_l3.png "Rendered by QuickLaTeX.com")
Based on the above results and the properties of the cross product, the cross product of two vectors in their CVN is,
![\[ \begin{split} \bold A&=A_x\bold i + A_y\bold j+A_z\bold k\quad , \quad \bold B=B_x\bold i+B_y\bold j+B_z\bold k\\\bold C = \bold A\times \bold B&=(A_xB_x)\bold i\times \bold i +(A_xB_y)\bold i\times \bold j +(A_xB_z)\bold i\times \bold k\\&+(A_yB_x)\bold j\times \bold i +(A_yB_y)\bold j\times \bold j +(A_yB_z)\bold j\times \bold k \\&+(A_zB_x)\bold k\times \bold i +(A_zB_y)\bold k\times \bold j +(A_zB_z)\bold k\times \bold k \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-06c212c9e16c04abaa6d0c318e9dd3b3_l3.png "Rendered by QuickLaTeX.com")
leading to,
(2.25) ![\[ \bold C = \bold A\times\bold B=(A_yB_z-A_zB_y)\bold i+(A_zB_x-A_xB_z)\bold j+(A_xB_y-A_yB_x)\bold k \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1a5248ebe83a33271c53a66b46c25b77_l3.png "Rendered by QuickLaTeX.com")
This result need not to be memorized and can be obtained by calculating the following determinant symbolically.
(2.26) ![\[\bold A\times\bold B = \left\|\begin{matrix} \bold i & \bold j & \bold k \\ A_x & A_y & A_z \\ B_x & B_y & B_z \\ \end{matrix}\right\|\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1335c22037e5eba4719310eb1b70ef71_l3.png "Rendered by QuickLaTeX.com")
As a reminder, the determinant of a two-by-two matrix 
is a scalar defined as,
![\[M=\begin{bmatrix}a && b\\ c && d\end{bmatrix}\implies\|M\|=ad-bc\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-31b2eb7dbd07f063ee81bbaf631b4745_l3.png "Rendered by QuickLaTeX.com")
Consequently, the determinant of a three-by-three matrix is a scalar defined as
![\[M=\begin{bmatrix}a && b && c\\ d && e && f \\ g && h && i\end{bmatrix}\implies\|M\|=a\left\|\begin{matrix} e & f \\ h & i \end{matrix}\right\| - b\left\|\begin{matrix} d & f \\ g & i \end{matrix}\right\| + c\left\|\begin{matrix} d & e \\ g & h \end{matrix}\right\|\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-251157da36dda50196edd8fc9993592d_l3.png "Rendered by QuickLaTeX.com")
The following tool calculates the cross product 
. The vector is drawn in green.