Review of single and multi-degree of freedom (mdof) systems: Vibration and Applications of MDOF Systems
For more than a SDOF system the analysis requires a more generalized approach. However, overall it doesn’t matter if there are 2 or 22 DOFs. Consider first a special 2 DOF free vibration system:
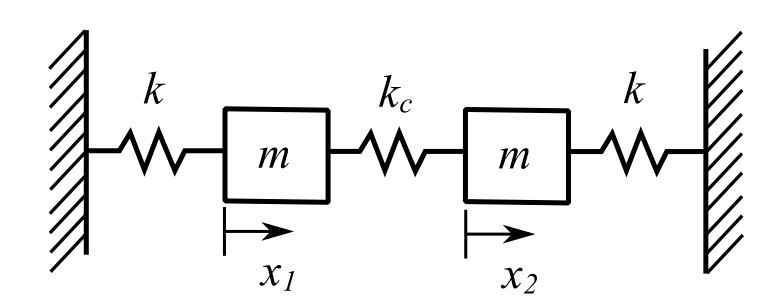
![]()
The simplest approach is to look for Simultaneous Simple Harmonic Motion (SSHM). That is:
![]()
Which is a solution (not the general one) if:
![]()
This can be true if and only if (iff), ![]() . Therefore:
. Therefore:
![]()
There are two soloutions for ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{split} p_{1,2}^2 &= \frac{k+k_c}{m} \pm \sqrt{\frac{k^2+2kk_c + k_c^2 - (k^2 + 2kk_c)}{m^2}} \\&= \frac{k+k_c}{m} \pm \frac{k_c}{m} \\&= \frac{k}{m}, \ \frac{k+2k_c}{m} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-634f829480b55d4f948d3d5022accc12_l3.png)
Therefore:
![]()
As a result, there are 2 frequencies at which our assumption is true. NOTE: It turns out that the general solution can be determined from these ![]() ,
, ![]() , and the ratio of the amplitudes between the two masses during each of the two SSHMs. Therefore:
, and the ratio of the amplitudes between the two masses during each of the two SSHMs. Therefore:
![]()
Or:
![]()
Therefore, for either ![]() or
or ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{X_2}{X_1} &= \frac{k +k_c -mp^2}{k_c} \\&= \frac{k_c}{k+k_c-mp^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-328e44d8a089158705e8ee12c0d62183_l3.png)
If we put ![]() into either we get:
into either we get:
![]()
And if we put ![]() into either we get:
into either we get:
![]()
Thus, we define the mode shapes corresponding to each ratio:
![]()
![]()
Therefore, we have a mode shape corresponding to each of the natural frequencies. ![]() and
and ![]() are “normalized” vectors where the first component is set arbitrarily to unity. The general solution to the free vibration problem is then:
are “normalized” vectors where the first component is set arbitrarily to unity. The general solution to the free vibration problem is then:
![]()
There are 4 constants ![]() ,
, ![]() ,
, ![]() ,
, ![]() for the 4 initial conditions for
for the 4 initial conditions for ![]() ,
, ![]() ,
, ![]() ,
, ![]() . If the initial conditions are selected then the solution will include both modes in general but only one mode for certain cases. (For example, when
. If the initial conditions are selected then the solution will include both modes in general but only one mode for certain cases. (For example, when ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
, ![]() mode 1).
mode 1).
Consider the following initial conditions:
![]()
![]()
![]()
At ![]() :
:
![]()
![]()
![]()
![]()
Therefore:
![]()
![]()
Therefore:
![]()
From (1) and (2) (+):
![]()
![]()
From (1) and (2) (-):
![]()
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} x_1 &= \frac{1}{2}\sin\Big(p_1t + \frac{\pi}{2}\Big) + \frac{1}{2}\sin\Big(p_2t + \frac{\pi}{2}\Big) \\&= \frac{1}{2}\cos p_1t + \frac{1}{2}\cos p_2t \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7c2c85accd5775261cf0d4d13e2843c4_l3.png)
![]()
Using identities:
![]()
![]()
These may be interpreted as a higher frequency oscillation at the average of the two natural frequencies with a variable amplitude, given by a lower frequency given by ![]() the difference in natural frequencies.
the difference in natural frequencies.
If ![]() and
and ![]() are close to each relative to their magnitude then
are close to each relative to their magnitude then ![]() , the motion becomes:
, the motion becomes:
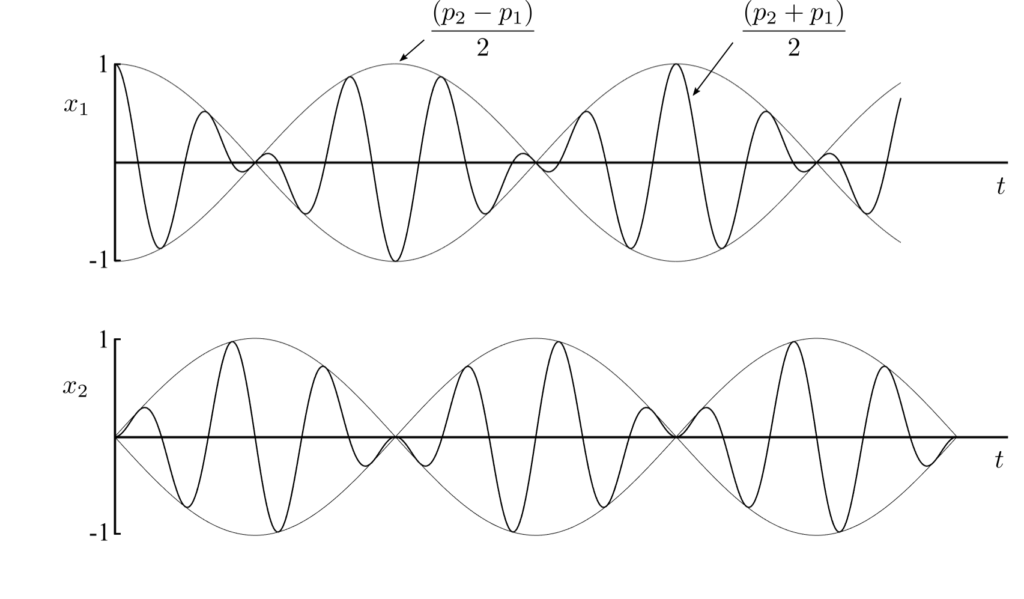

if sinx(x)=-cos(x+pi/2)
Could it be x1 and x2 negative?
Sorry
sin(x)=-cos(x+pi/2)
Ok.I’m wrong
sin(x+pi/2)=cos(x)
Could it be x1 and x2 were positive
Thanks a lot for the classes.
Best regards