Open Educational Resources

Review of single and multi-degree of freedom (mdof) systems: Stiffness and Flexibility Influence Coefficients

We can use the Newtonian approach to find the stiffness matrix and equations of motion. However, we can also use influence coefficients for both the mass and stiffness matrices.

Consider the definition of stiffness and flexibility influence coefficients:

S.I.C

k_{ij} is the force (moment) required at coordinate i to maintain a unit linear (angular) displacement at coordinate j with all other coordinates held fixed at zero

F.I.C

a_{ij} is the linear (angular) displacement at coordinate i due to a unit force (moment) applied at coordinate j with all other coordinates free to move.

NOTE: All forces (moments) and displacements (rotations) are taken to be applied in the positive direction. The sign of the resulting forces (moments) or displacements (rotations) are determined to be positive or negative.

Also note that:

    \[ [a_{ij}]^{-1} = [k_{ij}] \]

Example

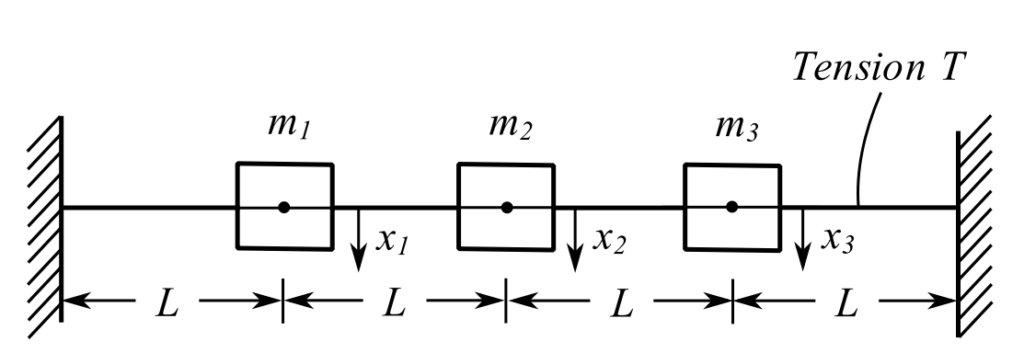
Stiffness

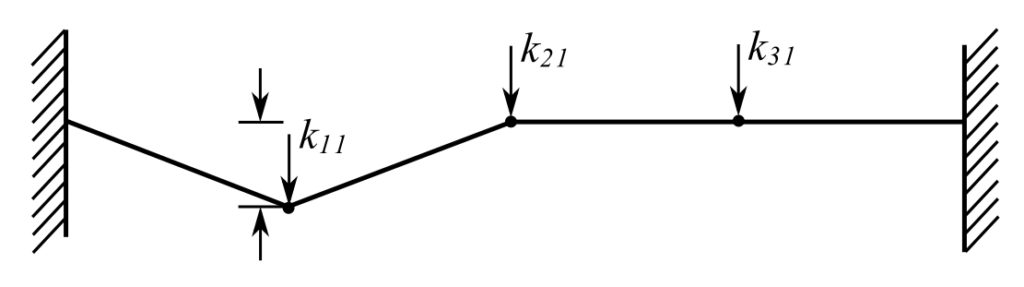
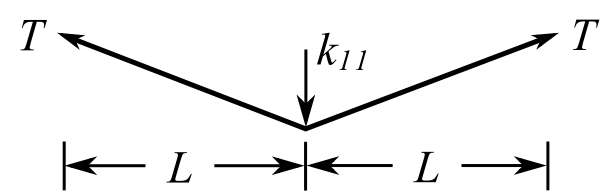
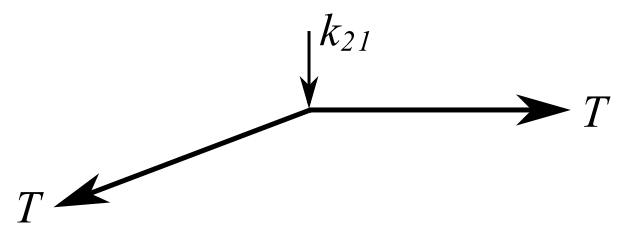
Therefore:

    \[k_{11} = \frac{2T}{L},\ k_{21} = \frac{-T}{L},\ k_{31} = 0 \]

    \[k_{22} = \frac{2T}{L},\ k_{12} = k_{32} = \frac{-T}{L} \]

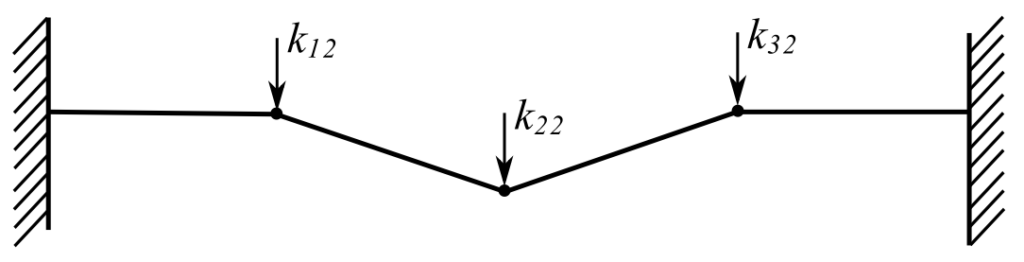
Therefore:

    \[ \frac{T}{L} \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{bmatrix} = [k] \]

Flexibilty

    \[ T\Big[\frac{a_{11}}{L} + \frac{a_{11}}{3L}\Big] = 1 \]

    \[ T\Big[\frac{4a_{11}}{3L}\Big] = 1\]

    \[a_{11} = \frac{3L}{4T} = a_{33}\]

    \[a_{21} = \frac{2}{3}a_{11} = \frac{L}{2T} \]

    \[a_{31} = \frac{1}{3}a_{11} = \frac{L}{4T} \]

    \[1 = 2T\frac{a_{22}}{2L}\]

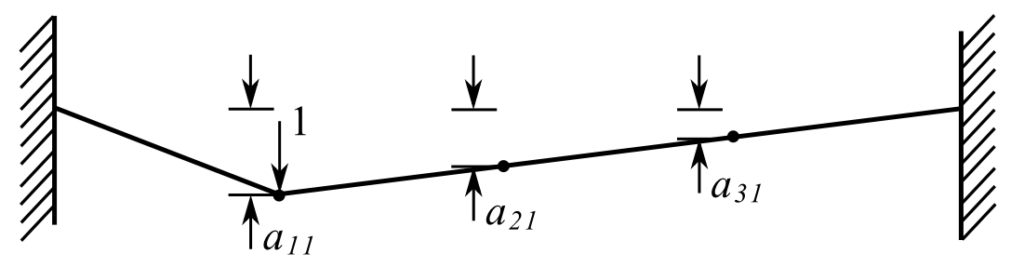
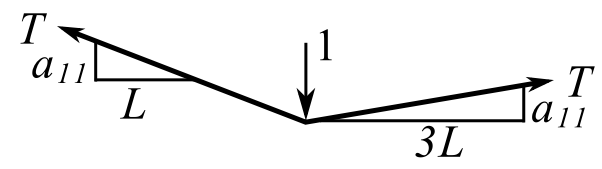
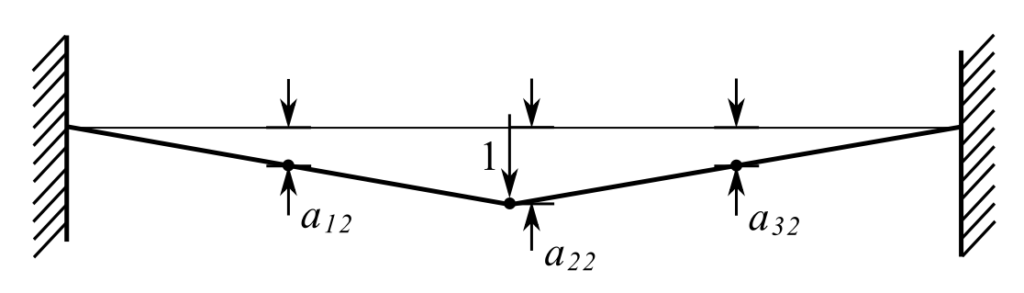
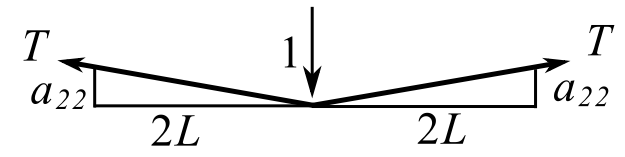
Therefore:

    \[1 = T\frac{a_{22}}{L}\]

    \[a_{22} = \frac{L}{T}\]

    \[a_{12} = \frac{L}{2T} = a_{32}\]

Thus:

    \[\frac{L}{T}\begin{bmatrix} \frac{3}{4} & \frac{1}{2} & \frac{1}{4} \\[2ex] \frac{1}{2} & 1 & \frac{1}{2} \\[2ex] \frac{1}{4} & \frac{1}{2} & \frac{3}{4} \end{bmatrix} = [a_{ij}] \]

Therefore:

    \[ \begin{split} [a][k] &= \begin{bmatrix} \frac{3}{4} & \frac{1}{2} & \frac{1}{4} \\[2ex] \frac{1}{2} & 1 & \frac{1}{2} \\[2ex] \frac{1}{4} & \frac{1}{2} & \frac{3}{4} \end{bmatrix} \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{bmatrix} \\&= \begin{bmatrix} \frac{3}{2} - \frac{1}{2} & -\frac{3}{4} + 1 -\frac{1}{4} & -\frac{1}{2} + \frac{1}{2} \\[2ex] 1-1 & -\frac{1}{2} + 2 - \frac{1}{2} & -1+1 \\[2ex] \frac{1}{2} - \frac{1}{2} & -\frac{1}{4} + 1 - \frac{3}{4} & -\frac{1}{2} + \frac{3}{2} \end{bmatrix} \\&= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

As an example of MDOF, consider a general planar situation which can be specialized to different industrial situations. Many of these problems can be initially modelled as SDOF ones, and then MDOF analysis will allow interpretations of the simplifying assumptions made.

NOTE: While the body shown is a rectangular shape, it can be any rigid body with a mass m and moment of inertia J_o about an axis \perp to the plane through the center of gravity. The horizontal stiffness components, designated by \ell_i are most often just the lateral stiffness of the vertically mounted spring. For real springs, the lateral spring stiffness may be hard to find in the literature. For coil springs, it is often in the range of 0.8-1.2 times the longitudinal value.

    \[\begin{split} +\rightarrow \sum F_x &= m\ddot{x} \\&= -\ell_1(x + h\theta) - \ell_2(x+h\theta) \quad (1) \end{split} \]

    \[\begin{split} +\uparrow \sum F_y &= m\ddot{y} \\&= -k_1(y-a\theta) - k_2(y + b\theta) \quad (2) \end{split} \]

    \[+\circlearrowleft \sum M_G = J_G\ddot{\theta} = -\ell_1(x+h\theta)h - \ell_2(x+h\theta)h + k_1(y-a\theta)a - k_2(y + b\theta)b \quad (3) \]

    \[m\ddot{x} + \ell_1x + \ell_1h\theta + \ell_2x + \ell_2h\theta = 0 \quad (1)\]

    \[m\ddot{y} + k_1y - k_1a\theta + k_2y + k_2b\theta = 0 \quad (2) \]

    \[J_G\ddot{\theta} + \ell_1xh + \ell_1h^2\theta + \ell_2xh + \ell_2h^2\theta - k_1ay + k_1a^2\theta + k_2by + k_2b^2\theta = 0 \quad (3) \]

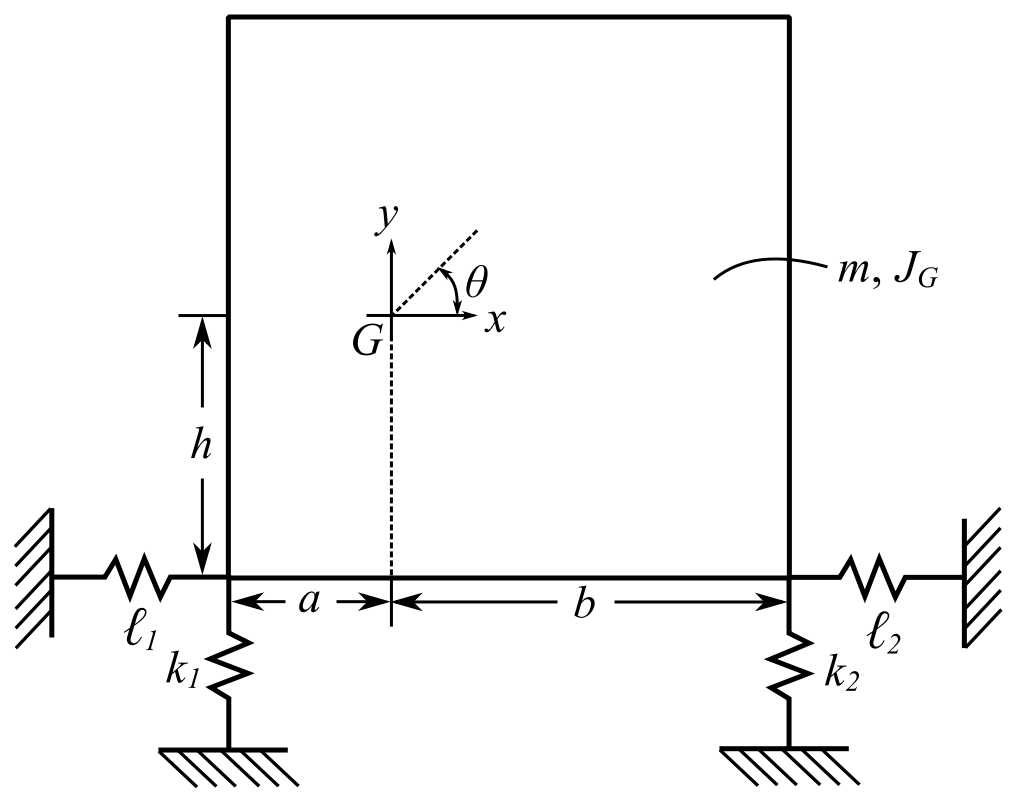
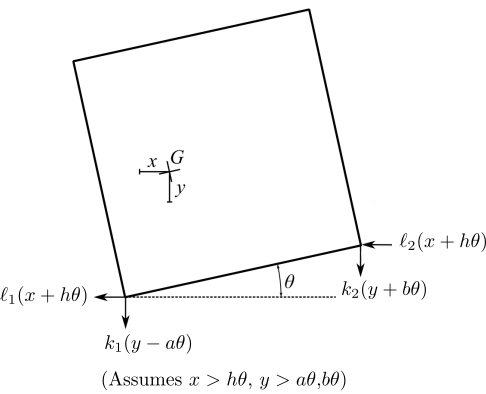
In matrix form:

    \[ \begin{Bmatrix} 0 \\ 0 \\ 0 \end{Bmatrix} = \begin{bmatrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & J_G \end{bmatrix} \begin{Bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{\theta} \end{Bmatrix} + \begin{bmatrix} \ell_1 + \ell_2 & 0 & (\ell_1+\ell_2)h \\ 0 & k_1 + k_2 & k_2b - k_1a \\ (\ell_1+\ell_2)h & k_2b-k_1a & h^2(\ell_1+\ell_2) + k_1a^2 +k_2b^2 \end{bmatrix} \begin{Bmatrix} x \\ y \\ z \end{Bmatrix} \]

Now find the stiffness matrix using influence coefficients.

First consider a unit displacement in the x direction only:

    \[\begin{split} + \rightarrow\sum F_x &= 0 \\& = k_{11} - (\ell_1 + \ell_2) \\ \implies k_{11} &= \ell_1 + \ell_2\end{split}\]

    \[\begin{split} + \uparrow\sum F_y &= 0 \\ \implies k_{12} &= 0 \end{split}\]

    \[\begin{split} +\circlearrowleft\sum M_G &= 0 \\& = k_{13} - (\ell_1+\ell_2)h\\ \implies k_{13} &=(\ell_1 + \ell_2)h \end{split} \]

For the y direction unit displacement:

    \[ \begin{split} +\uparrow\sum F_y & = 0 \\& = k_{22} - (k_1 + k_2) \end{split} \]

    \[\implies k_{22} = k_1 + k_2 \]

    \[\begin{split} + \circlearrowleft \sum M_G &= 0 \\& = k_{23} + k_1a - k_2b \end{split}\]

    \[\implies k_{23} = k_2b-k_1a\]

    \[+\rightarrow \sum F_x = 0\]

    \[\implies k_{21} = 0\]

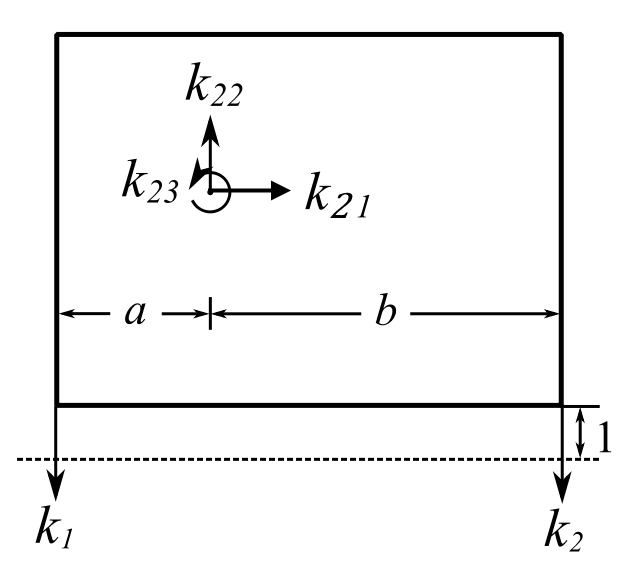
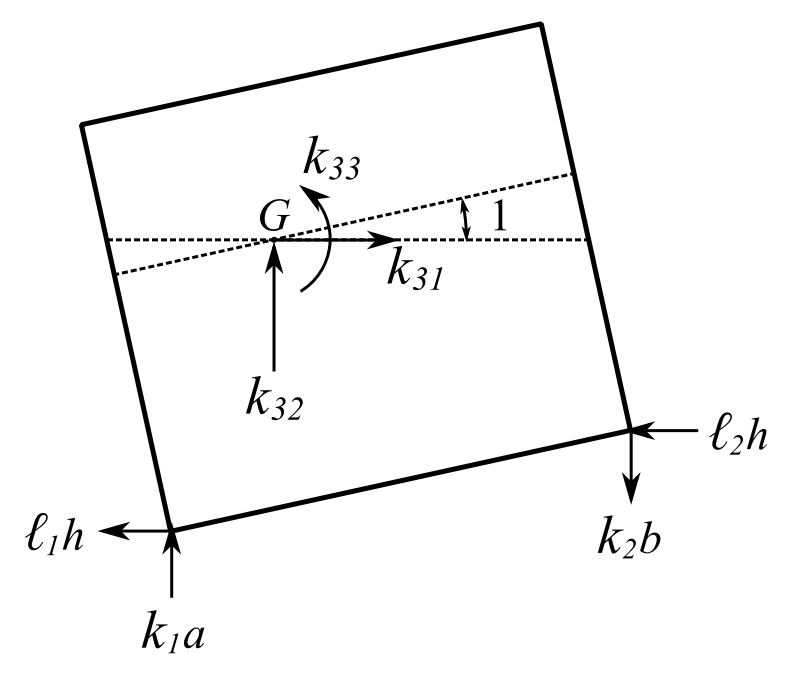
Assuming all summations for x direction, y direction and moment equal to 0:

    \[+\rightarrow \sum F_x = k_{31} - \ell_1h - \ell_2h = 0\]

    \[\implies k_{31} = (\ell_1 + \ell_2)h \]

    \[+\uparrow \sum F_y = k_{32} + k_1a-k_2b = 0\]

    \[ \implies k_{32} = k_2b - k_1a\]

    \[+\circlearrowleft \sum M_G = k_{33} -(\ell_1 + \ell_2)h^2 - k_1a^2 - k_2b^2 = 0\]

Therefore:

    \[k_{33} = (\ell_1+\ell_2)h^2 + k_1a^2 + k_2b^2\]

This yields the same stiffness matrix.

As long as we use the motions about the center of gravity then the inertia (mass) matrix is just the mass or the mass moment of inertia about the center of gravity. If we use coordinates to describe the motion that are not related to the absolute motion of the center of gravity then the stiffness matrix may not be symmetric and the mass matrix will not be diagonal.

Inertia Influence Coefficients

The elements of the mass matrix, m_ij can be determined through the use of inertia influence coefficients. They are defined as the set of impulses applied at the points (representing the coordinate directions) 1, 2, \ldots n respectively to produce a unit velocity at point j and zero velocity at every other point.

NOTE: If x_j denotes an angular coordinate then \dot{x}_j represents an angular velocity

Thus for a multi-degree of freedom system, the total impulses at points i is:

    \[\tilde{F}_i = \sum_{j = 1}^n m_{ij}\dot{x}_j\]

    \[\{\tilde{F}\} = [m]\{\dot{x}_i\}\]

    \[[m] = \begin{bmatrix} m_{11} & \ldots &m_{1n} \\ \vdots & & \vdots \\ m_{n1} & \ldots & m_{nn} \end{bmatrix}\]

    \[\tilde{F} = \begin{Bmatrix} F_1 \\ \vdots \\ F_n \end{Bmatrix} \]

    \[\{\dot{x}\} = \begin{Bmatrix} \dot{x}_1 \\ \vdots \\ \dot{x}_n \end{Bmatrix} \]

To find the m_{ij}

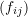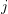  1. Assume that a set of impulses (f_{ij}) are applied at all points i = 1, 2, \ldots, n as to produce a unit velocity at point j only(with zero velocity in all the after directions (coordinates)). By definition the set of impulses 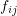f_{ij} denote the influence inertia coefficients m_{ij}
  2. Repeat the procedure for each point j = 1, 2, \ldots, n.
Example

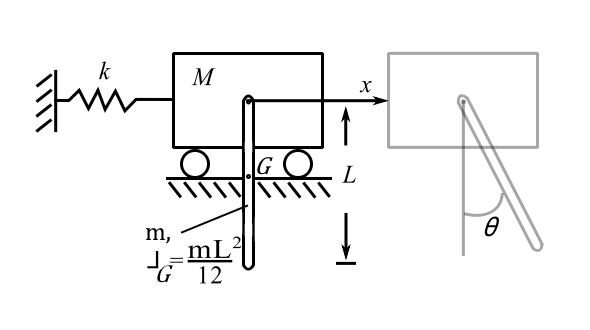
First apply unit velocity to x only:

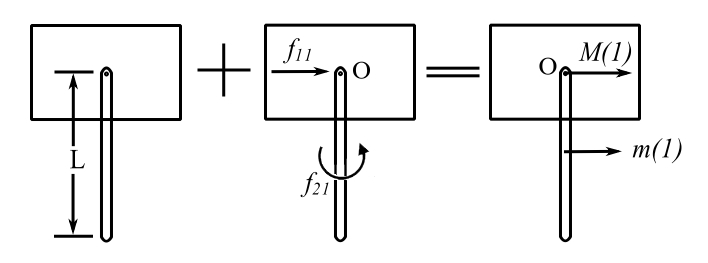
    \[ \begin{split} +\rightarrow \sum L &= f_{11} \\&= (M+m) \\&= m_{11} \end{split}\]

    \[\begin{split} +\circlearrowleft \sum H_0 &= f_{21} \\&= m\frac{L}{2} \\& = m_{21}\end{split}\]

Apply unit velocity(angular) to \theta only

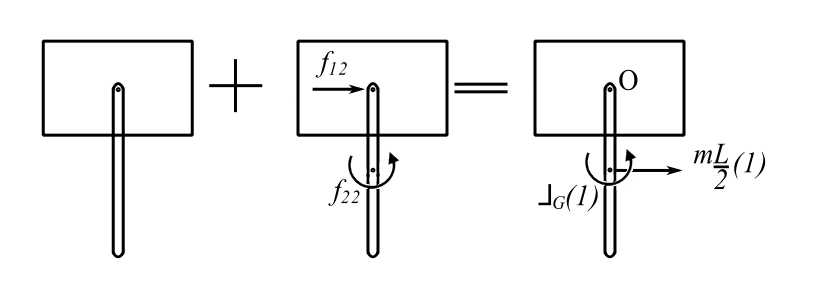
    \[\begin{split} +\rightarrow \sum L &= f_{12} \\&= \frac{mL}{2} \\&= m_{12}\end{split}\]

    \[ \begin{split} +\circlearrowleft \sum H_0 &= J_G(1) + \frac{mL}{2}(1)\frac{L}{2} \\&= \frac{1}{12}mL^2+\frac{mL^2}{4} \\&= \frac{mL^2}{3} \\&=m_{22}\end{split} \]

Therefore:

    \[\begin{bmatrix} M + m & \frac{mL}{2} \\ \frac{mL}{2} & \frac{mL^3}{3} \end{bmatrix}\]

Now find the stiffness matrix

Apply unit deflection to x only:

Therefore

    \[k_{11} = k\]

    \[k_{21} = 0\]

Apply unit deflection to \theta only:

    \[ \begin{split} +\circlearrowleft \sum M_0 &= k_{22} - mg\frac{\ell}{2}(1) \\&= 0\end{split}\]

    \[ k_{22} = mg\frac{\ell}{2}\]

    \[ k_{12} = 0\]

Therefore:

    \[\begin{bmatrix} M + m & \frac{mL}{2} \\ \frac{mL}{2} & \frac{mL^3}{3} \end{bmatrix} \begin{Bmatrix} \ddot{x} \\ \ddot{\theta} \end{Bmatrix} + \begin{bmatrix} k_1 & 0 \\0 & \frac{mgL}{2} \end{bmatrix}\begin{Bmatrix} x \\\theta \end{Bmatrix}= \begin{Bmatrix} 0 \\0 \end{Bmatrix}\]

Page Comments

  1. Olek says:
    April 10, 2024 at 7:59 am

    It is explained in great details and so clear, I have found such information on springs coefficients calculation nowerewhere. So greatful

    Reply

Leave a Reply

Your email address will not be published.