Advanced Dynamics and Vibrations: Modal analysis of mdof systems with generalized coordinates, semi-definite systems, repeated roots
Introduction to Normal Mode Analysis
Our analysis of MDOF systems has shown that regardless of the coordinates used that there are specific properties of the system(natural frequencies, mode shapes) that do not depend on our choices. These properties can be used to uncouple the equations of motion into ![]() equations that can be easily solved and then transformed back to the original coordinates which are the most useful form to use the results. The process uses the modal shapes, in the form of vectors, to build a modal matrix. Consider the modal vectors
equations that can be easily solved and then transformed back to the original coordinates which are the most useful form to use the results. The process uses the modal shapes, in the form of vectors, to build a modal matrix. Consider the modal vectors ![]() . The modal matrix is formed by making these vectors the columns in the matrix:
. The modal matrix is formed by making these vectors the columns in the matrix:
![]()
but instead of using ![]() we normalize it to
we normalize it to ![]() using the mass matrix so that:
using the mass matrix so that:
![]()
or
![]()
NOTE:
![]()
To start, consider the undamped forced 2DOF system:
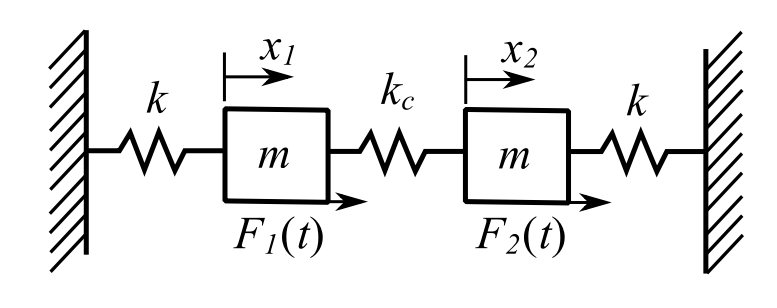
![]()
Therefore:
![]()
![]()
![]()
![]()
Normalize ![]() and
and ![]() using
using ![]() where
where ![]() . Therefore:
. Therefore:
![]()
![]()
![]()
![]()
Therefore:
![]()
![]()
NOTE Orthogonality:
![]()
![]()
Modal vectors are orthogonal with respect to ![]() or
or ![]() . Thefore the modal matrix is:
. Thefore the modal matrix is:
![]()
![]()
Now transform the equations of motion using ![]() by setting
by setting ![]() then
then ![]() .
.
![]()
![]()
Now multiply the equations of motion by ![]() to get:
to get:
![]()
Therefore, the transformed equations become
Where
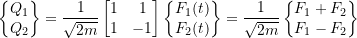
We can now solve this set of uncoupled SDOF equations for the free, transient on steady-state conditions. In the transformed state the stiffness matrix is now the matrix of natural frequencies:
After solving we transform back to the original condition.
Normal analysis of MDOF systems
The equations of motion for viscously damped MDOF systems are in general
![]()
For up to 2 DOF we can easily use a complex analysis (transform methods). However for larger system we often use modal analysis.
In this approach we start with the homogeneous equations and we will also start with the undamped case. (We will return to it later!) Therefore,
![]()
We look for so-called synchronous motions SSHM (Simultaneous Simple Harmonic motion) by assuming
![]()
or
![]()
and get
![]()
This is true for only special ![]() say
say ![]() and special
and special ![]() associated with
associated with ![]()
We can find the ![]() & the
& the ![]() within a multiplicative constant. Each
within a multiplicative constant. Each ![]() and its associated
and its associated ![]() is called a mode.
is called a mode.
If the ![]() are distinct then we can easily show that the
are distinct then we can easily show that the ![]() are orthogonal to one another in some sense. To see this consider the two modes say
are orthogonal to one another in some sense. To see this consider the two modes say ![]() &
& ![]() , then
, then
![]()
![]()
Multiply the first by ![]()
![]()
and the second by ![]()
![]()
Since we can transpose the first equation so that the left hand side are the same. It suggests that
![]()
Therefore, the modal vector ![]() are orthogonal with respect to the mass and stiffness matrices.
are orthogonal with respect to the mass and stiffness matrices.
These eigenvectors form a linearly independent set i.e. any motion of the system can be thought of as a linear combination of these modes. Physically this implies that any motion can be thought of as a superposition of these normal modes.
Linear independence means that we cannot write any vector as a combination of the others. If they were linearly dependent there should be some way to combine them to produce one from the others. This means there should be:
![]()
But if we premultiply this equation by ![]() we get:
we get:
![]()
but all the terms are zero (orthogonality) except for ![]() and therefore
and therefore ![]() . The same is true for each term therefore
. The same is true for each term therefore ![]()
As a result any motion can be written as a linear combination of the modal vectors. They are a set of basis vectors in the same way as ![]() are for
are for ![]() positions. Therefore,
positions. Therefore,
![]()
Where ![]() is the modal participation factor and
is the modal participation factor and
![]()
This is called the expansion theorem in vibration where the ![]() are functions of time.
are functions of time.
It turns out that if we have repeated eigenvalue we can still find a set of eigenvectors that span the system.
We can use these properties of the system to solve these equations in general. The process uses the modal vectors put together in a so-called modal matrix. Before starting we will normalize the modal vectors ![]() into
into ![]() as they are only known to within a multiplicative constant.
as they are only known to within a multiplicative constant.
The normalization is:
![]()
Therefore,
![]()
Now form the modal matrix
![]()
Then
![]()
Therefore
![]()
Now to solve the original system we transform the equations to a set of generalized coordinates. That is we set:
![]()
![]()
putting this into the original set of equation gives:
![]()
now premultiply by ![]()
![]()
This uncouples the equations so that each looks like:
![]()
The general solution of this equation is:
![]()
We can then transform the solution back to the original coordinates using:
![Rendered by QuickLaTeX.com \[\begin{split} \{x(t)\} &= [\mu] \{\eta (t)\} \\&= \sum_{r=1}^{n} \{\mu\}_{r} \eta _{r} (t) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-18fee1cfe8593a42fb464817009eee39_l3.png)
This expression contains the initial conditions in the transformed coordinates and are related to the original values by:
![]()
![]()
We can also solve the steady-state forced problem by simply considering the particular integral instead of the total solution.
Summary (Free Vibration)
We have been considering the solution of
![]()
Where we transform the equation using
![]()
If we premultiply by ![]() and substitute into
and substitute into ![]() we get:
we get:
![]()
but
![]()
![]()
Therefore
![]()
The solution to these equation ![]() is
is
![]()
Where ![]() &
& ![]() are constants, therefore
are constants, therefore
![Rendered by QuickLaTeX.com \[\begin{split} \{x(t)\} &= [\mu] \{\eta (t)\} \\&= \sum_{r=1}^{n} \eta _{r} (t) \{\mu\}_{r} \\&= \sum_{r=1}^{n} C_{r} \{\mu\}_{r} \cos (p_{r} t - \phi _{r})\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ac1ef5117cc79a0a8153866d2327d92e_l3.png)
If ![]() and
and ![]() are the initial displacements and velocities then
are the initial displacements and velocities then
![]()
![]()
Therefore,
![]()
![]()
since ![]() , therefore
, therefore
![]()
This solves every free vibration problem for any initial conditions.
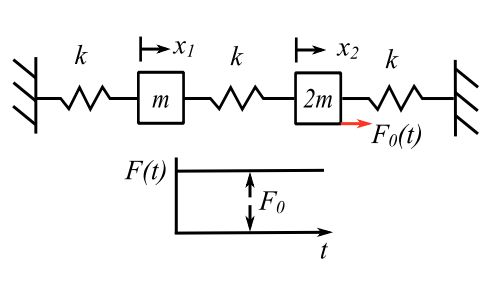
![Rendered by QuickLaTeX.com \begin{equation*} [m] = \begin{bmatrix} m & 0 \\ 0 & 2m \\ \end{bmatrix} \end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e0ab99a2c898715f597ac02edf71cba7_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} [k] = k \begin{bmatrix} 2 & -1 \\ -1 & 2 \\ \end{bmatrix} \end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ca6010155440f4742aa962c210ef03a9_l3.png)
Therefore
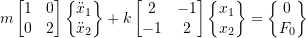
Characteristic equation is:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} p^2 &= \bigg[ \frac{3}{2} \pm \sqrt{\frac{9}{4} - \frac{3}{2}} \bigg] \frac{k}{m} \\&= \bigg( \frac{3}{2} \pm \frac{\sqrt{3}}{2} \bigg)\frac{k}{m} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-dc2e032353a6d25cbc4402a87c1c9999_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} p_{1}^{2} &= \bigg( \frac{3-\sqrt{3}}{2} \bigg) \frac{k}{m} \\&= 0.634 \frac{k}{m} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f02490386e676dbaa4458f12f0904119_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\begin{split} p_{2}^{2} &= \bigg( \frac{3+\sqrt{3}}{2} \bigg)\frac{k}{m} \\&= 2.366 \frac{k}{m} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-76afc475d96524724a9d000114876b1f_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\begin{split} \bigg( \frac{u_{2}}{u_{1}} \bigg)_{1} &= 2 - \frac{mp_{1}^{2}}{m} \\&= 2- 0.634 \\&= 1.366 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-79b68b2ef9f6dbcd63b81d8229aef782_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} \bigg( \frac{u_{2}}{u_{1}} \bigg)_{2} &= 2 - \frac{mp_{2}^{2}}{m} \\&= 2- 2.366 \\&= -0.366 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-20ab4fdff0bbba5e2e55922fae413c41_l3.png)
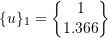
![]()
Therefore,
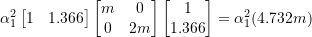
Therefore,
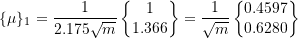
Similarly:
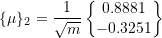
now find the force vector in the normal coordinates
![Rendered by QuickLaTeX.com \begin{equation*} \{N(t)\} = [u]^{T} \begin{Bmatrix} 0 \\ F_o \\ \end{Bmatrix} = \frac{1}{\sqrt{m}} \begin{bmatrix} 0.4597 & 0.6280\\ 0.8881 & -0.3251\\ \end{bmatrix} \begin{Bmatrix} 0 \\ F_o \\ \end{Bmatrix} = \frac{F_o}{\sqrt{m}} \begin{Bmatrix} 0.6280 \\ -0.3251 \\ \end{Bmatrix} \end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-096501d47715852fe5694c94e1c692ec_l3.png)
Since there are initial conditions with no displacement and no velocity we can simply integrate the convolution integrals to give
![Rendered by QuickLaTeX.com \[\begin{split} \eta_{1}(t) &= \frac{0.6280 F_{o}}{p_1 \sqrt{m}} \int_{0}^{t} \sin p(t-\tau ) \,d \tau \\&= \frac{0.6280 F_{o}}{p_{1}^{2} \sqrt{m}}(1- \cos p_{1} t) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ec2415f4a030160e0bf78d0e750fa0e4_l3.png)
![]()
We can now find the response in terms of the original coordinates using:
![]()
![Rendered by QuickLaTeX.com \[\begin{split} x_{1}(t) &= \frac{(0.4597)(0.6280)F_{o}}{p_{1}^{2} m} \bigg(1 - \cos p_1 t \bigg) + \frac{(0.8881)(-0.3251)F_{o}}{p_{2}^{2} m} \bigg(1 - \cos p_2 t \bigg) \\&= \frac{F_o}{k} \frac{(0.4597)(0.6280)}{(0.634)} \bigg(1- \cos(0.796) \sqrt{\frac{k}{m}} t \bigg) + \frac{F_o}{k} \frac{(0.8881)(-0.3251)}{(2.366)} \bigg(1- \cos(1.5382) \sqrt{\frac{k}{m}} t \bigg) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fae9e285d8731592631f54a99ed0a96b_l3.png)
![]()
![]()
Note that the first mode is most pronounced in the overall response.
Check static deflection:
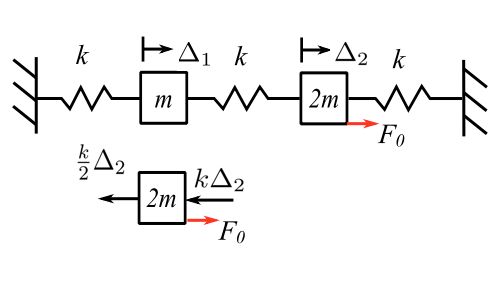
Therefore, ![]() ,
, ![]()
![Rendered by QuickLaTeX.com \[\begin{split} x_2 \text{(static)} &= \frac{F_o}{k} (0.6219 + 0.0447) \\&= \Delta _2 \\&= \frac{F}{k} (0.6666) \qquad \text{O.K.} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c6d883562d1644538e48bb9586ee2ca8_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} x_1 \text{(static)} &= \Delta _1 \\&= \frac{\Delta _2}{2} \\&= \frac{F_o}{k} (0.4553 - 0.1220) \\&= \frac{F_{o}}{3k} \\&= 0.3333\frac{F_{o}}{k} \qquad \text{O.K.} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-30bf208e2aae8963771fdae516bed7a6_l3.png)
Consider a second example with certain initial conditions:
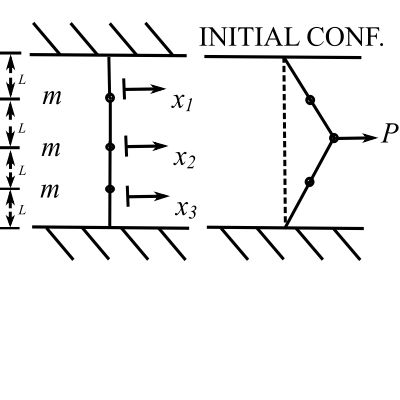
A static force ![]() is suddenly released for the system of 3 masses mounted on a tightly stretched wire with tension
is suddenly released for the system of 3 masses mounted on a tightly stretched wire with tension ![]() . Determine the resulting free vibration using normal mode analysis.
. Determine the resulting free vibration using normal mode analysis.
Solution:
While the mass matrix is easy we must find the stiffness matrix using say ![]()
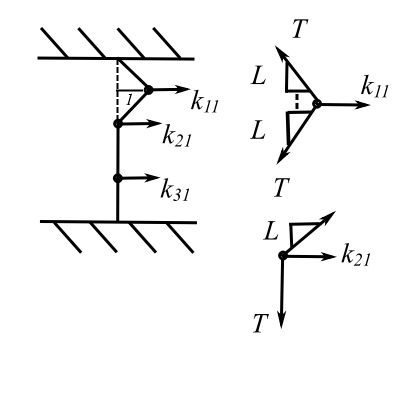
Apply unit deflection to ![]() ,
,
![Rendered by QuickLaTeX.com \[\begin{split} \sum F_{x} &= 0 \\&= k_{11} - T \left(\frac{1}{L}\right) - T \left(\frac{1}{L}\right) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-eb6a3b78c23a52503441fcecb8184cb5_l3.png)
Therefore,
![]()
![]()
![]()
Therefore,
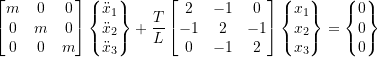
now find the ![]() ‘s &
‘s & ![]() , assume
, assume ![]() to get:
to get:

where
![]()
The characteristic equation is ![]()
![]()
![]() or
or ![]()
Therefore,
![]()
![]()
now find ![]() , choose
, choose ![]()
![]()
![]()
![]()
For ![]()
For ![]()
For ![]()
Therefore,
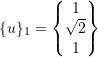
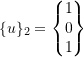
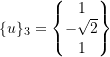
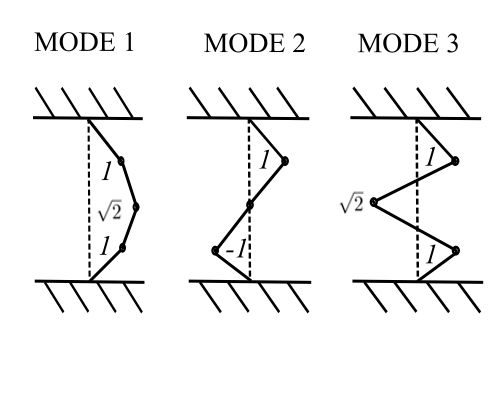
now normalize the ![]() to get
to get ![]() where
where ![]() , therefore as
, therefore as ![]()
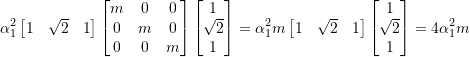
![]()
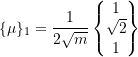
Similarly,
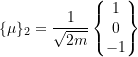
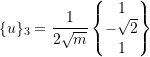
Therefore,

Also need the initial conditions
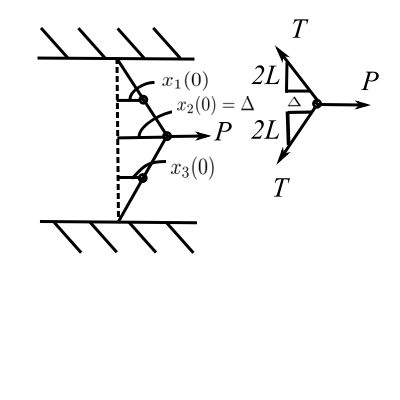
Therefore
![]()
![]()
![]()
![]()
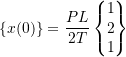
![]()
We can simply put this into the general solution:
![]()

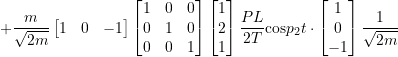
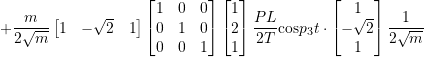
![]()
![]()
![]()
Again the first mode is the dominant one and the second unsymmetric mode is not present. If we had chosen different initial condition, then

![Rendered by QuickLaTeX.com \[\begin{split} p &= \frac{\Delta}{L}T + \frac{\Delta}{3L} T \\&= \frac{4}{3} \frac{\Delta T}{L} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-560aa211ddf662ab8fbae37033420df1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} \Delta &= \frac{3}{4} \frac{PL}{T} \\&= x_{1}(0) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8260aab6ad33f422e67bc538ee2bef55_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} x_{2}(0) &= \left(\frac{2}{3}\right) \left(\frac{3}{4}\right) \frac{PL}{T} \\&= \frac{PL}{2T} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0ca335c84653a1b80fe36b1ce590c995_l3.png)
![]()
Therefore
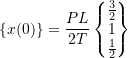
All three modes would now participate in the motion. To find the response simply insert the new ![]() and calculate the
and calculate the ![]() .
.
e.g Steady State
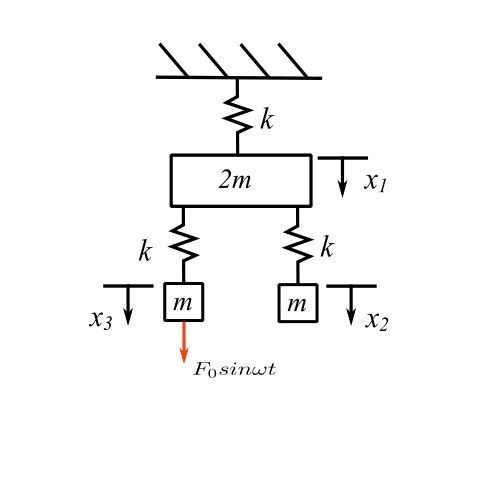
The equations of motion are
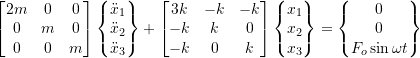
Therefore,
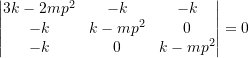
![]()
Divide by ![]() and set
and set ![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
Note: ![]() ,
,
![]()
![]()
![]()
For ![]()
Therefore, from ![]() and
and ![]()
![]()
From ![]() ,
,
![]()
![Rendered by QuickLaTeX.com \[\begin{split} A_{1} &= \frac{2}{3 - \frac{5-\sqrt{17}}{2}} \\&= 0.78078 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-75f84c11aca7aa560f5c76256bdafa78_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}A\end{Bmatrix}^1 =\begin{pmatrix}0.78078 \\ 1 \\ 1\end{pmatrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3e95945ba328166380f8a4049bea9e8f_l3.png)
For ![]()
![]() therefore
therefore ![]()
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}A\end{Bmatrix}^2 =\begin{pmatrix}0 \\ 1 \\ -1\end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-023c3afa60c45a47e121d669c458a8b9_l3.png)
For ![]()
Again ![]()
![Rendered by QuickLaTeX.com \[ \begin{split}A_1 &= \left(1 - \frac{5+\sqrt{17}}{4}\right)A_2 \\A_1 &= -1.28078\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9510e1a5ade6853f27ced1be399cbc4c_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}A\end{Bmatrix}^3 =\begin{Bmatrix}-1.28078 \\ 1 \\ 1\end{Bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b36f6712154aef57d3bcece2cff86cba_l3.png)
Normalized eigenvectors
![Rendered by QuickLaTeX.com \[ \begin{split} \alpha_1^2\begin{Bmatrix}A\end{Bmatrix}^T_1\begin{bmatrix}m\end{bmatrix}\begin{Bmatrix}A\end{Bmatrix}_1&= 1 \\ \alpha_1 &= \frac{0.55734}{\sqrt{m}} \\ \alpha_2^2\begin{Bmatrix}A\end{Bmatrix}^T_2\begin{bmatrix}m\end{bmatrix}\begin{Bmatrix}A\end{Bmatrix}_2&= 1 \\ \alpha_2 &= \frac{1}{\sqrt{2m}} = \frac{0.70711}{\sqrt{m}} \\ \alpha_3^2\begin{Bmatrix}A\end{Bmatrix}^T_3\begin{bmatrix}m\end{bmatrix}\begin{Bmatrix}A\end{Bmatrix}_3&= 1 \\ \alpha_3 &= \frac{0.43516}{\sqrt{m}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a9e753116afbcc949c0e533bba054aa9_l3.png)
therefore:
![Rendered by QuickLaTeX.com \[\begin{bmatrix}u\end{bmatrix} = \frac{1}{\sqrt{m}}\begin{bmatrix}0.43516 && 0 && -0.55734 \\0.55734 && 0.70711 && 0.43516 \\0.55734 && -0.70711 && 0.43516\end{bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-681702ad6b95f13f9fcb48f81b4e9337_l3.png)
The transformed forces are:
![Rendered by QuickLaTeX.com \[\begin{bmatrix}u\end{bmatrix}^T\begin{Bmatrix}0 \\ 0 \\ F_0\end{Bmatrix} \sin\omega t= \frac{F_0}{\sqrt{m}}\begin{Bmatrix}0.55734 \\ -0.70711 \\ 0.43516\end{Bmatrix}\sin \omega t\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bd631c62bc852bc2b1e6a320b27d6c31_l3.png)
Therefore transformed equations are:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}\Ddot{\eta}\end{Bmatrix} +\begin{bmatrix}p^2\end{bmatrix}\eta =\frac{F_0}{\sqrt{m}}\begin{Bmatrix}0.55734 \\ -0.70711 \\ 0.43516\end{Bmatrix} \sin\omega t\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b9bb9be93915c6c9d772fab43e50a47d_l3.png)
Steady State Solutions of these equations
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix}x\end{Bmatrix} &= \begin{bmatrix}u\end{bmatrix}\begin{Bmatrix}\eta\end{Bmatrix} \\&= \frac{F_0}{k}\begin{bmatrix}0.43516 && 0 && -0.55734 \\0.55734 && 0.70711 && 0.43516 \\0.55734 && -0.70711 && 0.43516\end{bmatrix}\begin{Bmatrix}\frac{0.55734}{(1-\frac{\omega^2}{P_1^2})} \\\frac{-0.70711}{(1-\frac{\omega^2}{P_2^2})} \\\frac{0.43516}{(1-\frac{\omega^2}{P_3^2})}\end{Bmatrix}\sin\omega t\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d18ef44b8249038f38ceee5a8493edc0_l3.png)
For the case in which we have repeated eigenvalues we can still have orthogonal eigenvectors using a process called successive orthogonalization.
If the eigenvalues is repeated ![]() times let
times let ![]() be an arbitrary set of modal vectors that satisfy the degenerate set of equations. We construct an orthoganal set using
be an arbitrary set of modal vectors that satisfy the degenerate set of equations. We construct an orthoganal set using
![]()
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix}u\end{Bmatrix}_2 = \begin{Bmatrix}u\end{Bmatrix}_{p_2} - \frac{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_{p_2}}{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_1} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4c0f025ecae4e2ad28143ae8155f6b4f_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix}u\end{Bmatrix}_3 = \begin{Bmatrix}u\end{Bmatrix}_{p_3} - \frac{\begin{Bmatrix}u\end{Bmatrix}^T_2 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_{p_3}}{\begin{Bmatrix}u\end{Bmatrix}^T_2 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_2} \begin{Bmatrix}u\end{Bmatrix}_2 - \frac{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_{p_3}}{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_1} \begin{Bmatrix}u\end{Bmatrix}_1 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5ef7f2e8ef3663d37d3a36b06b8b2c80_l3.png)
etc.
To prove take
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_2 = \begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_{p_2} -\frac{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_{p_2}}{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_1} \begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_1 = \underline{\underline{0}}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f898af77b0b9b27fa25f5351bd244c99_l3.png)
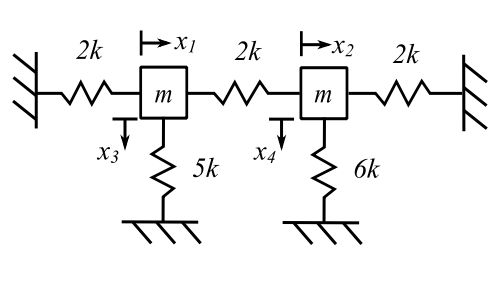
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}m\end{bmatrix} = m \begin{bmatrix}1 && 0 && 0 && 0 \\0 && 1 && 0 && 0 \\0 && 0 && 1 && 0 \\0 && 0 && 0 && 1\end{bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4a7e3274d4c10acecf2846318ea0862e_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}k\end{bmatrix} = k \begin{bmatrix}4 && -2 && 0 && 0 \\-2 && 4 && 0 && 0 \\0 && 0 && 5 && 0 \\0 && 0 && 0 && 6\end{bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8058b51477c21fc95c44cc8f638acc23_l3.png)
The characteristic equation is
![]()
![]()
Therefore
![Rendered by QuickLaTeX.com \[ \begin{vmatrix}4-\lambda && -2 && 0 && 0 \\-2 && 4-\lambda && 0 && 0 \\0 && 0 && 5-\lambda && 0 \\0 && 0 && 0 && 6-\lambda\end{vmatrix} = 0 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7af809d3ec8740523d30a3190593c905_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}&= (6-\lambda)\biggr[(4-\lambda)^2(5-\lambda)-4(5-\lambda)\biggr] \\&= (6-\lambda)(5-\lambda)(12-8\lambda+\lambda^2) \\&= (6-\lambda)(5-\lambda)(6-\lambda)(2-\lambda)\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cfbe6529faaa398dc4748c398dfb6adf_l3.png)
Therefore: ![]()
For the repeated root ![]()
![Rendered by QuickLaTeX.com \[ \begin{split}-2u_1-2u_2 &=0 \\-2u_1-2u_2 &= 0 \\u_3 &= 0 \\u_4 &= ?\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b7395aa546c9b1e9faf4aef1adb5ed27_l3.png)
from
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}4-\lambda && -2 && 0 && 0 \\-2 && 4-\lambda && 0 && 0 \\0 && 0 && 5-\lambda && 0 \\0 && 0 && 0 && 6-\lambda\end{bmatrix} \begin{Bmatrix}u_1 \\ u_2 \\ u_3 \\ u_4\end{Bmatrix} = \begin{Bmatrix}0 \\ 0 \\ 0 \\ 0\end{Bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d8a5a54f06c64edccc4cfbb7b61b3f1e_l3.png)
Therefore there are an infinite number of solutions so choose one which satisfies the equations. e.g.:
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix}u\end{Bmatrix}_1^{\ast} =\begin{bmatrix} 1 \\ -1 \\ 0 \\ 2 \end{bmatrix} =\begin{Bmatrix}u\end{Bmatrix}_1 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cd10cd4ddca18e9a32ed9db591864677_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix}u\end{Bmatrix}_2^{\ast} =\begin{Bmatrix} 2 \\ -2 \\ 0 \\ 0\end{Bmatrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7f1f6bc2688dfb709fb4bae555a18956_l3.png)
Now we make them orthogonal
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix}u\end{Bmatrix}_2 &= \begin{Bmatrix}u\end{Bmatrix}_2^{\ast} -\frac{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_2^{\ast}}{\begin{Bmatrix}u\end{Bmatrix}^T_1 \begin{bmatrix}m\end{bmatrix} \begin{Bmatrix}u\end{Bmatrix}_1} \begin{Bmatrix}u\end{Bmatrix}_1 \\&= \begin{Bmatrix}2 \\ -2 \\ 0 \\ 0\end{Bmatrix}-\frac{1}{6}\begin{bmatrix}1 && -1 && 0 && 2\end{bmatrix}\begin{bmatrix}2 \\ -2 \\ 0 \\ 0\end{bmatrix}\begin{Bmatrix}u\end{Bmatrix}_1 \\&= \frac{4}{3}\begin{Bmatrix}1 \\ -1 \\ 0 \\ -1\end{Bmatrix}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bdbae36d03e17dc0e179e2416b978af1_l3.png)
Now ![]() and
and  are orthonormal. For
are orthonormal. For ![]() therefore:
therefore:
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix}u\end{Bmatrix}_3 = \begin{bmatrix}1 \\ 1 \\ 0 \\ 0\end{bmatrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-530a129b5a9eff18d277da71d999f3f6_l3.png)
For ![]()
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}u\end{Bmatrix}_4=\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0\end{bmatrix} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9b897268166a4c9483b401e8a6955ff2_l3.png)
and this is our basis.
Proportional Damping
Now consider the addition of damping to the system
![]()
Now transform this to normal coordinates
![]()
and premultiply by ![]()
![]()
therefore:
![]()
but there is no a priori reason that ![]() is a diagonal matrix and therefore the equations are coupled. If it was, we could use the same approach as before. One condition that is often used is the so-called proportional damping where
is a diagonal matrix and therefore the equations are coupled. If it was, we could use the same approach as before. One condition that is often used is the so-called proportional damping where
![]()
so that the transformed equations are necessarily diagonal. We can then set
![]()
then each transformed equation is
![]()
The general solution of this equation is
![Rendered by QuickLaTeX.com \[ \begin{split}\eta_r(t) &= \frac{1}{\sqrt{1-\nu^2_r}p_r} \int_0^tN_r(t)e^{-\nu_r p_r(t-\tau)} \sin{\sqrt{1-\nu_r^2}} p_r(t-\tau)d\tau \\ &+ e^{-\nu_r p_r t} \biggr[\frac{\eta_r(0)}{\sqrt{1-\nu^2_r}}\cos(\sqrt{1-\nu_r^2}p_rt-\Psi_r) + \frac{\dot\eta(0)}{\sqrt{1-\nu^2_r}p_r} \sin\sqrt{1-\nu_r^2}p_r t \biggr]\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-81ca36755361084b9768be90cb267e89_l3.png)
where ![]()
Now consider that the ![]() are related
are related
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix}\mu\end{bmatrix}^T\begin{bmatrix}c\end{bmatrix}\begin{bmatrix}\mu\end{bmatrix} &=\alpha \begin{bmatrix}\mu\end{bmatrix}^T\begin{bmatrix}m\end{bmatrix}\begin{bmatrix}\mu\end{bmatrix} +\beta \begin{bmatrix}\mu\end{bmatrix}^T\begin{bmatrix}k\end{bmatrix}\begin{bmatrix}\mu\end{bmatrix} \\&= \alpha \begin{bmatrix}I\end{bmatrix} +\beta \begin{bmatrix}p^2\end{bmatrix} \\ &:=\begin{bmatrix} 2\nu p \end{bmatrix}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-97abaa9c8a1d21020c524452af93fe47_l3.png)
therefore
![Rendered by QuickLaTeX.com \[ \begin{split}\alpha +\beta p_i^2 &= 2\nu_i p_i \\\nu_i &= \frac{1}{2p_i}(\alpha+\beta p_i^2) \\ &=\frac{\alpha}{2p_i} + \frac{\beta p_i}{2}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fd0fcc188dae1a443669f8859cb6e872_l3.png)
Therefore we can only choose the damping independently for 2 modes. If ![]() then
then ![]() so that the damping in each mode is proportional to the frequency of that mode. The higher the frequency the higher the damping so that higher modes damp out more rapidly. [Note: Often called relative damping.]
so that the damping in each mode is proportional to the frequency of that mode. The higher the frequency the higher the damping so that higher modes damp out more rapidly. [Note: Often called relative damping.]
On the other hand, setting ![]() implies the damping is proportional to the mass matrix
implies the damping is proportional to the mass matrix ![]() which damps out the lower modes more than the higher ones. [Note: Often called absolute damping.]
which damps out the lower modes more than the higher ones. [Note: Often called absolute damping.]
Return to a simple problem we have done previously

![]()
![Rendered by QuickLaTeX.com \[ \begin{split}p_1 &= \sqrt{\frac{k}{m}} \\\begin{pmatrix}X_2 \\ X_1 \end{pmatrix}_1 &= \begin{Bmatrix} 1 \\ 1\end{Bmatrix} \\p_2 &= \sqrt{\frac{k+2k_c}{m}} \\\begin{pmatrix}X_2 \\ X_1 \end{pmatrix}_2 &= \begin{Bmatrix} 1 \\ -1\end{Bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-19caa2e49c49e29a66fc881c971bfc40_l3.png)
Normalize
![Rendered by QuickLaTeX.com \[ \begin{split}m\alpha_1^2 \begin{bmatrix}1 && 1\end{bmatrix}\begin{bmatrix}1 && 0 \\ 0 && 1\end{bmatrix}\begin{bmatrix} 1 \\ 1\end{bmatrix} &=\alpha_1^2m \begin{bmatrix}1 && 1\end{bmatrix}\begin{bmatrix} 1 \\ 1\end{bmatrix} \\ &=\alpha_1^2m(2)\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-60e73f64a342cd3405f51ab1c6c20ec7_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\alpha_1 &= \frac{1}{\sqrt{2m}} \\\mu_1 &= \frac{1}{\sqrt{2m}}\begin{bmatrix}1 \\ 1\end{bmatrix} \\\alpha_2 &= \frac{1}{\sqrt{2m}} \\\mu_2 &= \frac{1}{\sqrt{2m}}\begin{bmatrix}1 \\ -1\end{bmatrix} \\\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-28eedb23287fad8f1328f47c54308505_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix} &=\frac{1}{\sqrt{2m}}\begin{bmatrix}1 & 1 \\ 1 & -1\end{bmatrix} \\\begin{bmatrix} \mu \end{bmatrix}^T \begin{bmatrix} m \end{bmatrix} \begin{bmatrix} \mu \end{bmatrix} &= \frac{m}{2m} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \begin{bmatrix} 1 && 0 \\ 0 && 1 \end{bmatrix} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \\&= \frac{1}{2} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \\&= \frac{1}{2}\begin{bmatrix} 2 && 0 \\ 0 && 2 \end{bmatrix} \\&= \begin{bmatrix} 1 && 0 \\ 0 && 1\end{bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2404d3cf5d299086791928733ef4300e_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix}^T \begin{bmatrix} k \end{bmatrix} \begin{bmatrix} \mu \end{bmatrix} &= \frac{1}{2m} \begin{bmatrix} k + k_c && -k_c \\ -k_c && k + k_c \end{bmatrix} \\&= \frac{1}{2m}\begin{bmatrix}1 && 1 \\ 1 && -1\end{bmatrix} \begin{bmatrix} k+k_c && -k_c \\ -k_c && k+k_c \end{bmatrix} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \\&= \begin{bmatrix} \frac{k}{m} && 0 \\ 0 && \frac{(k+k_c)}{m}\end{bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f5a860b89ed020ce304bca817a314ad6_l3.png)
and the transformal equations for free vibration are
![]()
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}\eta_1 &= \eta_1(0)\cos p_1t + \frac{\dot{\eta}_1(0)}{p_1}\sin p_1t \\\eta_2 &= \eta_2(0)\cos p_2t + \frac{\dot{\eta}_2(0)}{p_2}\sin p_2t\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2746e945432bdf13ff9fcc735da4b50f_l3.png)
We transform these back to the original coordinates
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}x_1(t) &= \frac{1}{\sqrt{2m}} \eta_1(t) + \frac{1}{\sqrt{2m}} \eta_2(t) \\x_2(t) &= \frac{1}{\sqrt{2m}} \eta_1(t) - \frac{1}{\sqrt{2m}} \eta_2(t)\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-03355f7fa637fb44d61a241aba2211f9_l3.png)
Assume the initial conditions are:
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix} x(0) \end{Bmatrix} &= \begin{Bmatrix} 1 \\ 0 \end{Bmatrix} \\\begin{Bmatrix} \dot{x}(0) \end{Bmatrix} &= \begin{Bmatrix} 0 \\ 0 \end{Bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-03bc4ebb7506a52dcd20a3d5315ef73b_l3.png)
then:
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix} 1 \\ 0 \end{Bmatrix} &= \begin{bmatrix} \mu \end{bmatrix} \begin{Bmatrix} \eta(0) \end{Bmatrix} \\\begin{Bmatrix} 0 \\ 0 \end{Bmatrix} &= \begin{bmatrix} \mu \end{bmatrix} \begin{Bmatrix} \dot\eta(0) \end{Bmatrix} \\\begin{Bmatrix} x_1(0) \\ x_2(0) \end{Bmatrix} &= \frac{1}{\sqrt{2m}} \begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \begin{Bmatrix} \eta_1(0) \\ \eta_2(0) \end{Bmatrix} \\\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d15a40d20287869fdd74c950a90469af_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}x_1 &= \frac{1}{\sqrt{2m}}\eta_1(0)\cos p_1t + \frac{1}{\sqrt{2m}}\eta_2(0)\cos p_2t \\x_2 &= \frac{1}{\sqrt{2m}}\eta_1(0)\cos p_1t - \frac{1}{\sqrt{2m}}\eta_2(0)\cos p_2t\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-970fd5f56604750011e22d44dd74faf8_l3.png)
We can find the transformed initial conditions from
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix}^{-1}\begin{Bmatrix} x(0) \end{Bmatrix} &=\begin{Bmatrix} \eta(0) \end{Bmatrix} \\\begin{bmatrix} \mu \end{bmatrix}^{-1} &=\frac{\sqrt{2m}}{-2} \begin{bmatrix} -1 && 1 \\ 1 && 1 \end{bmatrix} \\ &=\sqrt{2m} \begin{bmatrix} \frac{1}{2} && -\frac{1}{2} \\ -\frac{1}{2} && -\frac{1}{2} \end{bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-67b624e70f63bc9cb3f2d3a8fa96627e_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix} \eta(0) \end{Bmatrix} &= \sqrt{2m}\begin{bmatrix} \frac{1}{2} && -\frac{1}{2} \\ -\frac{1}{2} && -\frac{1}{2} \end{bmatrix} \begin{Bmatrix} 1 \\ 0 \end{Bmatrix} \\&= \sqrt{2m} \begin{Bmatrix} \frac{1}{2} \\ -\frac{1}{2} \end{Bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e842a47b3ea5dbc79e3fe4d09422e47a_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}x_1(t) &= \frac{1}{2}\cos p_1t + \frac{1}{2}\cos p_2t \\x_2(t) &= \frac{1}{2}\cos p_1t - \frac{1}{2}\cos p_2t\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-436507060e1890a863f97dd940ce60d7_l3.png)
as before.
Now add proportional damping
Select relative damping (proportional to stiffness)
![]()
The transformed equations will be
![]()
but we called ![]()
![]()
The solution to the initial value problem for the case discussed is
![]()
![]()
![]()
![]()
As before
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix} x(t) \end{Bmatrix} &= \begin{Bmatrix} \mu \end{Bmatrix}_1 \eta_1(t) + \begin{Bmatrix} \mu \end{Bmatrix}_2 \eta_2(t) \\x_1(t) &= \frac{1}{\sqrt{2m}}\eta_1(t) + \frac{1}{\sqrt{2m}}\eta_2(t) \\x_2(t) &= \frac{1}{\sqrt{2m}}\eta_1(t) - \frac{1}{\sqrt{2m}}\eta_2(t)\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-eb7718cff50556477d5fae0798499ed5_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}x_1(t) &= \frac{1}{2}e^{-\frac{\beta}{2}p_1^2t}\biggr[\frac{\cos(\sqrt{1-\nu_1^2}p_1t-\Psi_1)}{\sqrt{1-\nu_1^2}p_1}\biggr] + \frac{1}{2}e^{-\frac{\beta}{2}p_2^2t}\biggr[\frac{\cos(\sqrt{1-\nu_2^2}p_2t-\Psi_2)}{\sqrt{1-\nu_2^2}p_2}\biggr] \\x_2(t) &= \frac{1}{2}e^{-\frac{\beta}{2}p_1^2t}\biggr[\frac{\cos(\sqrt{1-\nu_1^2}p_1t-\Psi_1)}{\sqrt{1-\nu_1^2}p_1}\biggr] - \frac{1}{2}e^{-\frac{\beta}{2}p_2^2t}\biggr[\frac{\cos(\sqrt{1-\nu_2^2}p_2t-\Psi_2)}{\sqrt{1-\nu_2^2}p_2}\biggr]\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e4cf952f17bb7577abff87e631fa4ac1_l3.png)
We can now consider the decay of each of these two components using the idea of the so-called logarithmic decrement. Recall from the SDOF case that
![Rendered by QuickLaTeX.com \[ \begin{split}\ln{\frac{X_0}{X_n}} &= \biggr( \frac{2\pi\zeta}{\sqrt{1-\zeta^2}} \biggr)n \\\ln{\frac{X_0}{X_n}} &= \biggr( \frac{2\pi\nu_i}{\sqrt{1-\nu_i^2}} \biggr)n \quad \text{for each mode considered} \\\ln{\frac{X_0}{X_n}} &= \biggr( 2\pi\nu_i \biggr)n \quad \text{for small } \nu_i \\\ln{\frac{X_0}{X_n}} &= 2\pi \frac{\beta}{2}p_i n \\n &= \frac{1}{\pi\beta p_i}\ln{\frac{X_0}{X_n}}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e40813134100ac97891ef2f68da50510_l3.png)
where
Once ![]() is chosen
is chosen ![]() decreases linearly with
decreases linearly with ![]() .
.
If we set ![]()
![Rendered by QuickLaTeX.com \[ \begin{split}\ln{\frac{X_0}{X_n}} &= 2\pi\biggr( \frac{\alpha}{2p_i}\biggr) n \\n &= \frac{p_i}{\pi\alpha}\ln{\frac{X_0}{X_n}}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-79d66666bfac983736558b28fbf766f3_l3.png)
and
Consider a steady-state damped problem
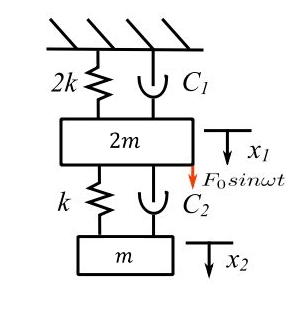
The equations of motion are:
![]()
Consider the undamped problem to find the ![]() and
and ![]()
![Rendered by QuickLaTeX.com \[ \begin{split}(3k-2mp^2)(k-mp^2)-k^2 &= 0 \\p^4-\frac{5}{2}\frac{k}{m}p^2 + \frac{k^2}{m^2} &= 0\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f96a9097de0d9270f01c29a31bfc2baf_l3.png)
therefore:
![]()
![]()
therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}\frac{u_2}{u_1} &= 3-\frac{2m}{k}p^2 \\\biggr( \frac{u_2}{u_1} \biggr)_1 &= 2 \\\biggr( \frac{u_2}{u_1} \biggr)_2 &= -1 \\\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ff3d70ab655bf410114c75f257ae4bb9_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{Bmatrix} u \end{Bmatrix}_1 &= \begin{Bmatrix} 1 \\ 2 \end{Bmatrix} \\\begin{Bmatrix} u \end{Bmatrix}_2 &= \begin{Bmatrix} 1 \\ -1 \end{Bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e883bb979106585450a22cdcada0b91c_l3.png)
To find ![]()
![]()
Therefore ![]()
In the same manner, ![]()
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix} &= \frac{1}{\sqrt{6m}}\begin{bmatrix} 1 && \sqrt{2} \\ 2 && -\sqrt{2} \end{bmatrix} \\\begin{bmatrix} \mu \end{bmatrix}^T \begin{Bmatrix} F_0\sin{\omega t} \\ 0 \end{Bmatrix}&= \frac{\sin{\omega t}}{\sqrt{6m}} \begin{Bmatrix} F_0 \\ \sqrt{2}F_0 \end{Bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3f8a8ab309c2524ada53d42636e05ae8_l3.png)
Therefore undamped differential equations are
![Rendered by QuickLaTeX.com \[ \begin{split}\Ddot{\eta}_1 + p_1^2\eta_1 &= \frac{F_0}{\sqrt{6m}}\sin{\omega t} \\\Ddot{\eta}_2 + p_2^2\eta_2 &= \frac{\sqrt{2}F_0}{\sqrt{6m}}\sin{\omega t}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e2362cc0f1ae91698f833320393d1ad0_l3.png)
The undamped steady state solution is
![Rendered by QuickLaTeX.com \[ \begin{split}\eta_1 &= \frac{F_0}{\sqrt{6m}}\frac{\sin{\omega t}}{(p_1^2-\omega^2)} \\\eta_2 &= \frac{\sqrt{2}F_0}{\sqrt{6m}}\frac{\sin{\omega t}}{(p_2^2-\omega^2)}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7125d1cc9f6addbfd610a6143a465661_l3.png)
As a result the undamped solution is
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}x_1 &= \frac{1}{\sqrt{6m}}\biggr[ \eta_1 + \sqrt{2}\eta_2 \biggr] \\x_2 &= \frac{1}{\sqrt{6m}}\biggr[ 2\eta_1 - \sqrt{2}\eta_2 \biggr]\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-98529d0884d146ff4694326a67993365_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}x_1 &= \frac{F_0\sin{\omega t}}{6m}\biggr[ \frac{1}{(p_1^2-\omega^2)} + \frac{2}{(p_2^2-\omega^2)} \biggr] \equiv X_1\sin{\omega t} \\x_2 &= \frac{F_0\sin{\omega t}}{6m}\biggr[ \frac{2}{(p_1^2-\omega^2)} - \frac{2}{(p_2^2-\omega^2)} \biggr] \equiv X_2\sin{\omega t}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8ab354e1278c4ce988a45acdb93fa3b7_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}X_1 &= \frac{F_0}{6m}\biggr[ \frac{(p^2_2-\omega^2) + 2(p_1^2-\omega^2)}{(p_1^2 - \omega^2)(p_2^2 - \omega^2)} \biggr] \\&= \frac{F_0}{2k} \frac{[\frac{k}{m} - \omega^2 ]}{ (p_1^2-\omega^2) (p^2_2-\omega^2)}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e52fe46f94355a141d5baa695779ca7d_l3.png)
![]()
As was shown previously at ![]()
![Rendered by QuickLaTeX.com \[ \begin{split}X_1 &= 0 \\X_2 &= -\frac{F_0}{k}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ebde9b6b62388f474b0170b0daaf2e37_l3.png)
Now lets add damping
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix}^T \begin{bmatrix} c \end{bmatrix} \begin{bmatrix} \mu \end{bmatrix} &= \frac{1}{6m} \begin{bmatrix} 1 && 2 \\ \sqrt{2} && -\sqrt{2} \end{bmatrix} \begin{bmatrix} c_1+c_2 && -c_2 \\ -c_2 && c_2 \end{bmatrix} \begin{bmatrix} 1 && \sqrt{2} \\ 2 && -\sqrt{2} \end{bmatrix} \\&= \frac{1}{6m} \begin{bmatrix} c_1+c_2(3-\sqrt{2}) && \sqrt{2}c_1-2\sqrt{2}c_2 \\ \sqrt{2}c_1-2\sqrt{2}c_2 && 2c_1 \end{bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-61948a709d0e4a8db542fbd36dd8a5ac_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split}c_1 &= 2c_2 \\ &= 2c \\ c_2 &= c\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-439c3cc97854884928819be8f6168a20_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\begin{bmatrix} \mu \end{bmatrix}^T \begin{bmatrix} c \end{bmatrix} \begin{bmatrix} \mu \end{bmatrix} &= \frac{1}{6m} \begin{bmatrix} (5-\sqrt{2})c && 0 \\ 0 && 2c \end{bmatrix} \\ &= \frac{1}{6m} \begin{bmatrix} \hat{c}_1 && 0 \\ 0 && \hat{c}_2 \end{bmatrix}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b6e3115d1bcfa99f6d28f00b061e5f76_l3.png)
Therefore the equations of motion are:
![Rendered by QuickLaTeX.com \[ \begin{split}\Ddot{\eta}_1 + p_1^2 \eta_1 + \frac{\hat{c}_1}{6m} \dot{\eta}_1 &= \frac{F_0}{\sqrt{6m}} \sin{\omega t} \\\Ddot{\eta}_2 + p_2^2 \eta_2 + \frac{\hat{c}_2}{6m} \dot{\eta}_1 &= \frac{\sqrt{2}F_0}{\sqrt{6m}} \sin{\omega t} \\\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5699c43cef828b19cbf9ef8b33588a54_l3.png)
Consider the standard form where the coefficient of ![]() is
is ![]()
![]()
Therefore
![Rendered by QuickLaTeX.com \[ \begin{split}\nu_1 &= \frac{\hat{c}_1}{12mp_1} \\&= \frac{(5-\sqrt{2})c}{12mp_1} \\\nu_2 &= \frac{c}{6mp_2}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5799562d57e72958d514fe4421fdbf7c_l3.png)
