Review of single and multi-degree of freedom (mdof) systems: Introduction and Review
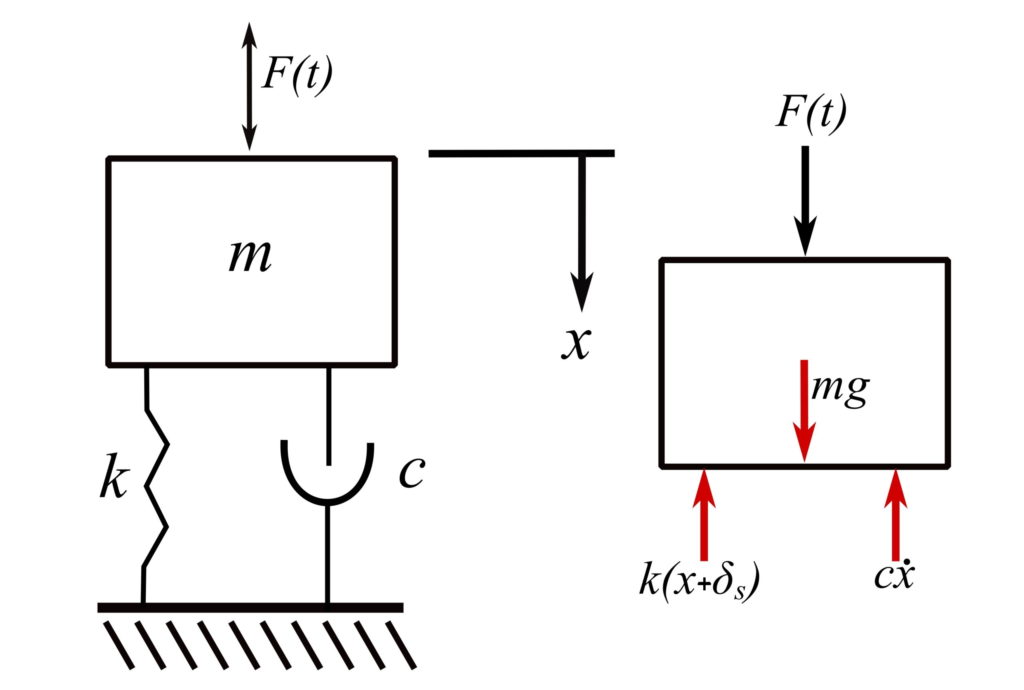
We are interested in small motions about some equilibrium positions. For SDOF systems, ![]() is usually measured from this static equilibrium position.
is usually measured from this static equilibrium position.
![]()
Let ![]() for static equilibrium. Therefore:
for static equilibrium. Therefore:
![]()
Let ![]() . Therefore:
. Therefore:
![]()
All SDOF systems can be reduced to this form (assuming viscous damping):
![]()
Where ![]() means equivalent. To determine the nature of the motion, first consider this linearized equation of free vibration (Note: May have to linearize).
means equivalent. To determine the nature of the motion, first consider this linearized equation of free vibration (Note: May have to linearize).
Assume ![]() (homogeneous), where
(homogeneous), where ![]() is constant and
is constant and ![]() is to be determined.
is to be determined.
![]()
![Rendered by QuickLaTeX.com \[\begin{split}s_{1,2} &= -\frac{c_e}{2m_e} \pm \sqrt{\Big(\frac{c_e}{2m_e}\Big)^2-\frac{k_e}{m_e}}\\&= -\frac{\tilde{c}}{2} \pm \sqrt{\Big(\frac{\tilde{c}}{2}\Big)^2-\tilde{k}}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-18640f3d82dd9e04d6c54030b2b09fae_l3.png)
If ![]() are real and negative, then
are real and negative, then ![]() as
as ![]() . If either of
. If either of ![]() or
or ![]() are real and positive, then the solution increases with time.
are real and positive, then the solution increases with time.
If ![]() are complex, then they are complex conjugates and the nature of the motion depends on the real part. If the real part is negative,
are complex, then they are complex conjugates and the nature of the motion depends on the real part. If the real part is negative, ![]() as
as ![]() . If positive,
. If positive, ![]() as
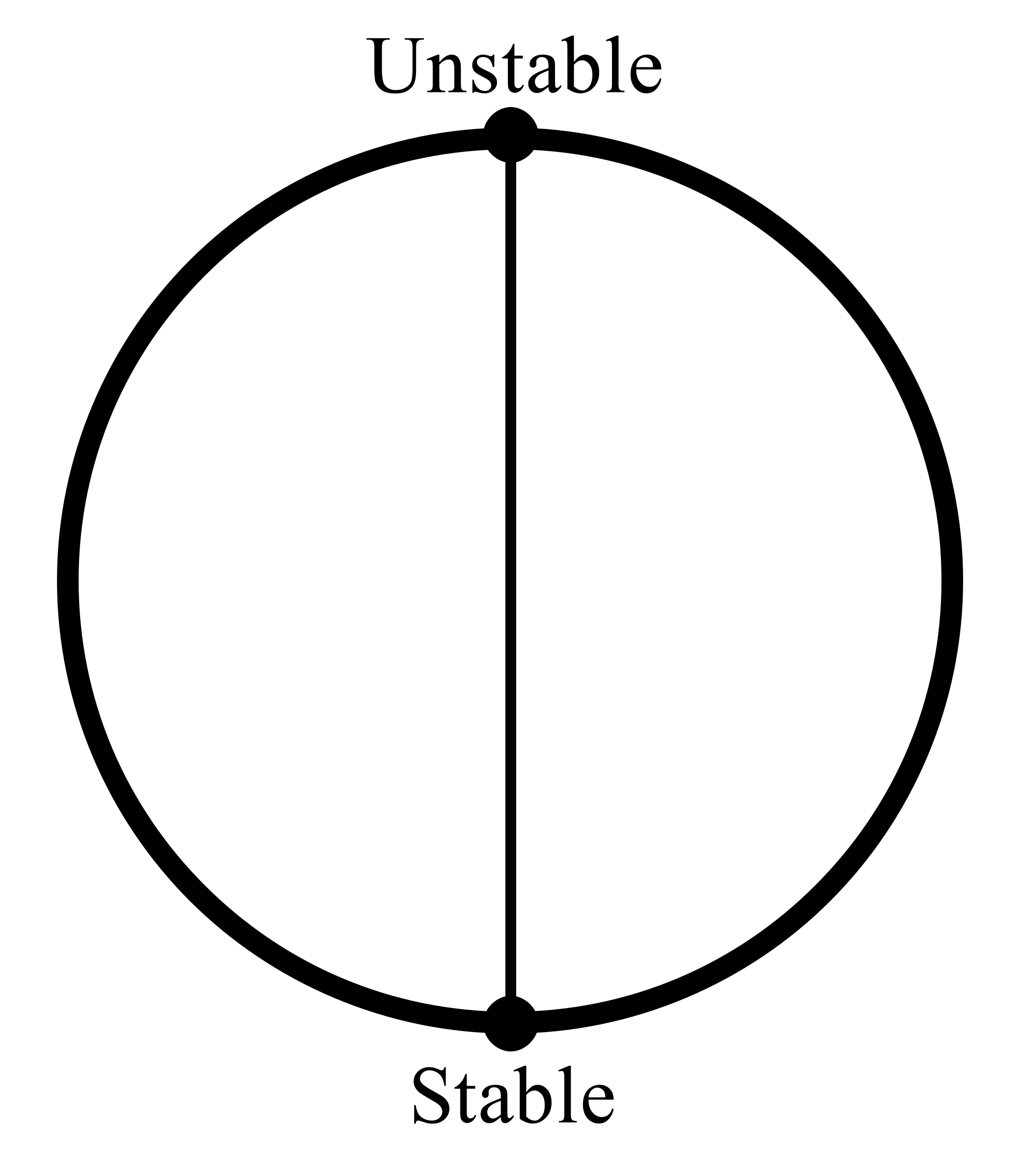
as ![]() . If the real part is zero, the motion is oscillatory and this is the borderline case between stability and instability.
. If the real part is zero, the motion is oscillatory and this is the borderline case between stability and instability.
Consider all cases:
 . The roots have a negative real part and is stable regardless of
. The roots have a negative real part and is stable regardless of 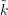 . If
. If 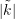 is larger than
is larger than 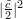 , there will be an oscillatory part, but
, there will be an oscillatory part, but 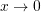 as
as 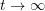 . This is called asymptotically stable.
. This is called asymptotically stable.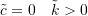 . The roots are imaginary, and the system is borderline stable.
. The roots are imaginary, and the system is borderline stable. . The roots have a positive real part, or are complex conjugates. Therefore, the system is unstable.
. The roots have a positive real part, or are complex conjugates. Therefore, the system is unstable. One root has a positive real part. Therefore the system is unstable. The damping cannot overcome the negative spring.
One root has a positive real part. Therefore the system is unstable. The damping cannot overcome the negative spring. . The roots have a positive real part, and therefore the system is unstable. Negative damping feeds energy into the system.
. The roots have a positive real part, and therefore the system is unstable. Negative damping feeds energy into the system.
Consider the solution for free damped vibration:
![]()
Drop ![]() , but remember that
, but remember that ![]() ,
,![]() ,
,![]() are equivalent. Thus:
are equivalent. Thus:
![]()
Again, assume that ![]() . Thus:
. Thus:
![]()
The critical value is then when:
![]()
Alternatively:
![]()
Define ![]() . Then:
. Then:
![]()
Thus:
![]()
Where ![]() is the damping ratio (system parameter).
is the damping ratio (system parameter).
Assuming ![]() :
:
![]()
And using ![]() :
:
![]()
Using initial conditions ![]() ,
, ![]() , we get the following:
, we get the following:
![]()
We can write this as:
![]()
Where ![]() ,
, ![]() , and
, and ![]() .
.
In some problems, we have to find the equilibrium (static) configurations and then determine the motion about these positions.
Example
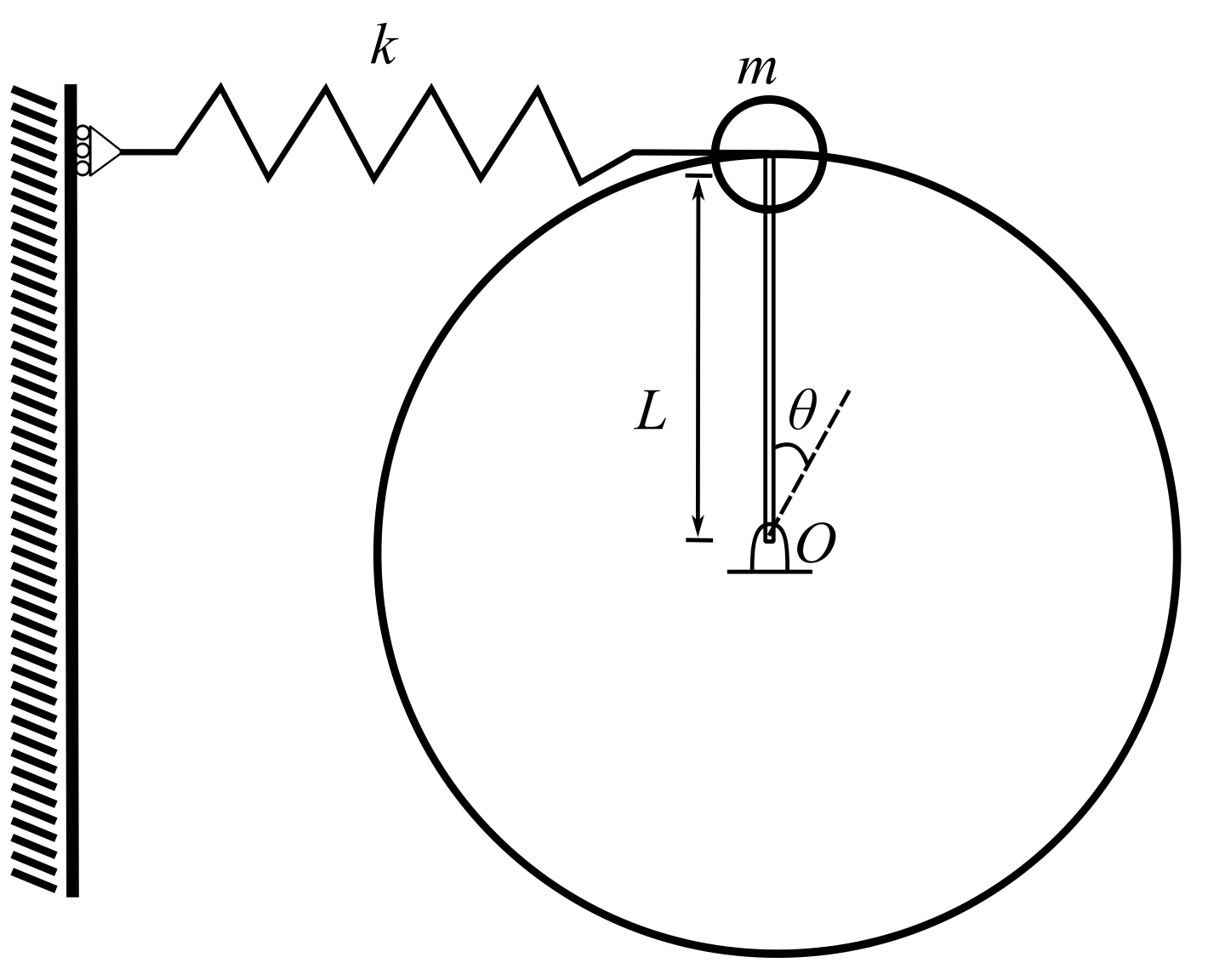
Find the motion about the equilibrium configuration.
![]() slides on a wire with viscous friction
slides on a wire with viscous friction ![]() .
.
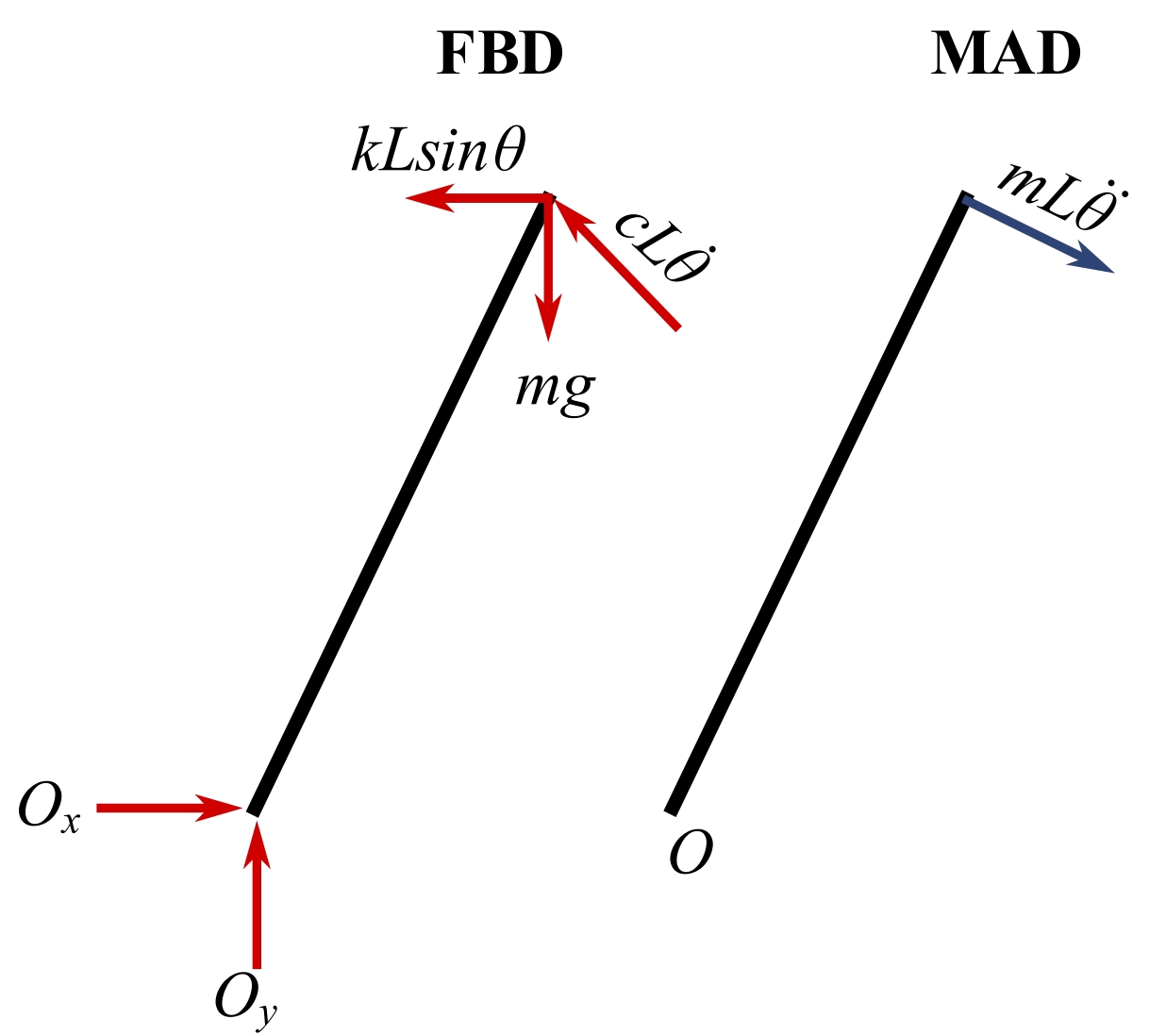
Solution
![]()
![]()
![]()
We must find static equilibrium configurations and determine equation of motion for small perturbations about these static configurations.
Set ![]() , and let
, and let ![]() . Therefore:
. Therefore:
![]()
![]()
Therefore. the static configurations are given by:
![]()
Assuming ![]() , there are 3 positions.
, there are 3 positions.
To find the motion, linearize (1) about ![]() . Set
. Set ![]() , where
, where ![]() is a small angle.
is a small angle.
![]()
![]()
Put the above into the original equation of motion to get:
![]()
Note that ![]() .
.
![]()
Using the fact that the ![]() term is small compared to 1, it becomes:
term is small compared to 1, it becomes:
![]()
![]()
The above equation looks like the standard form except for a constant term that is zero for all conditions.
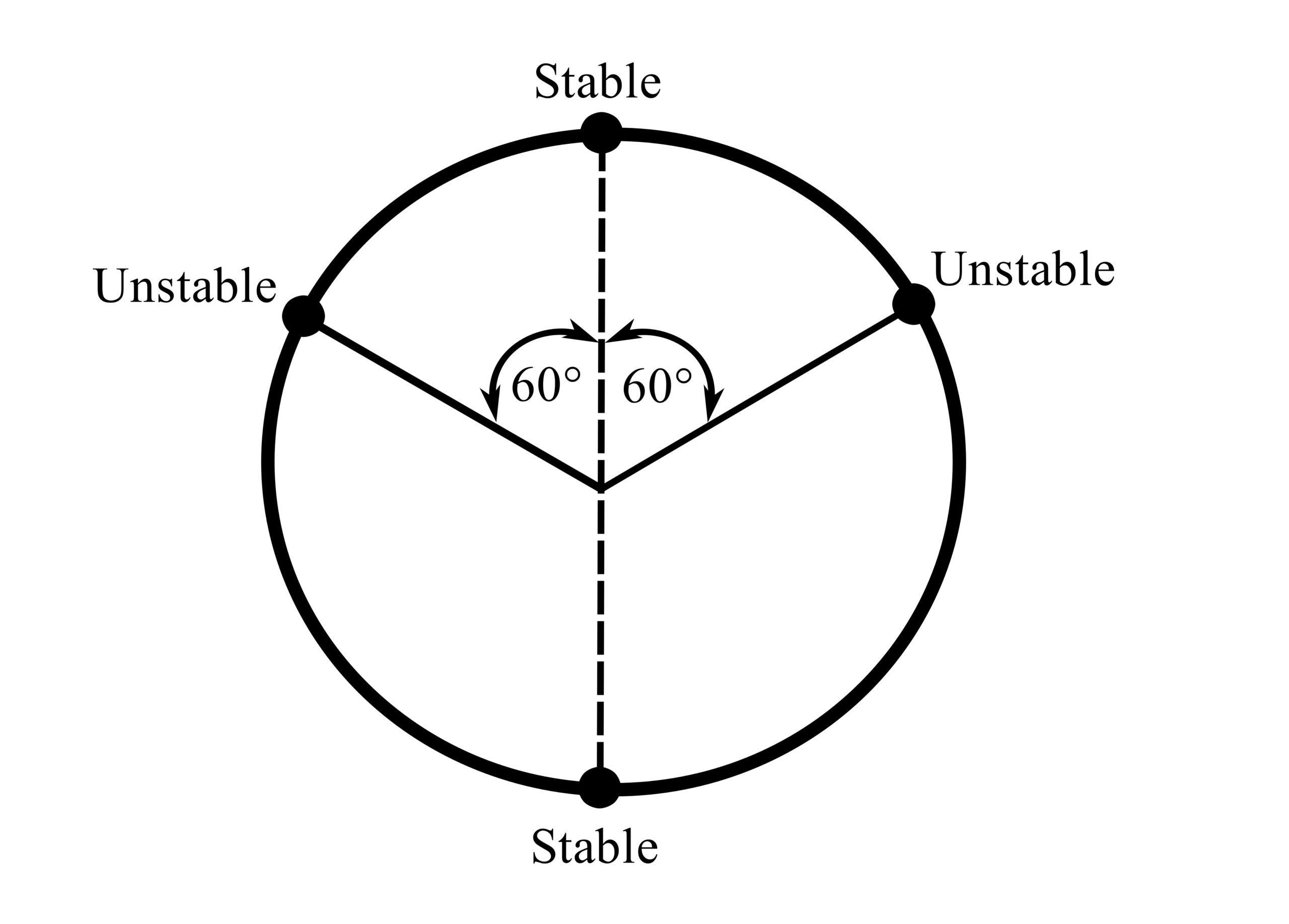
Now consider all three positions:
1. ![]() .
.
![]()
Therefore, this is stable if ![]() as
as ![]() , but unstable if
, but unstable if ![]() .
.
2.![]() .
.
![]()
Therefore, this is always stable.
3.![]() .
.
![]()
![]()
Therefore, this is always unstable, regardless of damping.
Example
1.![]() ,
, ![]() ,
, ![]() . Therefore:
. Therefore:
![]()
2.![]() ,
, ![]() . Therefore:
. Therefore:
![]()