Review of single and multi-degree of freedom (mdof) systems: Energy Considerations in Vibrations
For many dynamic/vibration systems energy considerations are useful especially in modelling. This becomes evident when the complexity of the system increases as the formulation of the models will usually involve velocities rather than accelerations and the kinematics for general motion are easier to describe. Specifically for vibrations we can appreciate the exchange of energy occurring between the kinetic and potential components with the damping providing the energy dissipation. This occurs in the consideration of the Lagrange formulation of dynamical systems
If we choose the static equilibrium position as the datum for the energy calculation we must be aware of the energy involved in the static equilibrium deflection. There will be instances in which the static condition does not have a deflection then the energy calculation must include consideration of the position of the mass of the system.
One DOF Spring Oscillator
For a single DOF undamped system we can calculate the natural frequency from energy considerations as we know the motion is Simple Harmonic Motion (SHM). In addition it is possible to use energy as an approach to finding approximate solutions for the natural frequency without a large computational effort. For these systems, termed conservative, the sum of the kinetic and potential energy for free vibration is a constant.
T (kinetic) + U (potential) = C (constant)
In addition the energy varies over time from being all potential to all kinetic so that
![]()
Under the assumed SHM ![]()
Consider the SDOF system from an energy perspective where again ![]() is measured from the static equilibrium configuration.
is measured from the static equilibrium configuration.

Potential energy is the work done by F in moving through ![]() (energy in spring) :
(energy in spring) :
![]()
![]()
While the change in potential energy due to position of ![]() is
is ![]() . Therefore, the total potential energy is
. Therefore, the total potential energy is ![]() , assuming :
, assuming :
![]()
![]()
![]()
Therefore,
![]()
![]()
We can extend this idea to consider approximating the effect on the natural frequency when the mass of the spring is included. Assume that the spring of length ![]() has a uniform mass
has a uniform mass ![]() over its length. Then at any position on the spring the velocity is
over its length. Then at any position on the spring the velocity is ![]() and the kinetic energy of an infinitesimal mass
and the kinetic energy of an infinitesimal mass ![]() is
is ![]() and the kinetic energy of the spring is:
and the kinetic energy of the spring is:
![]()
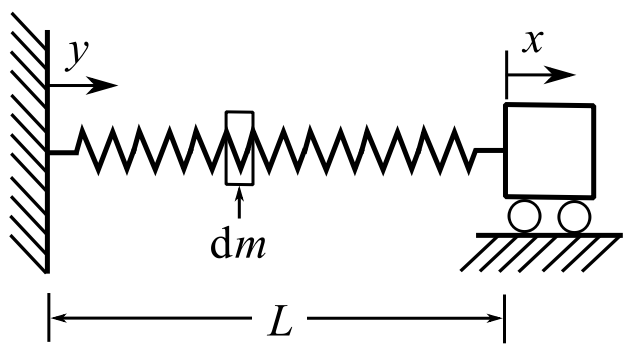
If we now make an assumption of how the spring “moves” we can calculate ![]() e.g. assume the spring displaces linearly with position y so that at
e.g. assume the spring displaces linearly with position y so that at ![]()
![Rendered by QuickLaTeX.com \[ \begin{split} T_\text{spring} &= \frac{1}{2} \frac{M}{L^3} \int_{0}^{L} (\dot{x} y)^2 \,dy \\&= \frac{1}{2} \frac{M}{L^3} \frac{L^3}{3} \dot{x}^2 \\&= \frac{1}{2} \frac{M}{3} \dot{x}^2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b8fc7587e8a0935b0d86ec5014169d04_l3.png)
Now using ![]() :
:
![]()
![]()
If instead we assumed the “spring” was a simply supported beam of mass ![]() and length
and length ![]() and that the dynamic shape is a half-sine then at any position the velocity is:
and that the dynamic shape is a half-sine then at any position the velocity is: ![]() and the mass/unit length is
and the mass/unit length is ![]()
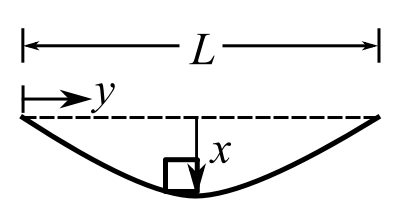
![Rendered by QuickLaTeX.com \[\begin{split} T_\text{spring} &= \frac{1}{2} \int_{0}^{L} \frac{M}{L}\big(\dot{x}\big)\strut^2 \big(\sin \frac{\pi y}{L}\big)\strut^2 \,dy \\&= \frac{1}{2} \frac{M}{L}(\dot{x})^2 \bigg[\frac{y}{2} - \frac{L^2}{4 \pi ^2} \sin \frac{2 \pi y}{L} \bigg] \biggr|_ 0^L \\&= \frac{1}{2} \frac{M}{2} \dot{x}^2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-98e1b7b4198bec625c7507dd4164d48c_l3.png)
Then using the same approach:
![]()
