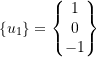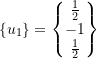Review of single and multi-degree of freedom (mdof) systems: Applications of MDOF systems
The concept of modes and their corresponding natural frequencies is useful in understanding the behavior of lightly damped systems. Before adding the complication of damping to our models, we will consider several applications to industrial situations.
Example
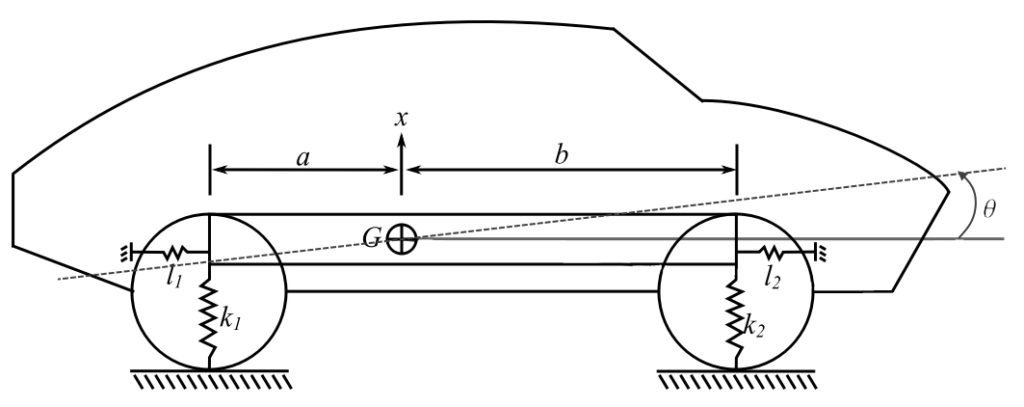
The model of the automobile shown is used to predict the low frequency modes of vibrations as these are responsible for the low frequency noise in the passenger compartment. Knowing these models can assist the designer in controlling them. In addition, it helps the designer in predicting the response of the frame to various inputs from road irregularities. As an initial estimate, the three modes of vibration of the vehicle may be considered as uncoupled. For the specific case below, the assumption of uncoupled modes is to be compared to the coupled model.
a) For the longitudinal model of the vehicle, specialize the equations of motion for the case of ![]() (see previous section).
(see previous section).
b) If any of the modes are uncoupled determine an expression of the natural frequency. For the coupled modes derive the equations of motion for free vibration starting from Newton’s laws.
c) Calculate the natural frequencies and mode shapes for the two coupled modes of vibration. The weight of the vehicle is ![]() and the radius of gyration on the vehicle about
and the radius of gyration on the vehicle about ![]() is
is ![]() .
.
Solution
a)
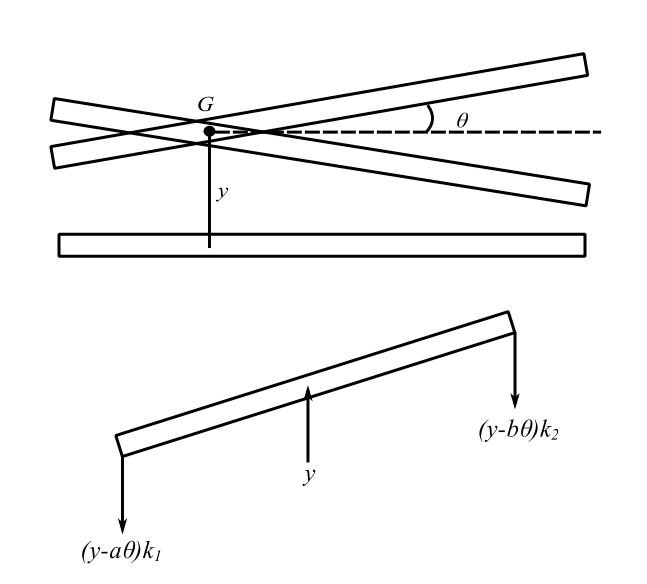
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & J_G \end{bmatrix}\begin{Bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{\theta} \end{Bmatrix} + \begin{bmatrix} \ell_1 + \ell_2 & 0 & 0 \\ 0 & k_1 + k_2 & k_2b - k_1a \\ 0 & k_2b-k_1a & k_1a^2 + k_2b^2 \end{bmatrix}\begin{Bmatrix} x \\ y \\ \theta \end{Bmatrix} = \begin{Bmatrix} 0 \\ 0 \\ 0 \end{Bmatrix} (+)\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-89f3ea6139fd352075249f450fb6dd0e_l3.png)
b)
For horizontal motion:
![]()
Therefore:
![]()
![]()
![]()
![]() &
& ![]() are the same as
are the same as ![]() .
.
c)
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![]()
Assume ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
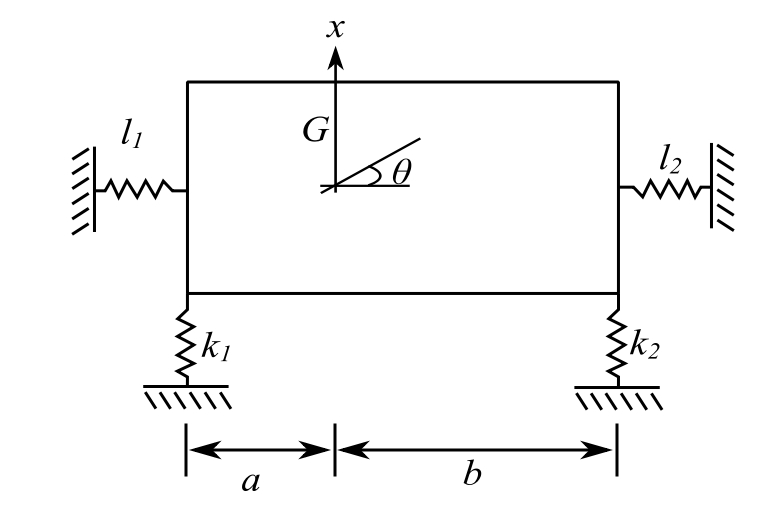
![Rendered by QuickLaTeX.com \[\begin{split} p_1^2 &=40.74 \\ p_2^2 &=78.65 \\ p_{1,2} &= 6.38 \ \text{rads/s}, 8.87 \ \text{rads/s} \\ &= \underline{\underline{1.01 \ \text{Hz}}}, \underline{\underline{1.41 \ \text{Hz}}} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cf95d1f33f0b64224130b7c6bc34721d_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\begin{split} \frac{X}{\Theta} &= \frac{(k_1a-k_2b)}{k_1+k_2-mp^2} \\ & \\ \Big(\frac{X}{\Theta}\Big)_1 &= \frac{(k_1a-k_2b)/m}{\frac{(k_1+k_2)}{m}-p^2} \\ &= \frac{[(2200)(45)-2700(5.5)]\frac{32.2}{3550}}{(44.45)-40.74} \\ &= \underline{\underline{-12.1 \ \text{ft/rad}}} \\ & \\ \Big(\frac{X}{\Theta}\Big)_2 &= \frac{-44.90}{44.45-78.65} \\ &= \underline{\underline{1.31}} \text{ft/rad}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bb4130f76f47c5756552b38bc48f1e1d_l3.png)
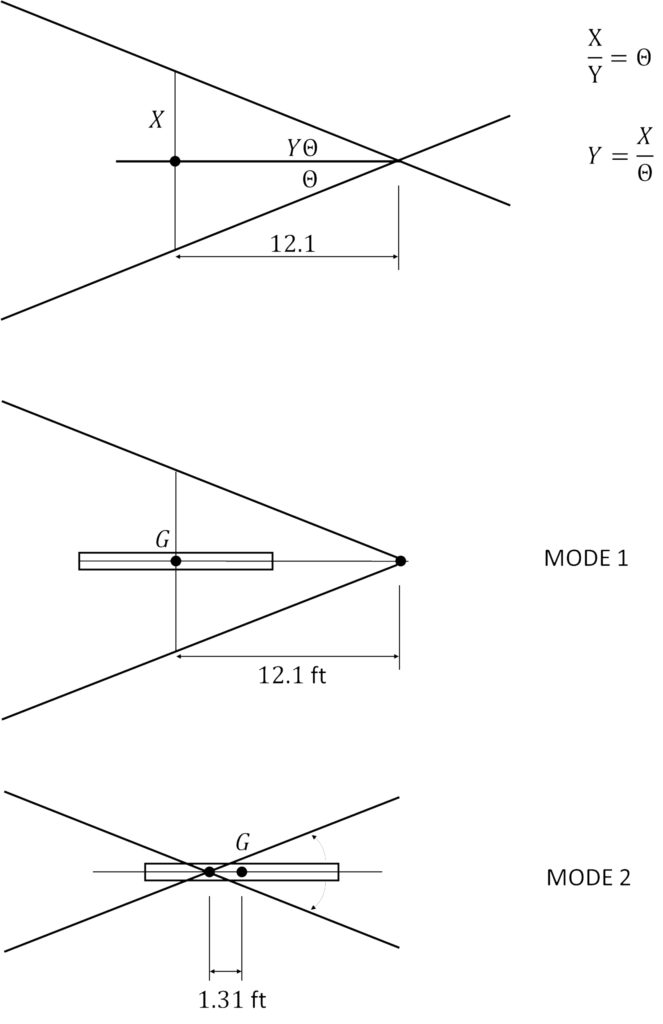
If we “uncoupled” the modes
Assume vertical node is
![Rendered by QuickLaTeX.com \[\begin{split} p_1 &= \sqrt{\frac{k_1+k_2}{m}} \\ &= \sqrt{\frac{4900*32.3}{3550}} \\ &= 6.67 \ \text{rads/s} \\ &= \underline{\underline{1.06 \ \text{Hz}}} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-aae8a518ff8f459e17462de1a0406d1e_l3.png)
Rotational Mode
![Rendered by QuickLaTeX.com \[\begin{split} p_2 &=\sqrt{\frac{k_1a^2+k_2b^2}{m\vec{r}^2}} \\ &= \sqrt{\frac{[(2200)(4.5)^2+(2700)(5.5)^2]32.2}{3550(4)^2}} \\ &= 8.46 \ \text{rads/s} \\ &= \underline{\underline{1.35 \ \text{Hz}}} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-60c99da2cc7ed2fc374705243466c3a1_l3.png)
If the horizontal stiffness, ![]() , were the same as the vertical then the third frequency,
, were the same as the vertical then the third frequency, ![]() , would be the same as the vertical.
, would be the same as the vertical.
The assumption of uncoupling gives essentially the same answer.
Example
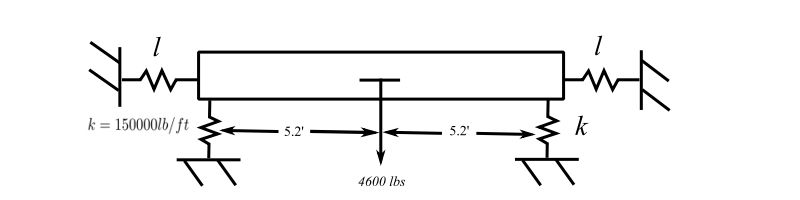
The illustration shows the detail of the proposed isolation system for the reciprocating compressor and motor considered previously and modelled as a single dof system. The actual system does not have the center of gravity symmetrically located on the supporting structure and isolation springs. In situations like these the industrial installation guides recommend that the isolation springs be selected so that the vertical static deflection of all springs is the same. The reason stated is that this will tend to reduce the frequency of the “rocking motions”. This exercise is to investigate this idea as well as the differences found for the isolation of the system compared with the single degree approximation used earlier. More details of the installation are given below. The stiffnesses shown are representative of both springs at the ends of the supports with the lateral stiffnesses assumed to be equal to the vertical values.

a) If the vertical static deflection of the spring is the same what is the ratio of ![]() and
and ![]() ?
?
![]()
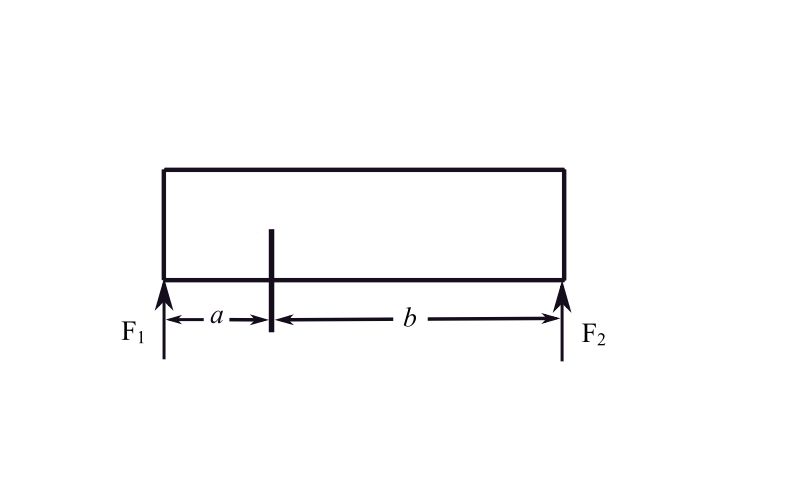
For static equilibrium
![Rendered by QuickLaTeX.com \[\begin{split} F_1a &=F_2b \\ \frac{F_1}{k_1} &= \frac{F_1(\frac{a}{b})}{k_2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6a43609dc24704c42f0bf596031757dc_l3.png)
therefore:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{k_2}{k_1} &=\frac{a}{b} \\ k_2b &= k_1a \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f843b0cf598cf7b6822ca311d00c2224_l3.png)
(b) Under this assumption what happens to the equations of motion?
![Rendered by QuickLaTeX.com \[\begin{bmatrix} m & 0 & 0 \\0 & m & 0 \\ 0 & 0 & m\vec{r}^2 \end{bmatrix}\begin{Bmatrix}\Ddot{x} \\ \Ddot{y} \\ \Ddot{\theta}\end{Bmatrix} + \begin{bmatrix} \ell_1 + \ell_2 & 0 & (\ell_1+\ell_2)h \\0 & k_1+k_2 & 0 \\(\ell_1+\ell_2)h & 0 & h^2(\ell_1+\ell_2)+k_1a^2+k_2b^2\end{bmatrix}\begin{Bmatrix}x \\ y \\ \theta\end{Bmatrix} = \begin{Bmatrix}0\end{Bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9d30ddb78329ba918b26732662ebf1bf_l3.png)
as the vertical mode is uncoupled from the other two
![]()
becomes
![]()
(c) Noting that the original had an operating speed of 1750 RPM and the original transmissibility was 1/15, calculate ![]() for this installation assuming
for this installation assuming ![]()
![]()
therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\omega}{p_v} &=4 \\ p_v &=\frac{1750}{4} \\ &=437.5 \ \text{RPM} \\ &= \frac{437.5*2\pi}{60} \\ &=45.8 \ \text{rads/s} \\ &=7.3 \ \text{Hz} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-eafc539344342a66674b56d4d835e3d9_l3.png)
therefore:
![Rendered by QuickLaTeX.com \[\begin{split} \sqrt{\frac{(k_1+k_2)32.2}{4600}} &=45.8 \\ k_1 + k_2 &= (45.8)^2\frac{4600}{32.2} \\ &=300,000 \text{ lb/ft} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7c9a35a25a517f1b175a265dc0c1de3d_l3.png)
therefore:
![Rendered by QuickLaTeX.com \[\begin{split}k_1+k_1\frac{a}{b} &=k_1\Big(1+\frac{3.5}{6.9}\Big) \\ &=300,000 \text{ lbs/ft} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f06183740d95c3ca57185cf16026938f_l3.png)
![]()
![]()
(d) Assuming SSHM
![]()
![]()
![]()
therefore:
![]()
Divide by
![]()
therefore:
![Rendered by QuickLaTeX.com \[\begin{split}p^4 &-p^2\biggr[\frac{\ell_1+\ell_2}{m}+\frac{\ell_1+\ell_2}{m}\frac{h^2}{r^2}+\frac{k_1}{m}\frac{a^2}{r^2}+\frac{k_2}{m}\frac{b^2}{r^2}\biggr] \\ &+ \frac{(\ell_1+\ell_2)^2}{m^2}\frac{h^2}{r^2} + \frac{(\ell_1+\ell_2)}{m}(\frac{k_1}{m}\frac{a^2}{r^2}+\frac{k_2}{m}\frac{b^2}{r^2}) - \frac{(\ell_1+\ell_2)^2}{m^2}\frac{h^2}{r^2} = 0 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-208897f2f60de7b28a26e512a06ef16b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}p^4 &-p^2\biggr[\frac{(300,000)}{4600}\Big(1+\Big(\frac{0.8}{2.1}\Big)\strut^2\Big)32.2+\frac{181,600}{4600}\Big(\frac{3.5}{2.1}\Big)\strut^2\Big(32.2\Big)+\frac{118,400}{4600}\Big(\frac{6.9}{2.1}\Big)\strut^2 32.2\biggr] \\ &+ \frac{300,000}{(4600)^2}\biggr[181,600\Big(\frac{3.5}{2.1}\Big)\strut^2+118,400\Big(\frac{6.9}{2.1}\Big)\strut^2\biggr](32.2)^2 = 0\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3d40fb8bc46385e727ea5f4f6f924b6e_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} p^2 &= 7470 \pm 5429 \\ & \\ p_1 &= 45.2 \ \text{rads/s (7.2 Hz)} \\ p_2 &= 113.6 \ \text{rad/s (18.1 Hz)} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-be4682a49c5f9168493d6462c6824f0a_l3.png)
(e)
![]()
The rotational mode can be calculated starting from a FBD
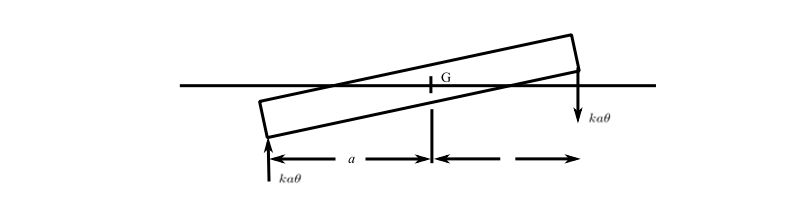
![]()
therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} P^2_{\theta} &= \frac{2ka^2}{mr^2} \\ &= \frac{300,000(5.2)^2(32.2)}{4600(2.1)^2} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0f3d495dd21050dbece95316cf32644a_l3.png)
![]()
(f) Do the calculation using a program
(g) From d)
![Rendered by QuickLaTeX.com \[ \begin{split} p_v &=7.3 \ \text{Hz} \\ (p_H)_1 &= 7.2 \ \text{Hz} \\ (p_{\theta})_2 &= 18.1 \ \text{Hz} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fc6ccb181bd14d64edcd0dcb6958fc76_l3.png)
from e)
![Rendered by QuickLaTeX.com \[ \begin{split} p_v &= 7.3 Hz \\ p_H &= 7.3 Hz \\ p_{\theta} &= 18.1 Hz \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1c765d5e195ff77b30a5b669eb1afbe5_l3.png)
from (f)
![Rendered by QuickLaTeX.com \[ \begin{split} (p)_{v_1} &= ? \\ (p_H)_2 &= ? \\ (p_{\theta})_3 &= ? \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-36f8c7270a1d44cbc06c9b9b4ac22b50_l3.png)
The results show that because ![]() is small compared to
is small compared to ![]() and
and ![]() that there is little difference. The “rotational” (
that there is little difference. The “rotational” (![]() ) is very much higher than the other two and closer to the excitation frequency of 29.2 Hz (1750 RPM).
) is very much higher than the other two and closer to the excitation frequency of 29.2 Hz (1750 RPM).
To lower it, the spacing of the supports would have to be reduced. For example if it were brought to 1/2 of original (5.1′ instead of a total of 10.4′) then the rotational natural frequency would be
![]()
It is obvious from this calculation that the rule of thumb should be that the spacing should be no more than twice the radius of gyration of the total mass!
Example
A commercial front loading washing machine is being used by a spa located adjacent to a medical clinic in a strip mall. During the spin cycle of the washing machine the fluctuating force due to the imbalance of the load causes the floor to vibrate and induces unacceptable levels of noise in the clinic. To reduce this disturbance, an engineering consultant recommends using spring isolation between the washing machine and the floor to reduce the dynamic force transmitted to 20% of the exciting force. The specifications of the washing machine are summarized below. Assume only vertical vibration and neglect damping.
| Net weight | 1049 lbs |
| Maximum load | 255lbs |
| Maximum Dynamic Force | 212 lbs |
| Spin Speed (Frequency of Dynamic Force) | 950 RPM (15.8 Hz) |
| Cylinder Diameter | 27.6 inch |
a) Calculate the appropriate spring constant for each of four springs used to mount the washing machine to meet the specification for the transmissibility and select them from the enclosed table.
b) This washing machine can also be run at a spin speed of 750 RPM. Calculate the Dynamic Force at this RPM and then calculate the force transmitted to the supporting structure compared with the force transmitted at 950 RPM.
c) Using the size of the rotating wash cylinder estimate the unbalanced weight in the maximum load.
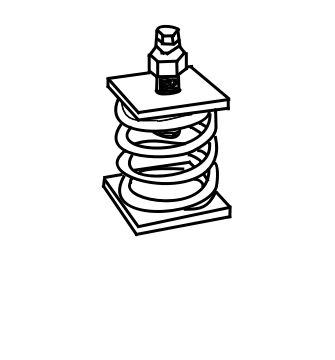
| Mount No. | Mount Constant ( | Load at 2-in. Deflection ( |
| SLF-401 | 50 | 100 |
| SLF-402 | 70 | 140 |
| SLF-403 | 90 | 180 |
| SLF-404 | 115 | 230 |
| SLF-405 | 150 | 300 |
| SLF-406 | 200 | 400 |
| SLF-407 | 305 | 610 |
| SLF-408 | 365 | 730 |
| SLF-409 | 500 | 1,000 |
| SLF-410 | 650 | 1,300 |
| SLF-411 | 740 | 1,880 |
| SLF-412 | 1,150 | 2,300 |
| SLF-413 | 1,500 | 3,000 |
| SLF-414 | 2,000 | 4,000 |
| SLF-415 | 2,680 | 5,360 |
| SLF-416 | 3,500 | 7,000 |
| SLF-417 | 4,750 | 9,500 |
| SLF-418 | 6,250 | 12,500 |
| SLF-419 | 8,200 | 16,400 |
| SLF-420 | 11,250 | 22,500 |
| SLF-421 | 15,000 | 30,000 |
| SLF-422 | 20,000 | 40,000 |
a)
![]()
![Rendered by QuickLaTeX.com \[\begin{split} T &= 0.2 \\&= \frac{1}{(\frac{\omega}{p})^2-1} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-da32275cc0d05a7efcc311c84cda7fc7_l3.png)
Therefore,
![]()
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\omega}{p} &= \sqrt{6} \\&= 2.44 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e9537b3bc663690a9bd2d40af75ef91e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} p &= \frac{\omega}{\sqrt{6}} \\&= \frac{950\cdot(2 \pi)}{60 \sqrt{6}} \\&= 40.61 \ \text{rad/s} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5759ee74bb73d1f2809a9c72d09b3c33_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} k &= p^{2}M = (40.61)^{2} \\&= (40.61)^{2}\Big(\frac{1304}{386}\Big) \\&= 5571.3 \ \text{lb/in} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fc316d5c30743d13d53f3d777cf2d612_l3.png)
Therefore, each spring has
![Rendered by QuickLaTeX.com \[\begin{split} k &= \frac{5571.3}{4} \\&= 1393 \ \text{lbs/in} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2b2e2e78f54f8a38f4b43d01de56f08a_l3.png)
Therefore, SLF 412 as 413 would not meet the transmissibility spec.
b)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} T_{750} &= \frac{1}{6\big(\frac{75}{95}\big)^{2}-1} \\&= 0.365 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-93cff2962633aed80ed05048034de538_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} F_{o-750} &= 212\Big(\frac{75}{96}\Big)^{2} \\&= 132\ \text{lbs} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3d5be0441e0aa19bd58fa5920ffbe8a2_l3.png)
![]()
![]()
Therefore slightly higher than at 950 RPM
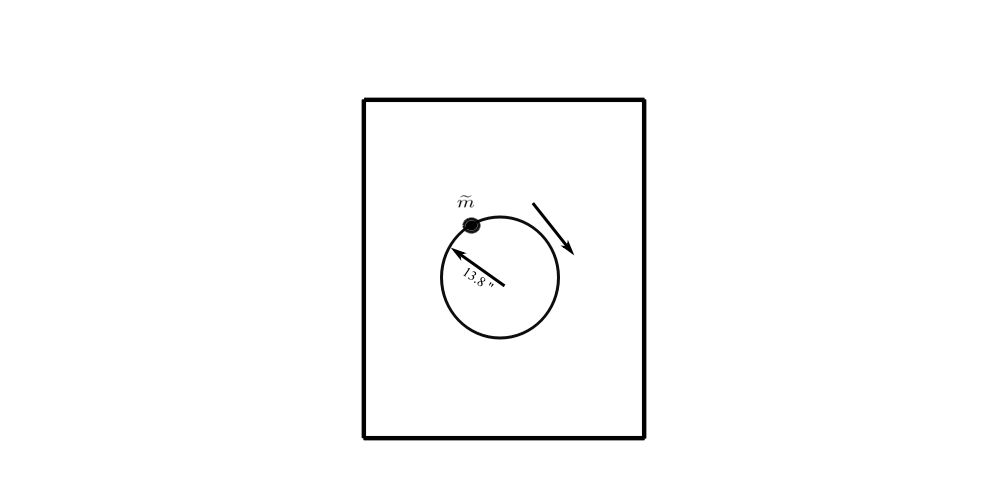
c)
![Rendered by QuickLaTeX.com \[\begin{split} \text{Dynamic Force} &= \tilde{m}e\omega^{2} \\&= \frac{W_{im}}{g}e\omega^{2} \\&= \frac{W_{im}}{386}(13.8)(15.2\cdot2\pi)^{2} \\&= 212 \ \text{lbs} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3938b83a8e8ba7f06509d68e5b6702d2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} W_{im} &= \frac{(212)(386)}{(13.8)(15.2\cdot2\pi)^{2}} \\&= 0.60 \ \text{lbs} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a7c2a89e40a07986a11456f12602a8a5_l3.png)
Perhaps a wet hand towel out of balance
The commercial washer above was considered under the assumption that the vibration was only a vertical mode. However the excitation due to rotating imbalance would cause excitation both horizontally and vertically that would excite coupled modes as well. As a result it is necessary to consider all the planar modes of vibration to investigate if they are near the excitation frequency. The diagram of the dryer is shown below. The lateral stiffness of the supporting springs is estimated to be 0.8 of the vertical stiffness. The excitation frequency is 950 rpm.

![]()
![]()
![]()
![]()
![]()
![]()
a) Specialize the equations of motion for the case shown in the above diagram
b) Determine if any of the modes are uncoupled. For the coupled modes derive the equations of motion for free vibration starting from Newton’s laws.
c) Calculate the natural frequencies and mode shapes for the dryer.
d) If the supports for the dryer were redesigned to make loading easier with h = 0 (as illustrated) what are the natural frequencies compared to the original design. How do they compare with the excitation frequency?

a)
b) Therefore ![]() ,
,![]()
The vertical mode is uncoupled

![]()
![]()
Therefore
![]()
![]()
Which matches the reduction of the general case where ![]() has been replaced by
has been replaced by ![]() and
and ![]() by
by ![]()
c) Calculate the natural frequencies and mode shapes for the dryer
The vertical mode is as previously
![Rendered by QuickLaTeX.com \[\begin{split} p_v &= \sqrt{\frac{2k}{m}}_\text{eff} \\&= \sqrt{\frac{4\cdot1150\cdot386}{(1049+255)}} \\&= 36.90 \ \text{rad/s} \\&= 5.98 \ \text{Hz} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d62ed83fa96d9abe6f78c02c55c9d436_l3.png)
which is well below the excitation frequency of 950RPM (15.8Hz)
Assume that
![]()
![]()
![]()
Therefore
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} p^{2}_{1,2} &= -\frac{7070}{2} \pm \sqrt{\Big(\frac{7070}{2}\Big)^{2}-2379851} \\&= 3535 \pm 3180 \\&= 354,6715 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-292f96c8bb14e4a0c45a64799173ad34_l3.png)
![]()
Mode Shapes
![]()
Therefore
![Rendered by QuickLaTeX.com \[\begin{split} \frac{X}{\Theta} &= \frac{-4\ellh}{(4\ell-mp^{2})} \\&= \frac{-h}{1-\frac{m}{4\ell}p^{2}} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-923b08b137d04d822cf8568f6dca1937_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} \frac{X}{\Theta}\Big|_{1} &= \frac{-28}{1-\frac{(1049+255)(354)}{386(4)(0.8)(1150)}} \\&= -28.3 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ff0259eb5515a1d9ec419cab2514660e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} \frac{X}{\Theta}\Big|_{2} &= \frac{-28}{1-\frac{(1304)(6715)}{386(4)(0.8)(1150)}} \\&= 5.42 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-295d5a55460538cf29ff3f729cc91a6b_l3.png)
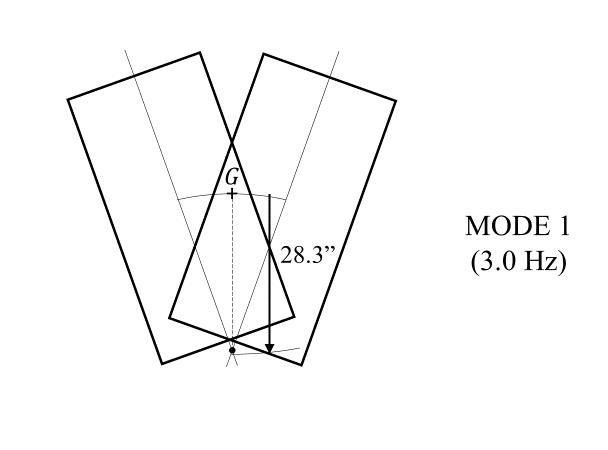
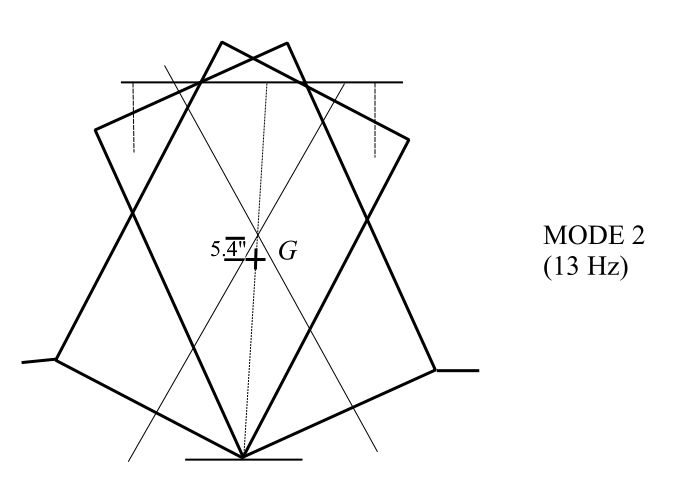
d)

![]()
![]()
![]()
![]()
![]()
![]()
now all natural frequencies are all below the excitation frequency of 158Hz (950RPM)
Semi-Definite Systems – Rigid Body Modes
So far we have dealt with systems that have positive definite stiffness and mass matrices. This means the eigenvalues are positive & real. We can then define an orthonormal basic system. However consider the example
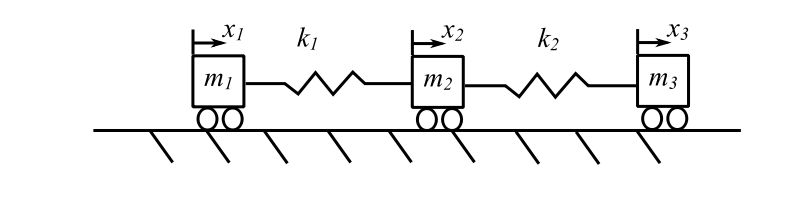
but the stiffness matrix is not positive definitive. It is singular. This is because one “natural frequency” is zero.
![]()
![]() is called a zeroth mode
is called a zeroth mode
Therefore
but since ![]() is positive definite
is positive definite ![]() , therefore
, therefore ![]() ,
, ![]()
and the system is simply moving off in one direction. To suppress this mode we set:
![]()
This is the constraint equation:
![]()
or
![]()
Where this expression says the momentum of the 3 masses must be zero. This essentially says this is a 2 DOF system.
Note: If we tried to find a flexibility matrix it is not defined.
We can write the constraint in a compound form as:
We can now solve the eigenvalue problem using
![]()
![]()
so that
![]()
For the example above set ![]() ,
, ![]()
![Rendered by QuickLaTeX.com \begin{equation*}[k']=\begin{bmatrix}1 & 0 & -1 \\0 & 1 & -1 \\\end{bmatrix}\begin{bmatrix}k & -k & 0 \\-k & 2k & -k \\0 & -k & k \\\end{bmatrix}\begin{bmatrix}1 & 0 \\0 & 1 \\-1 & -1 \\\end{bmatrix}=\begin{bmatrix}1 & 0 & -1 \\0 & 1 & -1 \\\end{bmatrix}\begin{bmatrix}k & -k \\0 & 3k \\-k & -2k \\\end{bmatrix}=\begin{bmatrix}2k & k \\k & 5k \\\end{bmatrix}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-612607e7fdea73e1081758218ca6ffb8_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}[m'] = m\begin{bmatrix}2 & 1 \\1 & 2 \\\end{bmatrix}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a8bbf07c128053db2ad0b217013ff6e9_l3.png)
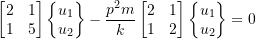
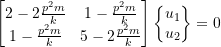
![]()
![]()
![]()
![]()
![]()
![]()
![]()

A second example of a 2DOF system is the vibration absorber as it can provide quite spectacular results when applied correctly. We will consider it first as a 2DOF undamped system, then include viscous damping. The closed form solution for the case of damping is much more involved.
Undamped Vibration Absorber

![]()
![]()
![]()
![]()
![]()
For S.S. solution, assume:
![]()
Under the steady state assumption, the equations of motion become:
![]()
![]()
Therefore, from ![]() :
:
![]()
And then from ![]() :
:
![]()
![]()
Therefore:
![]()
![]()
For use in vibration absorber applications, we define:
![]()
Then divide numerator and denominator by ![]() .
.
For the 2DOF system shown with the forcing appiled to the mass ![]() , the response of the masses
, the response of the masses ![]() and
and ![]() is:
is:
![]()
![]()
It is seen that from ![]() that if
that if ![]() or
or ![]() , then the mass
, then the mass ![]() is stationary. This leads to the idea that the motion of
is stationary. This leads to the idea that the motion of ![]() can theoretically be reduced to zero if we employ
can theoretically be reduced to zero if we employ ![]() ,
, ![]() at the operating frequency
at the operating frequency ![]() . For this application. the subsystem
. For this application. the subsystem ![]() ,
, ![]() is called a vibration absorber and at the operating frequency:
is called a vibration absorber and at the operating frequency:
![]()
For this application it is useful to modify ![]() and
and ![]() to reflect what we can call – the original system
to reflect what we can call – the original system ![]() ,
, ![]() , the absorber system
, the absorber system ![]() ,
, ![]() using the definitions:
using the definitions:
![]()
Using those definitions show that ![]() and
and ![]() become:
become:
![Rendered by QuickLaTeX.com \[X_1 = \frac{\frac{F_o}{k_1}\left[1-\left(\frac{\omega}{p_{22}}\right)^2\right]}{\left{\left[1-\left(\frac{\omega}{p_{22}}\right)^2\right]\left[1+\mu\left(\frac{p_{22}}{p_{11}}\right)^2-\left(\frac{\omega^2}{p_{11}}\right)^2\right] - \mu\left(\frac{p_{22}}{p_{11}}\right)^2\right}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3560b0bf3b50cdb0e152881b5ae2f268_l3.png)
![Rendered by QuickLaTeX.com \[X_2 = \frac{\frac{F_o}{k_1}}{\left{\left[1-\left(\frac{\omega}{p_{22}}\right)^2\right]\left[1+\mu\left(\frac{p_{22}}{p_{11}}\right)^2-\left(\frac{\omega^2}{p_{11}}\right)^2\right] - \mu\left(\frac{p_{22}}{p_{11}}\right)^2\right}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-895105d702afd5915b7c63c213c3359e_l3.png)
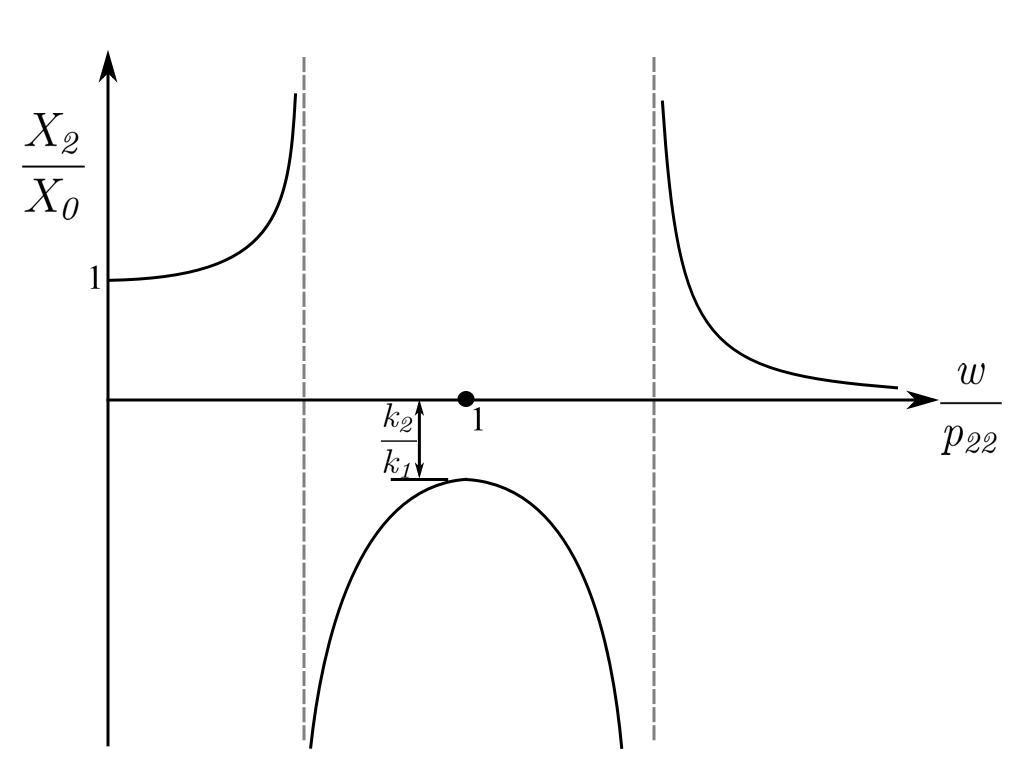
And when ![]() :
:
![]()
This shows that when the subsystem ![]() ,
, ![]() is timed so
is timed so ![]() that
that ![]() is motionless as the force in the spring
is motionless as the force in the spring ![]() exactly opposes the excitation force
exactly opposes the excitation force ![]() .
.

The natural frequencies of the combined system are found from setting the denominator of the responses ![]() ,
, ![]() to zero. Therefore, the natural frequencies are found when
to zero. Therefore, the natural frequencies are found when ![]() is replaced by
is replaced by ![]() and the expression becomes:
and the expression becomes:
![]()
![]()
Therefore:
![]()
![]()
If ![]() , this becomes:
, this becomes:
![]()
If instead of the mass ![]() being excited by the force
being excited by the force ![]() , the exication is through the base as
, the exication is through the base as ![]() , what is the difference in the response of
, what is the difference in the response of ![]() and
and ![]() of masses
of masses ![]() and
and ![]() ?
?
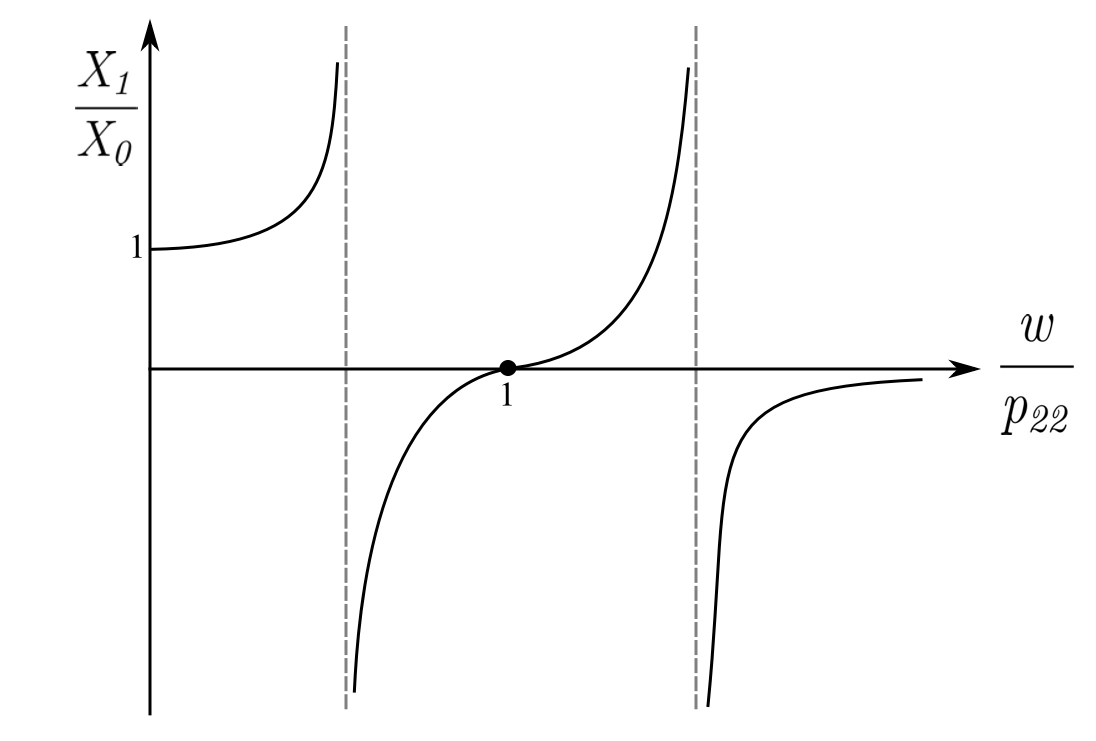
The mass ratio, ![]() , essentially determines the spread of the two resonances:
, essentially determines the spread of the two resonances:
![]()
![]()
![]()
(![]() )
)
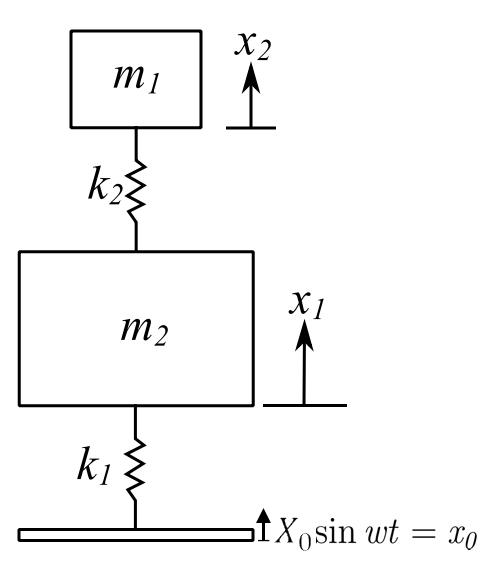
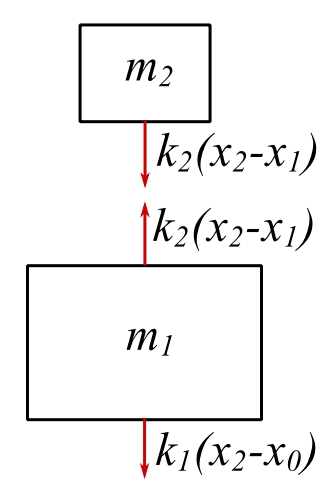
![]()
![]()
Therefore, the equations are identical except that ![]() is replaced by
is replaced by ![]() . The response of
. The response of ![]() and
and ![]() for the vibration absorber is:
for the vibration absorber is:
![]()
![]()
Again when ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\begin{split} X_2 &= -X_o\frac{1}{\mu}\Big(\frac{p_{11}}{p_{22}}\Big)^2 \\&= -X_o\frac{m_1}{m_2}\frac{k_1}{m_1}\frac{m_2}{k_2} \\&= -X_o\frac{k_1}{k_2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9963cf284867a8ccf0bb8f826b73a76e_l3.png)
Therefore, ![]() so that at any time:
so that at any time:
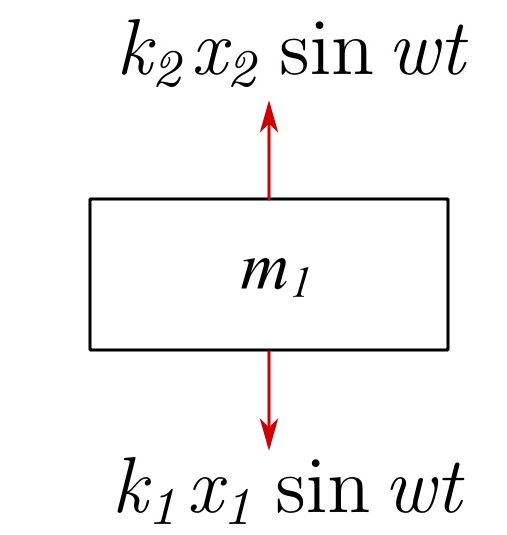
And the net dynamic force on ![]() is zero!
is zero!
To solve the system with damping it is more advantageous to use complex numbers:
![]()
Or:
![]()
There are a number of special cases of the general forced damped analysis that are useful.
Damped Forced 2DOF System
Consider a general damped system that can be specialized for special applications.
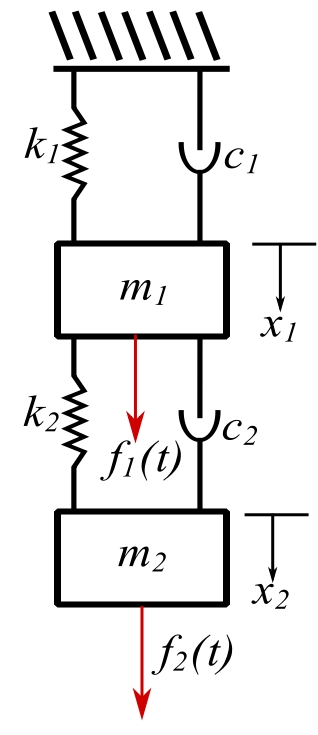

![]()
![]()
![]()
![]()
![]()
Assume a solution
![]()
Thus:
![]()
![]()
Therefore:
![]()
![]()
![]()
![]()
![]()
And we wish to find ![]() and
and ![]() :
:
![]()
![]()
![]()
Where ![]() . Thus:
. Thus:
![]()
![]()
There is a lot hidden in these symbols so we can consider some special cases.
1. Untuned Viscous Vibration Absorber
(Houdaille damper or viscous Lanchester damper)
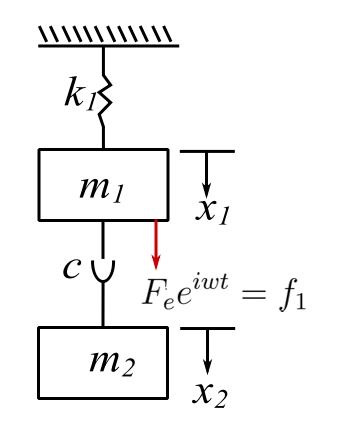
If we look at our general solution then:
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![]()
Put ![]() :
:
![]()
Therefore:
![]()
![]()
We are really interested in the amplitudes. Use the result that if:
![Rendered by QuickLaTeX.com \[\begin{split} \zeta &= \frac{B+iC}{D+iE} \cdot \frac{D-iE}{D-iE} \\&=\frac{BD+CE+i(CD-BE)}{D^2+E^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f47e78813f09a37aea146736b3d0cb11_l3.png)
We wish to write ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{split} A &= \frac{\sqrt{(BD+CE)^2 + (CD-BE)^2}}{D^2 + E^2} \\&= \frac{\sqrt{(BD)^2 + (CE)^2 + 2BDCE + (CD)^2 + (BE)^2 - 2BCDE}}{D^2+E^2} \\&= \frac{\sqrt{B^2(D^2+E^2) + C^2(D^2+E^2)}}{D^2+E^2} \\&= \sqrt{\frac{B^2+C^2}{D^2+E^2}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-46b910ff63a11c35cf3a097681cc3598_l3.png)
![]()
![]()
![]()
Thus:
![Rendered by QuickLaTeX.com \[ \frac{X_1}{X_o} = \frac{\sqrt{(\frac{m_2}{k}\omega^2)^2 + (\frac{c\omega}{k})^2}}{\sqrt{[\frac{m_2\omega^2}{k}(1-\frac{m_1\omega^2}{k})]^2 + (\frac{c\omega}{k})^2[\frac{m_2\omega^2}{k} - (1- \frac{m_1\omega^2}{k})]^2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-496816ceea6a640cbd1f1114ad999ccc_l3.png)
![]()
![]()
![]()
Thus:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{X_1}{X_o} &= \frac{\sqrt{\mu^2r^4 + (2\nu r)^2}}{\sqrt{[\mu r^2(1-r^2)]^2 + (2\nu r)^2[\mu r^2 - (1-r^2)]^2}} \\& = \frac{\sqrt{\mu^2r^2 + 4\nu ^2}}{\sqrt{[\mu r(1-r^2)]^2 + 4\nu ^2[\mu r^2 - (1-r^2)]^2}} \\&= \sqrt{\frac{N}{D}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-98c6a683033b268952ef45e81fad98e2_l3.png)
We wish to find the optimum ratio ![]() which minimizes this amplitude;
which minimizes this amplitude;
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\text{d}\frac{X_1}{X_o}}{\text{d}\nu} &= \frac{D^{\frac{1}{2}}\frac{N^{-\frac{1}{2}}}{2}(8\nu) - N^{\frac{1}{2}}\frac{D^{\frac{-1}{2}}}{2}(8\nu)[\mu r^2 - (1-r^2)]^2}{D} \\&= 0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5cee36945112a4f7f30656063ed4c275_l3.png)
Multiply by ![]() . Therefore:
. Therefore:
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![]()
Therefore, the minimum amplitude for optimum ![]() occurs when
occurs when ![]() . To find the value of
. To find the value of ![]() , use this value of
, use this value of ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{X_1}{X_o} &= \frac{\sqrt{\frac{\mu^2 2}{2+\mu} +4\nu^2}}{\sqrt{\frac{\mu^2 2}{2+\mu} (1- \frac{2}{2+\mu})^2 + 4\nu^2[\mu\frac{2}{2+\mu} - (1-\frac{2}{2+\mu})]^2}} \\&= \frac{\sqrt{\frac{2\mu^2}{2+\mu} + 4\nu^2}}{\sqrt{\frac{2\mu^2}{2+\mu}\frac{\mu^2}{(2+\mu)^2} + 4\nu^2[\frac{2\mu}{2+\mu} - (\frac{\mu}{2+\mu}) ]^2}} \\&= \frac{\sqrt{\frac{2\mu^2 + 4\nu(2+\mu)}{2+\mu}}}{\sqrt{\frac{2\mu^4}{(2+\mu)^3} + \frac{4\nu^2\mu^2}{(2+\mu)^2}}} \\&= \frac{\sqrt{2\mu^2 +4\nu^2(2+\mu)}}{\mu\sqrt{\frac{2\mu^2 + 4\nu^2(2+\mu)}{(2+\mu)^2}}} \\&= \frac{2+\mu}{\mu} = \frac{X_1}{X_o}\Big|_{\text{MAX}} \\&= 5\quad (\mu = \frac{1}{2}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3fb39c0762df0d92a4f9d53d15c48b96_l3.png)
The amplitude at this value of ![]() is independent of
is independent of ![]() !
!
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{X_1}{X_o} &= \frac{\sqrt{\mu^2r^2 + 4\nu^2}}{\sqrt{\mu^2r^2(1-2r^2+r^4)+4\nu^2[r^2(1+\mu)-1]^2}} \\&= \frac{\sqrt{\mu^2r^2 + 4\nu^2}}{\sqrt{\mu^2(r^2-2r^4+r^6) + 4\nu^2[r^4(1+\mu)^2-2r^2(1+\mu)+1]}} \\&= \sqrt{\frac{N}{D}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-005e385017dab6d2311e6d1ba92137a8_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\text{d}(\frac{X_1}{X_o})}{\text{d}r} &= \frac{D^{\frac{1}{2}}\frac{N^{-\frac{1}{2}}}{2}2\mu^2r-N^{\frac{1}{2}}\frac{D^{-\frac{1}{2}}}{2}[\mu^2(2r+8r^3+6r^5) + 4\nu^2(4r^3(1+\mu)^2 - 4r(1+\mu))]}{D} \\& = 0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-47c13702f1f70ed325ca0922c6738090_l3.png)
Multiply by ![]() . Then:
. Then:
![]()
Now evaluate this for ![]() .
.
![]()
Note that:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{X_1}{X_0} &= \sqrt{\frac{N}{D}} \\&= \frac{2+\mu}{\mu} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-676c2ba23783db73f362b758ac2bfd48_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
When ![]() :
:
![]()
When ![]() :
:
![Rendered by QuickLaTeX.com \[ \frac{X_1}{X_0} = \frac{\sqrt{ 0.25 + 4(0.365)^2}}{\sqrt{4(0.365)^2(\frac{1}{4})}} = 2.42\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cf20d71b1d945edc157340d92999d403_l3.png)
When ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{X_1}{X_0} = \frac{\sqrt{0.25 + 4}}{\sqrt{4(1)(\frac{1}{4})}} = 2.06\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-39f583f3f2167be53fa6e2ba224d8b8f_l3.png)
When ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{X_1}{X_0} = \frac{\sqrt{0.25 + 0.04}}{\sqrt{4(0.01)(\frac{1}{4})}} = 5.39\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bdc6171be98eddd86e6ec5e5bc7da263_l3.png)
When ![]() :
:
![]()
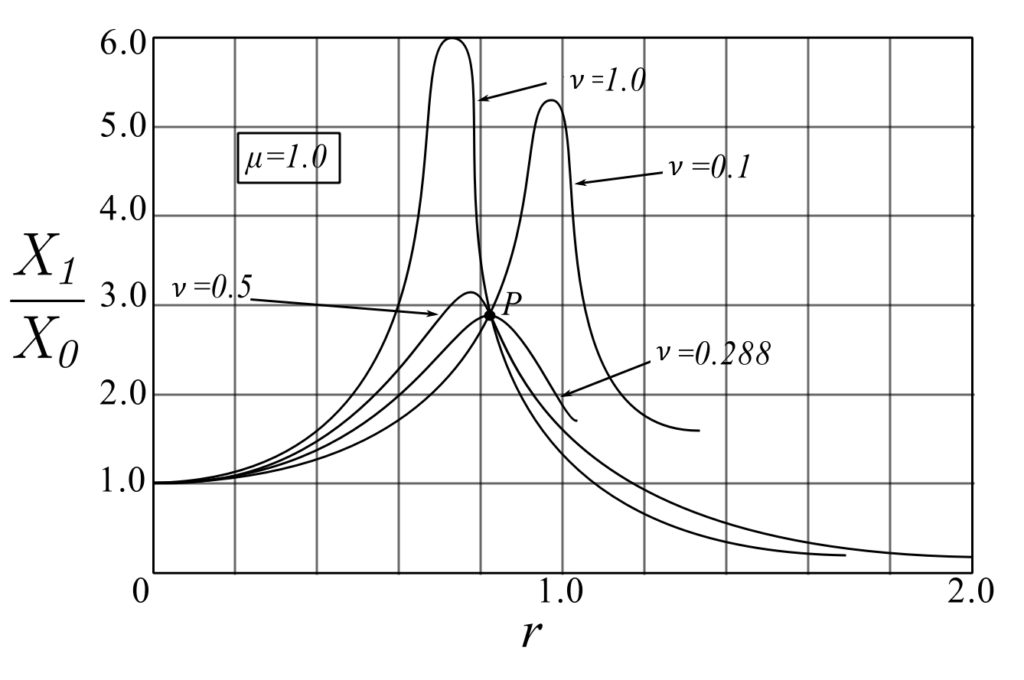
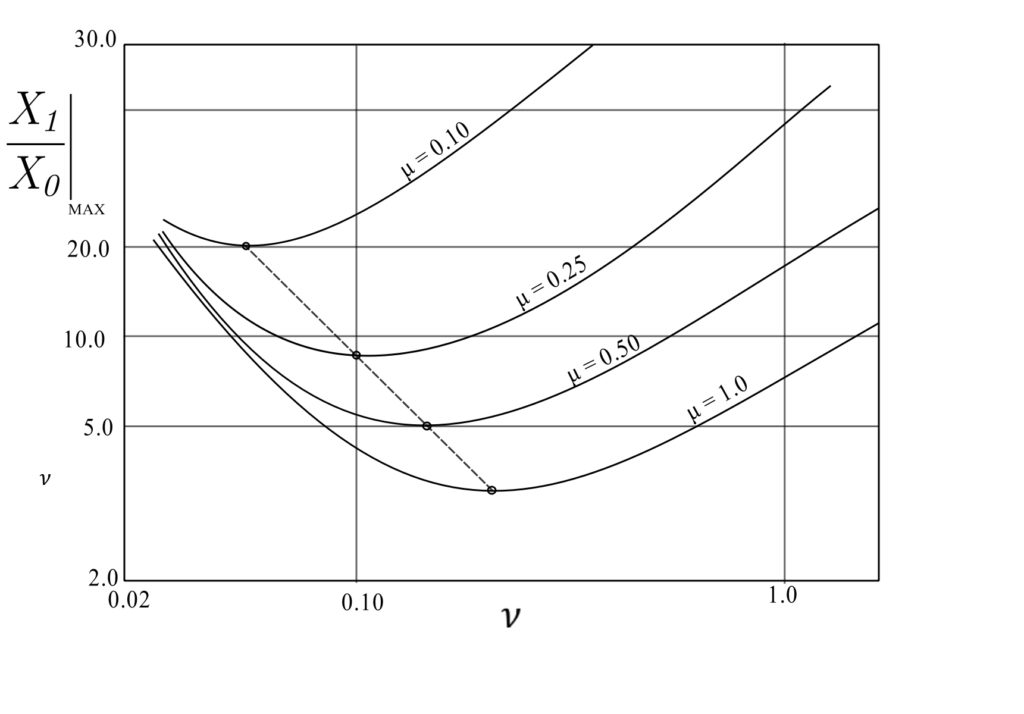
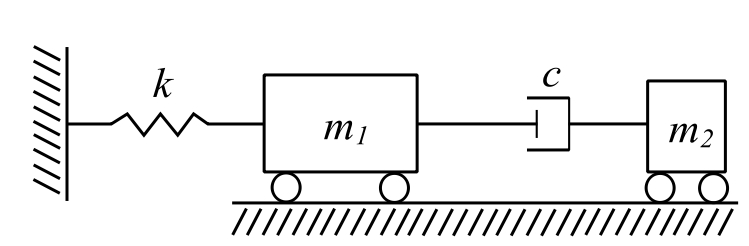
Example
A second very practical application is the viciously damped vibration absorber.
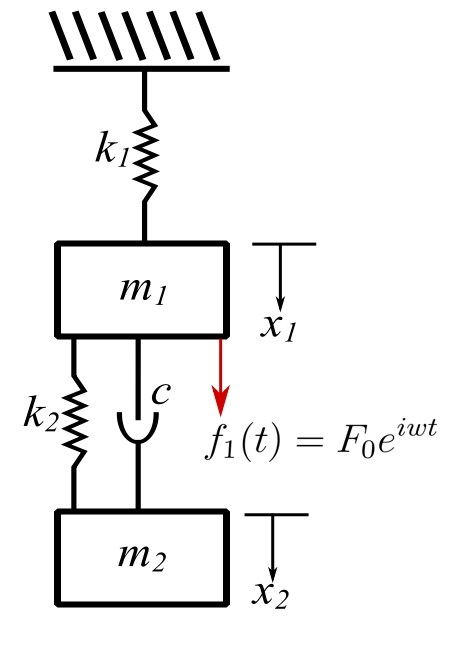
Solution
From the general solution:
![]()
Therefore:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If we set ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\begin{split}\zeta_2 &= Y_{21}f_1 \\&= \frac{k_2 + ic\omega}{\Delta \bar{\Delta}} \\&= X_2e^{i\theta_2} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5cff66251d2a6612779286818f2b5744_l3.png)
![]()
In order to apply this to various situations, it is useful to non-dimensionalize these relationships similar to that of the undamped vibration absorber.
Set:
![]()
![]()
NOTE:
![]()
![]()
Therefore:
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}(k_2 - m_2\omega^2)^2 &= k_1^2\bigg[\frac{k_2}{k_1} - \frac{m_2\omega^2}{k_1} \bigg] ^2 \\&= \bigg[\frac{m_1}{m_2}\frac{k_2}{k_1}\frac{m_2}{m_1} - \frac{m_2}{m_1}\omega^2 \frac{m_1}{k_1}\bigg]^2k_1^2 \\&= \mu^2k_1^2[r^2 - g^2]^2 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b71b9306baf1b150f09f78f6d6da0eb5_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}\Delta \bar{\Delta} &= \big[(-m_1\omega^2 + k_1)(-m_2\omega^2 + k_2) - m_2\omega^2 k_2 \big] ^2 + c^2\omega^2[-m_1\omega^2 + k_1 - m_2 \omega^2 \big] ^2 \\&= (2\nu r)^2[r^2 - 1 + \mu r^2]^2 + \big[\mu g^2r^2 - (r^2-1)(r^2-g^2)\big]^2\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6710b492fa252200ed4e47802591c006_l3.png)
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \frac{X_2}{X_0} = \frac{\mu r\sqrt{1+4\nu^2}}{\sqrt{(2\nu r)^2(r^2 - 1 +\mu r^2)^2 + \big[\mu g^2r^2 - ( r^2 - 1)(r^2 - g^2)\big]^2}}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-dda52f02de41658a31e1a2327086df97_l3.png)
CHECK
- If
 :
:![Rendered by QuickLaTeX.com \[\frac{X_1}{X_0} = \frac{r^2 - g^2}{\mu g^2r^2 - (r^2 - 1)(r^2 - g^2)} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-40d79fc1a7f220c16ef0f45c35167009_l3.png)
- If
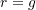 , then
, then 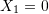
Note that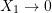 only when
only when 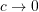
If :
:![Rendered by QuickLaTeX.com \[ \begin{split}\frac{X_1}{X_0} &= \frac{1}{r^2 - 1 + \mu r^2} \\&= \frac{1}{(1+\mu)r^2-1} \\&= \frac{1}{\frac{m_1 + m_2}{k_1}\omega^2 -1} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7f2358da89a26903bfad3a658f318a24_l3.png)
As a result somewhere between ![]() and
and ![]() ,
, ![]() will give an optimal result.
will give an optimal result.
Note that all the curves intersect at ![]() and
and ![]() . That is these points are independent of the damping. If we calculate their location, our problem is essentially solved as we must find the curve that passes through them with a horizontal tangent. Also by changing the “tuning”
. That is these points are independent of the damping. If we calculate their location, our problem is essentially solved as we must find the curve that passes through them with a horizontal tangent. Also by changing the “tuning” ![]() the two points can be shifted up and down the
the two points can be shifted up and down the ![]() curve. We can do this until the two points have the same height and the horizontal tangent through one of them.
curve. We can do this until the two points have the same height and the horizontal tangent through one of them.
To find the two points where the amplitude is independent of the damping ![]() and this is independent when
and this is independent when ![]() :
:
![]()
This leads to:
![]()
The negative gives ![]() while the positive gives
while the positive gives ![]() .
.
The two answers for the forcing frequency ratio are functions of ![]() and
and ![]() but not of the damping
but not of the damping ![]() .
.
We now wish to adjust ![]() so that
so that ![]() &
& ![]() are equal. Since their magnitude is independent of the damping, choose
are equal. Since their magnitude is independent of the damping, choose ![]() then the magnitude:
then the magnitude:
![]()
For ![]() and
and ![]() (the two roots), we want the same magnitude:
(the two roots), we want the same magnitude:
![]()
Therefore:
![]()
![]()
Now it is not necessary to solve for ![]() and
and ![]() if we remember the sum of the roots in a quadratic in the negative coefficient of the middle term.
if we remember the sum of the roots in a quadratic in the negative coefficient of the middle term.
Therefore:
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} \implies g^2(1+\mu) &= \frac{2+\mu - 1 - \omega}{1+ \mu} \\&= \frac{1}{1+\mu} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f17f55c2efdd5ae4b19f6548b578065c_l3.png)
Therefore:
![]()

Amplitudes of the main mass for various values of absorber damping. The absorber is twenty times as small as the main machine and is tuned to the same frequency. All curves pass through the fixed points ![]() and
and ![]() .
.
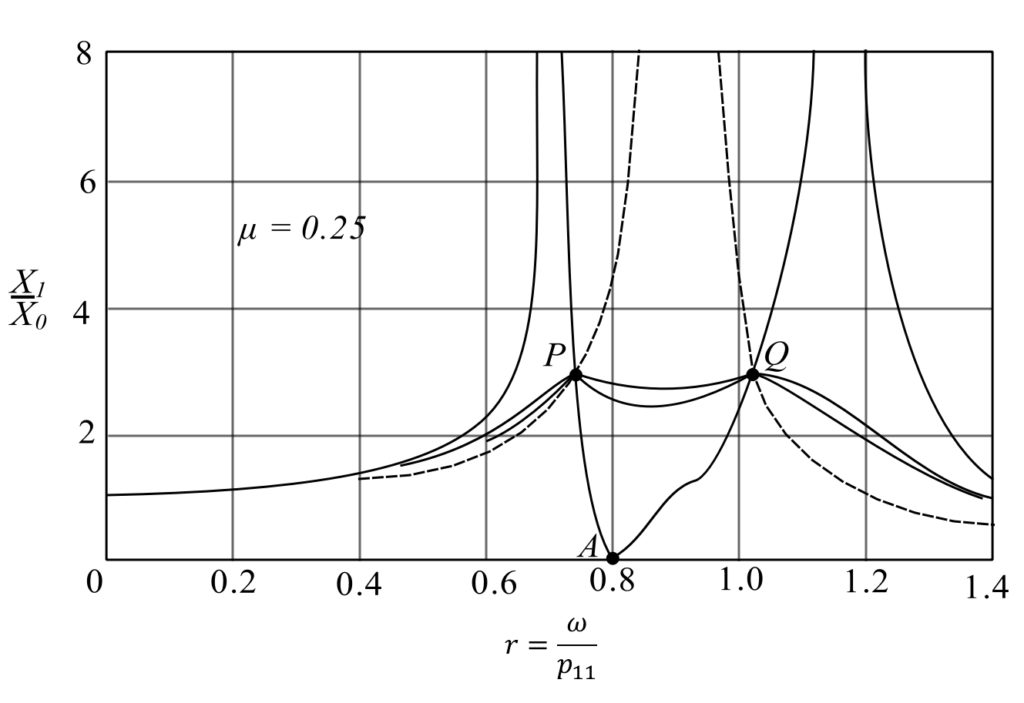
Resonance curves for the motion of the main mass fitted with the most favorably tuned vibration-absorber system of one-forth of the size of the main machine.
(a)
(b)
(c)
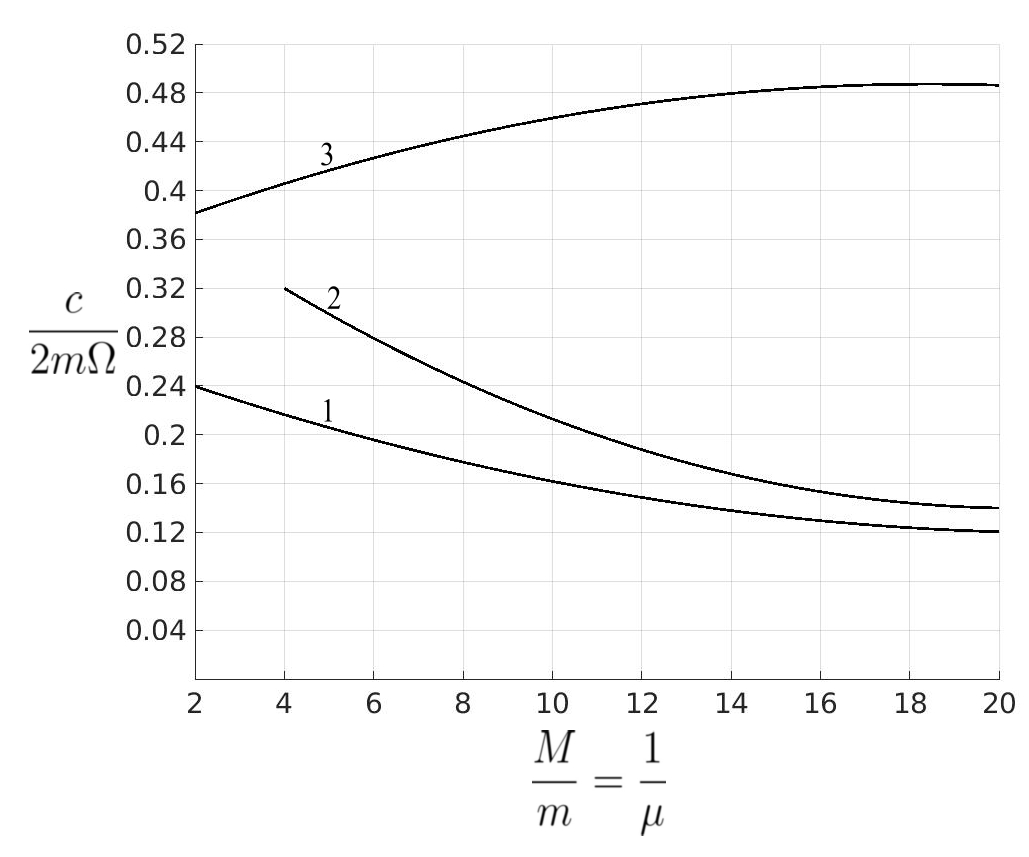
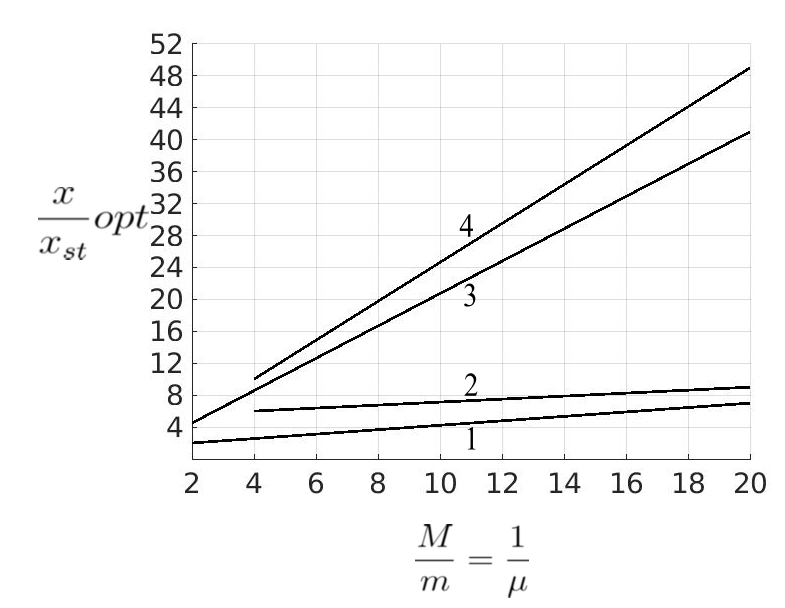
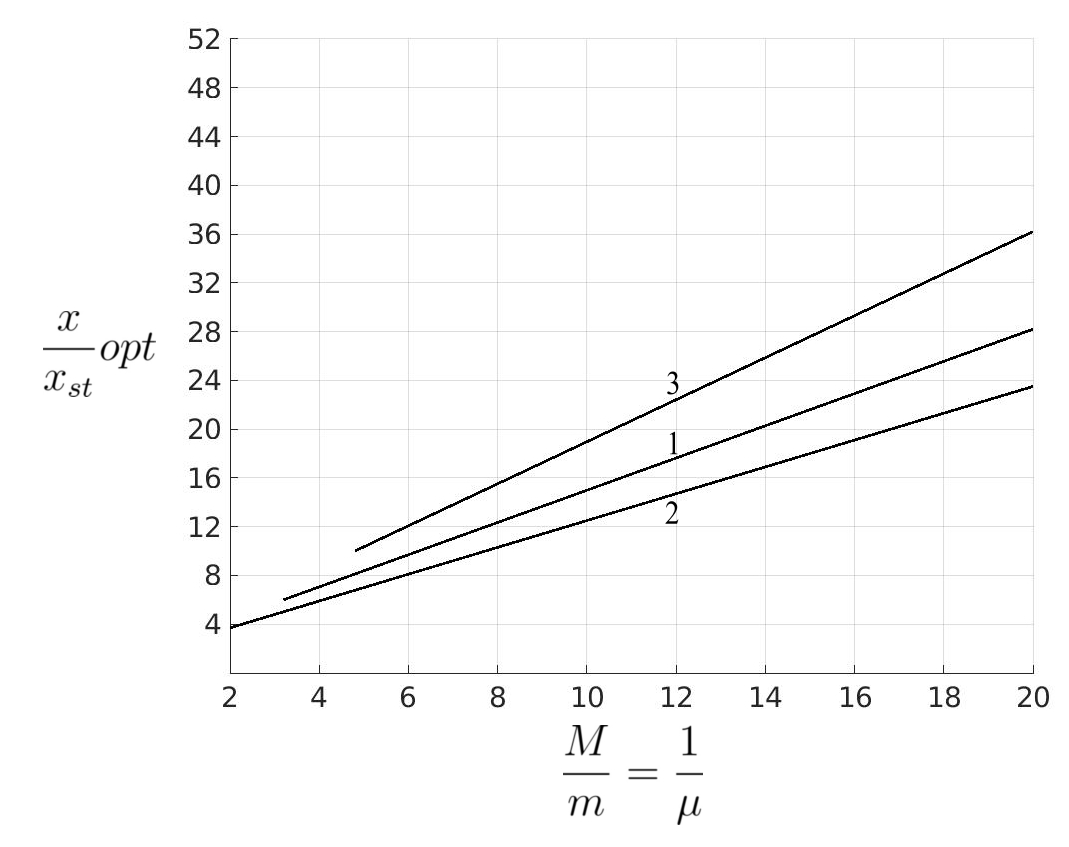
(a) Peak amplitudes of the main mass as a function of the ratio ![]() for various absorbers attached to the main mass. (b) Peak relative amplitudes between the masses
for various absorbers attached to the main mass. (b) Peak relative amplitudes between the masses ![]() and
and ![]() for various absorbers. (c) Damping constants required for the most favorable operation of the absorber,
for various absorbers. (c) Damping constants required for the most favorable operation of the absorber, ![]() , for obtaining the results of (a) and (b).
, for obtaining the results of (a) and (b).
Curve 1 for the most favorably tuned and damped absorber; curve 2 for the most favorably damped absorber tuned to the frequency of the main system; curve 3 of the most favorably damped viscous Lanchester damper; curve 4 for the most favorably damped Coulomb Lanchester damper.
![]()
and using one of the roots:
![]()
while the optimum damping is given by:
![]()

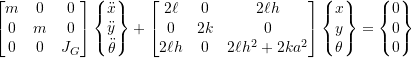
![Rendered by QuickLaTeX.com \begin{equation*}[m]=\begin{bmatrix}m_1 & 0 & 0 \\0 & m_2 & 0 \\0 & 0 & m_3 \\\end{bmatrix}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9b12243663d135c70ed2f7ab57d46beb_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}[k]=\begin{bmatrix}k_1 & -k_1 & 0 \\-k_1 & k_1+ k_2 & -k_2 \\0 & -k_2 & k_2 \\\end{bmatrix}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6928e0ee7372be20d807a5960f1f9db2_l3.png)
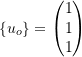
![Rendered by QuickLaTeX.com \begin{equation*} [k] \{u\}= \begin{bmatrix} k_1 & -k_1 & 0 \\ -k_1 & k_1+ k_2 & -k_2 \\ 0 & -k_2 & k_2 \\ \end{bmatrix} \begin{bmatrix} 1\\ 1\\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix} =\{u\}^{T}[k] \end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3ef5196621616e2658406df5cec37418_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\{u\}^{T}[m]\begin{Bmatrix}\ddot{x}_1\\\ddot{x}_2\\\ddot{x}_3\\\end{Bmatrix}=0\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1de668bf4449e7ceab0765ed1a66aa6e_l3.png)
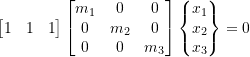
![Rendered by QuickLaTeX.com \begin{equation*}\begin{Bmatrix}x_1\\x_2\\x_3\\\end{Bmatrix}=\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\\frac{-m_1}{m_3} & \frac{-m_2}{m_3} & 0 \\\end{bmatrix}\begin{Bmatrix}x_1\\x_2\\x_3\\\end{Bmatrix}=\begin{bmatrix}1 & 0 \\0 & 1 \\\frac{-m_1}{m_3} & \frac{-m_2}{m_3} \\\end{bmatrix}\begin{Bmatrix}x_1\\x_2\\\end{Bmatrix}=[C]\begin{Bmatrix}x_1\\x_2\\\end{Bmatrix}\end{equation*}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fad8a549a29c28edff8da1ee224b6e2c_l3.png)