Review of single and multi-degree of freedom (mdof) systems: Complex Representation for Vibrations
When dealing with vibrating equations it is often more efficient to use complex numbers as they allow the phase relationships to be easily handled. To do this use the complex number:
![]()
![]()
![]() is called the complex conjugate
is called the complex conjugate

![]()
Alternatively we write ![]() as:
as:
![]()
![]() is called a unit phasor. For fractional expressions we can rationalize the denominator to separate real & imaginary parts:
is called a unit phasor. For fractional expressions we can rationalize the denominator to separate real & imaginary parts:
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} C &= \frac{a + i\alpha}{b+i\beta} \frac{b- i\beta}{b- i\beta} \\&= \frac{(ab+\alpha \beta ) + i(\alpha b - a \beta)}{b^2 + \beta ^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fb3939b74b9d558b84b7694209e8078c_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} C^\star &= \frac{a - i\alpha}{b-i\beta} \frac{b+ i\beta}{b+ i\beta} \\&= \frac{(ab+\alpha \beta ) - i(\alpha b - a \beta)}{b^2 + \beta ^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-71b8ab3bc66d2016a75db65a352a4daf_l3.png)
Consider the steady-state forced SDOF system:
![]()
![]()
and we want to imaginary part of the solution
Try ![]() , where
, where ![]() is complex, therefore:
is complex, therefore:
![]()
![]()
Note: ![]() ,
, ![]() is defined as the mechanical impedence.
is defined as the mechanical impedence.
Rationalizing the denominator gives:
![Rendered by QuickLaTeX.com \[ \begin{split} \tilde{X} &= \frac{F_o [(k - m \omega ^2) - ic \omega]}{[(k - m \omega ^2) +(c \omega )^2]} \\& \equiv Xe^{-i \phi} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-dade4481aa6aa284020ae7f06ec5f311_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} X &= |\tilde{X}| \\&=\frac{F_o}{\sqrt{(k-m \omega ^2)^2 + (c \omega)^2}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f7b1acfe94bbe8af54de42d1ee6628d7_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} \tilde{x} &=\frac{F_o}{\sqrt{(k-m \omega ^2)^2 + (c \omega)^2}} e\strut^{-i\phi} e\strut^{i \omega t} \\ &= Xe\strut^{i(\omega t - \phi)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5aad72d216c474e58b80115bada77e91_l3.png)
as ![]()
Then the imaginary part of the solution is:
![]()
We can now re-interpret equation ![]() as:
as:
![]()
![]()
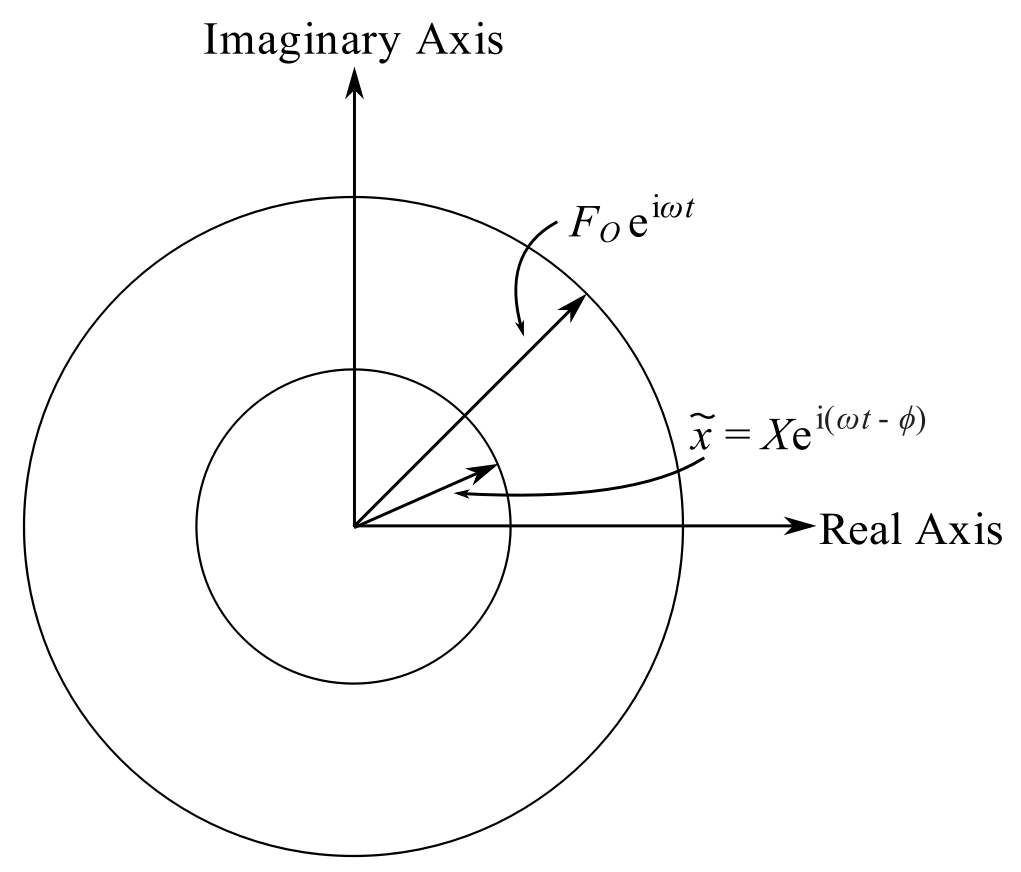
Each of the force terms above can be interpreted in their respective phases.
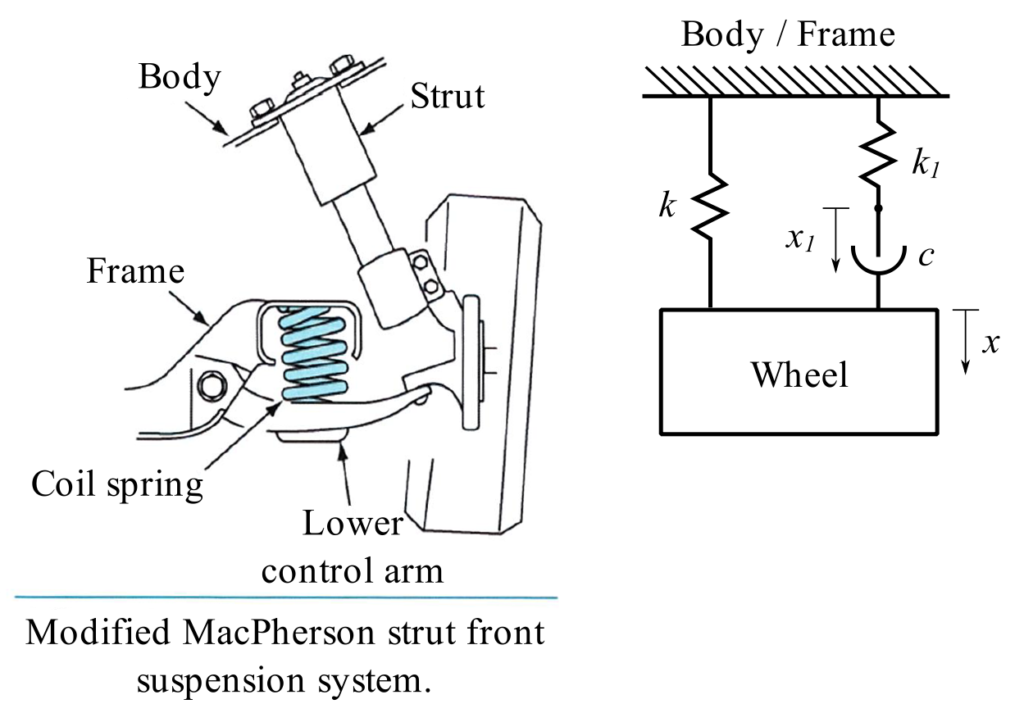
Many real automotive suspension systems use the so-called Macpherson strut which is a combined spring and damper along with a coil spring as shown in the diagram. The system can be represented by the diagram where the forcing function comes from road surface. (This system is sometimes called a 1 & ![]() DOF system).
DOF system).
a) Using the mechanical impedance find that the displacement ![]() and
and ![]() .
.
b) For the model shown, determine the transmissibility of the system.
c) For the frequency ratio ![]() , and for
, and for ![]() . Calculate for the transmissibility and compare the values to the case in which
. Calculate for the transmissibility and compare the values to the case in which ![]() .
.
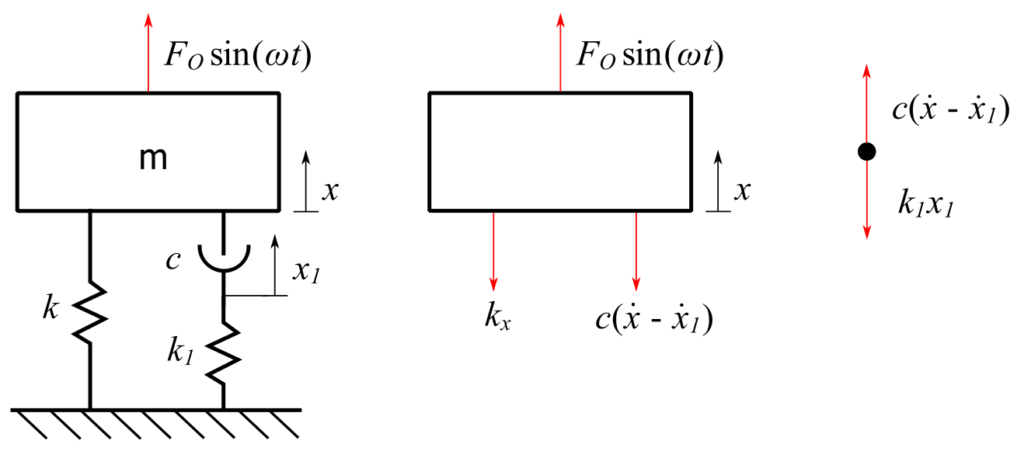
a)
![]()
![]()
Using ![]()
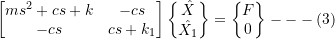
![]()
(3) is of the form:

Therefore:
![]()
![]()
If ![]() :
:
![]()
![]()
![]()
![]() , if
, if ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\hat{\Delta}}{kk_1} &= \biggr[(1- r^2) + i2\zeta r\Big(1+\frac{1}{N} - \frac{r^2}{N}\Big)\biggr] \\&= \biggr[(1- r^2)^2 + \Big\{ 2\zeta r\Big(1+\frac{1}{N} - \frac{r^2}{N}\Big) \Big\}\strut^2\biggr]\strut^\frac{1}{2} e\strut^{i\gamma} \\&= \hat{\Delta}e\strut^{i\gamma} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ef8be54b3728d76a62178d104c8ad973_l3.png)
![]()
If we set ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{split} \hat{X} &= \frac{F(1+\frac{i2\zeta r}{N})}{k \Delta e\strut^{i\gamma}} \\ &= \frac{F \sqrt{(1+\frac{2\zeta r}{N})}e\strut^{i\beta}}{k \Delta e\strut^{i\gamma}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-494db35c245bc69f8fb5f3051fdda93a_l3.png)
![]()
Therefore,
![]()
Where ![]()
![]()
Where ![]()
b) The force transmitted is
![Rendered by QuickLaTeX.com \[ \begin{split} F_T &= k \hat{X} + k_1 \hat{X_1} \\ &= F \frac{[k(k_1+ic \omega ) + k_1(ic \omega )]}{\hat{\Delta}} \\&= kk_1 F \frac{[1 + \frac{ic\omega }{k} + \frac{ic\omega }{k_1}]}{\hat{\Delta}}\\&= F \frac{[1+ i(2 \zeta r + \frac{2\zeta r)}{N}]}{\hat{\Delta}e\strut^{i\gamma}} \\&= F \sqrt {1+ \big[2\zeta r\big(1+ \frac{1}{N}\big)\big]\strut^2} \frac{e\strut^{-i\alpha _2}}{\hat{\Delta}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3d93db365b9bc67202077bbd7ff63eb3_l3.png)
![]()
c) For the case ![]() :
:
![]()
![]()
For the case ![]() :
:
![]()
![]()
The added spring ![]() reduces the transmissivity in both cases, however it is most effective at higher
reduces the transmissivity in both cases, however it is most effective at higher ![]() ratio.
ratio.
![Rendered by QuickLaTeX.com \[ \left| \frac{F_T}{F} \right| = \frac{\big[1+\{2\zeta r (1+ \frac{1}{N})\}^2\big]\strut^{1/2}}{\big[(1-r^2)^2+\{2\zeta r(1+\frac{1}{N} - \frac{r^2}{N}\}^2\big]\strut^{1/2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d1cd721cbf3a2d4fec75bfd2517c2100_l3.png)
If ![]()
![Rendered by QuickLaTeX.com \[ \left| \frac{F_T}{F} \right| = \frac{\big[1+(2 \zeta r)^2\big]\strut^{1/2}}{\big[(1-r^2)^2+(2\zeta r)^2\big]\strut^{1/2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a2a51c7432c957ee4ecdaccb56f0e6c6_l3.png)

![]()
![Rendered by QuickLaTeX.com \[ \left| \frac{F_T}{F} \right| = \frac{\big[1+\{2(0.4)(0.6)\frac{3}{2}\}^2\big]\strut^{1/2}}{\big[(1-0.36)^2+\{2(0.4)(0.6)(1+\frac{1}{2} - 0.18)\}^2\big]\strut^{1/2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6cebd3fdbe57b26c44d9359207c29f2a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \left| \frac{F_T}{F} \right| = \frac{\big[1+\{2(0.4)(10)\frac{3}{2}\}^2\big]\strut^{1/2}}{\big[(1-10^2)^2+\{2(0.4)(10)(\frac{3}{2} - \frac{100}{2})\}^2\big]\strut^{1/2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2df671ac3fe73134549349bba2f88ace_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ \frac{|F_T|}{F}\Bigg|_{k \rightarrow \infty} = \frac{\big[1+\{2(0.4)(10)\}^2\big]\strut^{1/2}}{\big[(1-10^2)^2+\{2(0.4)(10)\}^2\big]\strut^{1/2}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0f63abcb8196336c9b4cb882607f49b0_l3.png)
![]()
![]()
Extra Details
![Rendered by QuickLaTeX.com \[ \begin{split} \hat{\Delta} &= (ms^2 + cs + k)(cs + k_1) - c^2s^2 \\ &= cs(ms^2+k+k_1)+c^2s^2+k_1(k+ms^2)-c^2s^2 \\ &= cs(ms^2+k+k_1) + k_1(k+ms^2) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7dc3a93462ab2834e395269a97f69e79_l3.png)
If ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\hat{\Delta}}{kk_1} &= \Big[1 - \frac{\omega^2m}{k}\Big] + \frac{ic\omega}{k}\Big[\frac{-m\omega^2}{k_1} + 1 + \frac{k}{k_1}\Big] \\ &= \Big[1 - \frac{\omega^2}{p^2}\Big] + \frac{ic\omega m}{k}\Big[1 + \frac{1}{N} - \frac{r^2}{N}\Big] \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-545e6731bd6da4a77bab7cba388f0ab4_l3.png)
Where ![]() ,
, ![]() , and
, and ![]() . Thus:
. Thus:
![Rendered by QuickLaTeX.com \[ \begin{split} &= [1-r^2] + i2\zeta r\Big[1 + \frac{1}{N} - \frac{r^2}{N}\Big] \\ &= \biggr\{[1-r^2]^2 + \Big(2\zeta r\Big(1 + \frac{1}{N} - \frac{r^2}{N}\Big)\Big)^2\biggr\}\strut^{\frac{1}{2}}e\strut^{i\gamma} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8bf5fe117f7505f2355ca5720620e9e0_l3.png)
Where:
![]()
If ![]() ,
, ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} X &= \frac{\frac{F}{k}(1+\frac{2i\zeta r}{N})}{\Delta e^{i\zeta}} \\ &= \frac{\frac{F}{k}\sqrt{1 + (\frac{2\zeta r}{N})^2}}{\Delta e^{i\zeta}}e^{i\beta} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-abe507540cf6712005fbf068ba57e6b6_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} X_1 &= \frac{ic\omega F}{\hat{\Delta}} \\&= \frac{2\zeta r}{N \hat{\Delta}} e ^{i\frac{\pi}{2}} \\&=\frac{F}{k\Delta}\frac{2\zeta r}{N}e^{-i(\gamma-\frac{\pi}{2})}\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2e79eb325045159ff35b5961d3a4b561_l3.png)
