Advanced Dynamics and Vibrations: Numerical methods for vibrating systems
[Jason’s part goes here] ![]()
where we can have a different mass as the equation is different. For SHM
![]()
If we choose ![]() then
then
![]()
![]()
Therefore:
![]()
Note: ![]()
If ![]()
![Rendered by QuickLaTeX.com \[ \begin{split} \beta N &= \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2} \\ &= \frac{(2i-1)\pi}{2} \qquad i = 1,2,3, … \\ \frac{\beta}{2} &= \frac{(2i-1)\pi}{4N} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-27998bd88e967a1008927ccf93ba9d2b_l3.png)
Now using the result above
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{mp^2}{k} &= 4\sin^2\frac{\beta}{2} \\ p &= 2\sqrt{\frac{k}{m}}\sin\frac{\beta}{2} \\ p_i &= 2\sqrt{\frac{k}{m}}\sin\frac{(2i-1)\pi}{4N} \qquad i=1\rightarrow N \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8c43f39b58913795abe48fa712c6768f_l3.png)
Consider ![]()
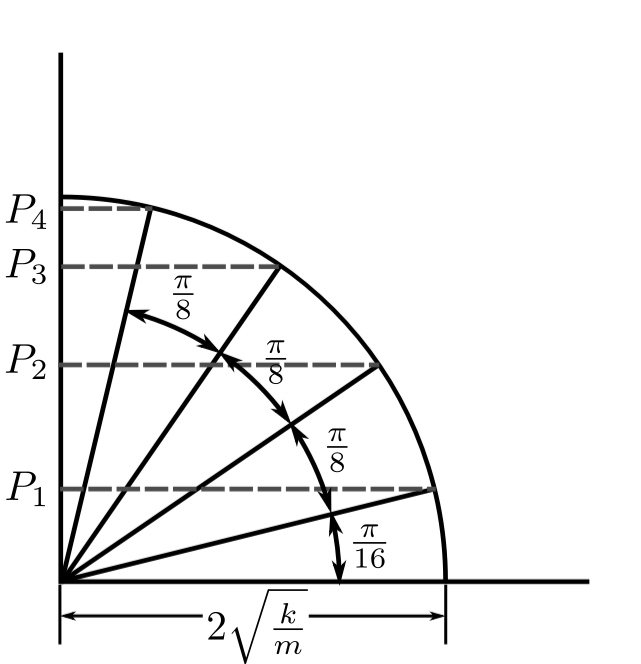
![Rendered by QuickLaTeX.com \[ \begin{split} p_1 &= 2\sqrt{\frac{k}{m}}\sin\frac{\pi}{16} = 0.390\sqrt{\frac{k}{m}} \qquad (11.25^{\circ}) \\ p_2 &= 2\sqrt{\frac{k}{m}}\sin\frac{3\pi}{16} = 1.11\sqrt{\frac{k}{m}} \qquad (33.75^{\circ}) \\ p_3 &= 2\sqrt{\frac{k}{m}}\sin\frac{5\pi}{16} = 1.66\sqrt{\frac{k}{m}} \qquad (56.25^{\circ}) \\ p_4 &= 2\sqrt{\frac{k}{m}}\sin\frac{7\pi}{16} = 1.96\sqrt{\frac{k}{m}} \qquad (78.75^{\circ}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-73813a758a4ca03d6b7d0b573dfff121_l3.png)
Note:
![Rendered by QuickLaTeX.com \[ \begin{split} p_5 &= 2\sqrt{\frac{k}{m}}\sin\frac{9\pi}{16} \\ &= 2\sqrt{\frac{k}{m}} \sin\Big(\frac{\pi}{2} + \frac{\pi}{16} \Big) \\ &= 2\sqrt{\frac{k}{m}}\Big(\sin\frac{\pi}{2}\sin\frac{\pi}{16} + \cos\frac{\pi}{2}\cos\frac{\pi}{16} \Big) = p_1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-903f44a23cd061f4b59d98c2823d00d9_l3.png)
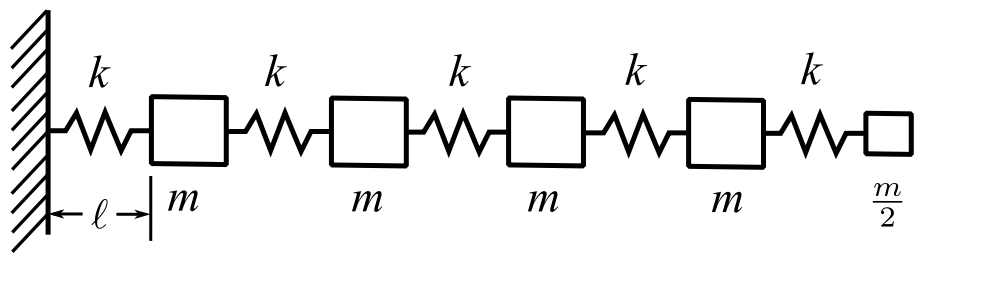
We can apply this idea to various dynamical systems which are more complicated than the simple spring/mass. Consider an approximation to longitudinal vibration of a bar

Consider a beam of total mass ![]() and cross section
and cross section ![]() modulus
modulus ![]() which we approximate as
which we approximate as
![]()
if ![]() , go to
, go to ![]()
if ![]()
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} \beta\sin\beta (N-1) &= \beta\sin\beta N\big(1-4\sin^2\frac{\beta}{2}\big) \\ \sin\beta(N-1) &= \sin\beta N\big[ 1-(2-2\cos\beta)\big] \\ \sin\beta(N-1) &= \sin\beta N [-1+2\cos\beta] \\ \sin\beta N\cos\beta - \cos\beta N\sin\beta &= 2\cos\beta\sin\beta N - \sin\beta N \\ -\cos\beta\sin\beta N - \cos\beta N\sin\beta &= \sin\beta N \\ -\big[ \cos\beta\sin\beta N + \cos\beta N \sin\beta\big] &= \sin\beta N \\ -\sin\beta(N+1) &= \sin\beta N \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-17c456ca3f197ae1c32d2ac81c3f625c_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\sin\beta(N-1)}{\sin\beta N} &= 1-4\sin^2\frac{\beta}{2} \\ 4\sin^2\frac{\beta}{2} &= 1 - \frac{\sin\beta(N-1)}{\sin\beta N} \\ 4\sin^2\frac{\beta}{2} &= \frac{\sin\beta N - \sin\beta (N-1)}{\sin\beta N} \\ \sin\frac{\beta}{2} &= \frac{\cos{\beta(N-\frac{1}{2}}}{\sin\beta N} \\ 2\sin\frac{\beta}{2}\sin\beta N &= \cos\beta(N-\frac{1}{2}) \\ 2\sin\frac{\beta}{2}\sin\beta N &= \cos\beta N\cos\frac{\beta}{2} + \sin\beta N\sin\frac{\beta}{2} \\ \sin\frac{\beta}{2}\sin\beta N - \cos\beta N \cos\frac{\beta}{2} &= 0 \\ \cos\beta(N+\frac{1}{2}) &= 0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7e75f1862b2b5b249d5fae6399188382_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} \beta(N+\frac{1}{2}) &= (2i-1)\frac{\pi}{2} \\ \beta &= \frac{2(2i+1)}{(2N+1)}\frac{\pi}{2} \\ &= \frac{(2i-1)\pi}{(2N+1)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c162565dd595f0da2f80116e270064f5_l3.png)
Therefore:
![]()
N = 4
![Rendered by QuickLaTeX.com \[ \begin{split} p_1 &= 2\sqrt{\frac{k}{m}} \sin{\frac{\pi}{18}} = 0.347\sqrt{\frac{k}{m}} \\ p_2 &= 2\sqrt{\frac{k}{m}} \sin{\frac{3\pi}{18}} = \sqrt{\frac{k}{m}} \\ p_3 &= 2\sqrt{\frac{k}{m}} \sin{\frac{5\pi}{18}} = 1.53\sqrt{\frac{k}{m}} \\ p_4 &= 2\sqrt{\frac{k}{m}} \sin{\frac{7\pi}{18}} = 1.88\sqrt{\frac{k}{m}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-058c5a1c489fa62933b9407154e25e1e_l3.png)
To calculate the mode shapes one can start at the free end e.g.:
![]()
Assume ![]()
![]()
Now we use the recursion relationship
![]()
Therefore:
![]()
For the 4 storey building for the lowest natural frequency is
![]()
Therefore:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} X_1 &= 2\cos11.25^{\circ}(0.92) \\ &= 2(\cos22.5^{\circ})^3 - \cos22.5^{\circ} \\ &= \underline{0.383} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-60b674f9989837b60c0089e770ef58bc_l3.png)
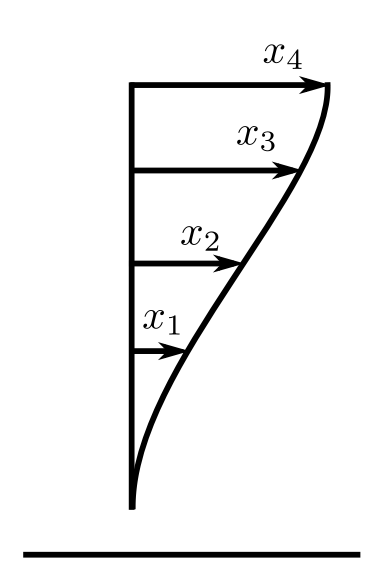
Check
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![]()
if ![]() (
(![]() is low) then:
is low) then:
![]()
for the lower frequencies
![]()
![Rendered by QuickLaTeX.com \[ \begin{split} p_i &= 2\sqrt{\frac{AEN^2}{ML}}\frac{(2i-1)\pi}{4N} \\ &= \frac{\pi(2i-1)}{2L} \sqrt{\frac{EAL}{M}} \\ &= \frac{\pi(2i-1)}{2L}\sqrt{\frac{E}{\rho}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e7b7a04a722e24144ab275a0d54b9779_l3.png)
where ![]() is density
is density
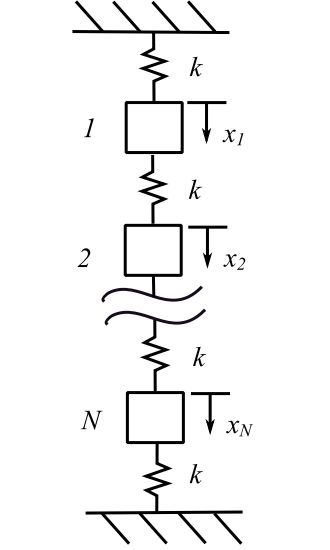
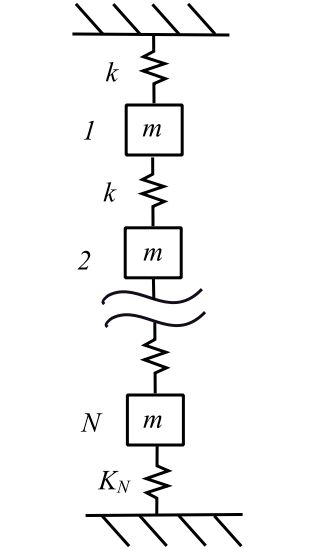
For other boundary conditions, the expression for ![]() is determined then the natural frequencies are known. For fixed ends.
is determined then the natural frequencies are known. For fixed ends.
![]()
![]()
Consider the fixed boundaries:
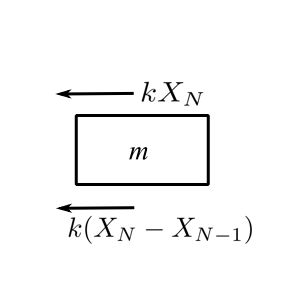
![Rendered by QuickLaTeX.com \[\begin{split}\rightarrow\sum F_x &= m\ddot{X}_n \\&= -mp^2X_N \\&= -kX_N - k(X_N-X_{N-1})\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d23162aaddb27e0b197862c7b0384bae_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![]()
![]()
![]()
Therefore:
![]()
Example
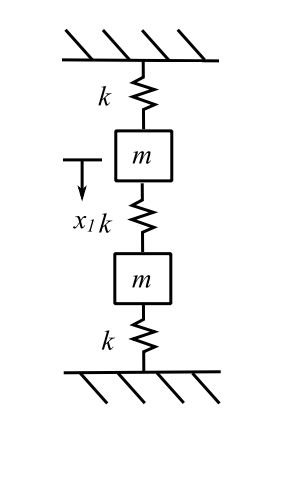
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split}p_1 &= 2\sqrt{\frac{k}{m}}\sin\frac{\pi}{6} \\&=\sqrt{\frac{k}{m}}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2454f7a4c07eec58aab1e43369e06aac_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}p_2 &= 2\sqrt{\frac{k}{m}}\sin\frac{2\pi}{6} \\&=\sqrt{\frac{3k}{m}}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0ae0681ba314b3b93652b83120bdaa3d_l3.png)
