Review of single and multi-degree of freedom (mdof) systems: Transient Vibrations
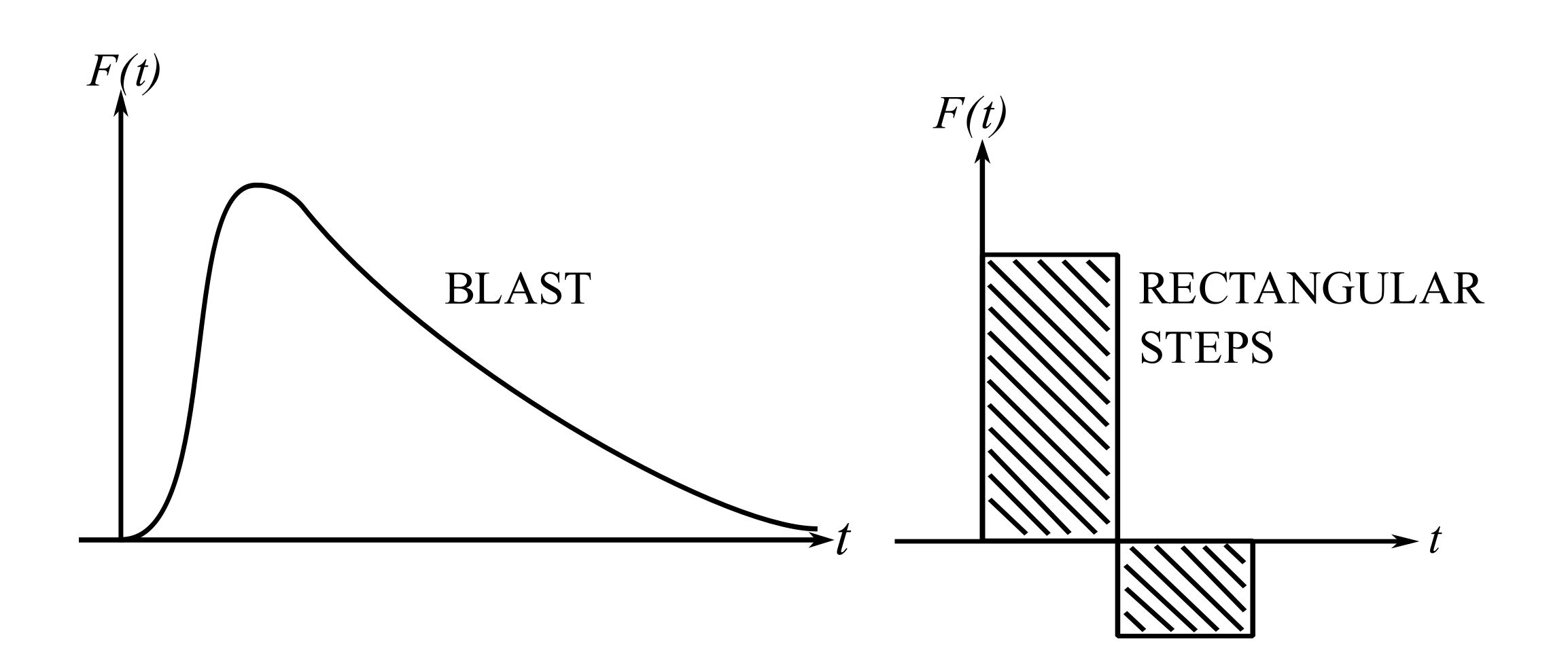
For dynamical systems excited by non-periodic forces, displacements, accelerations, etc., the response over the initial few periods of the system is termed transient response. This is important for many diverse situations including packaging of equipment, protecting people from automobile impacts, and loading of structures due to blasts and earthquakes. The modeling of these situations is often difficult and may require specific detail of the excitation as the response can vary dramatically depending on the detail of the input.
For a SDOF system the solution requires the general solution of ![]() and becomes difficult for complicated
and becomes difficult for complicated ![]()
Example
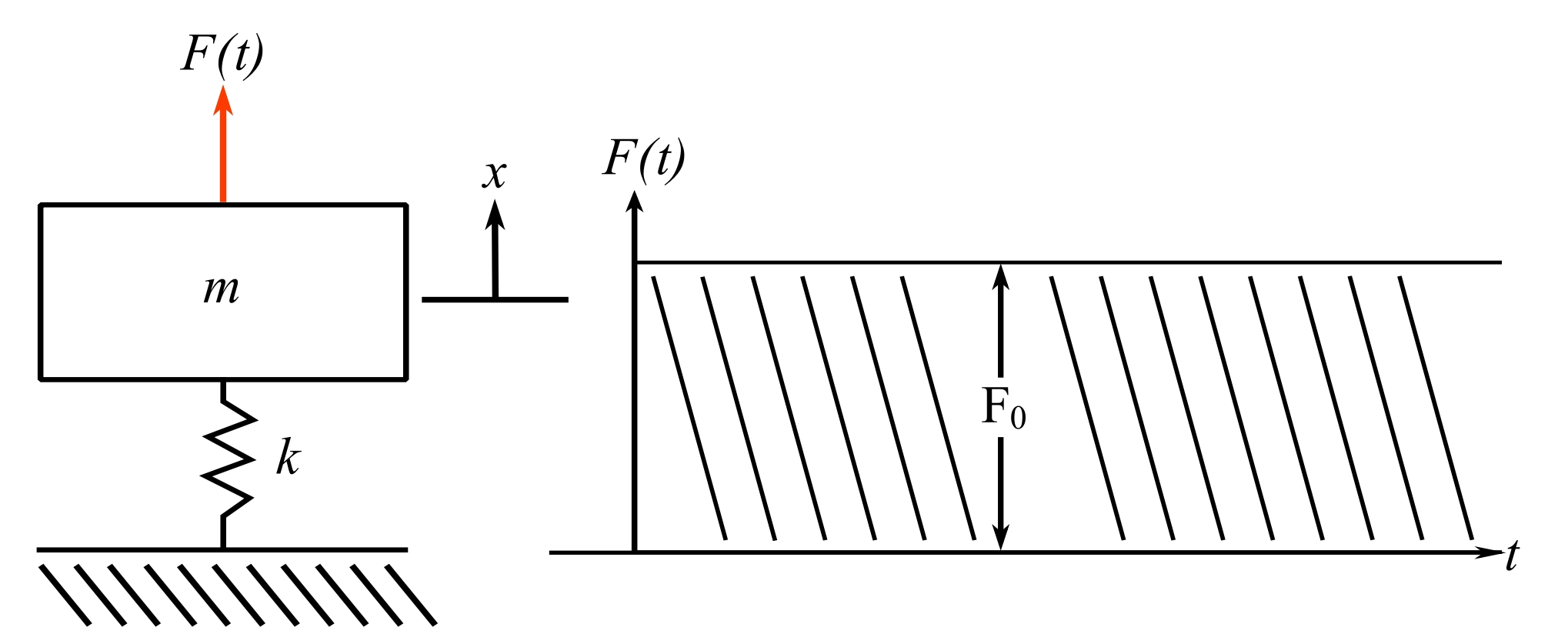
Consider first the undamped case for a step input:
Solution
![]()
![]()
Assume ![]()
![]()
![]()
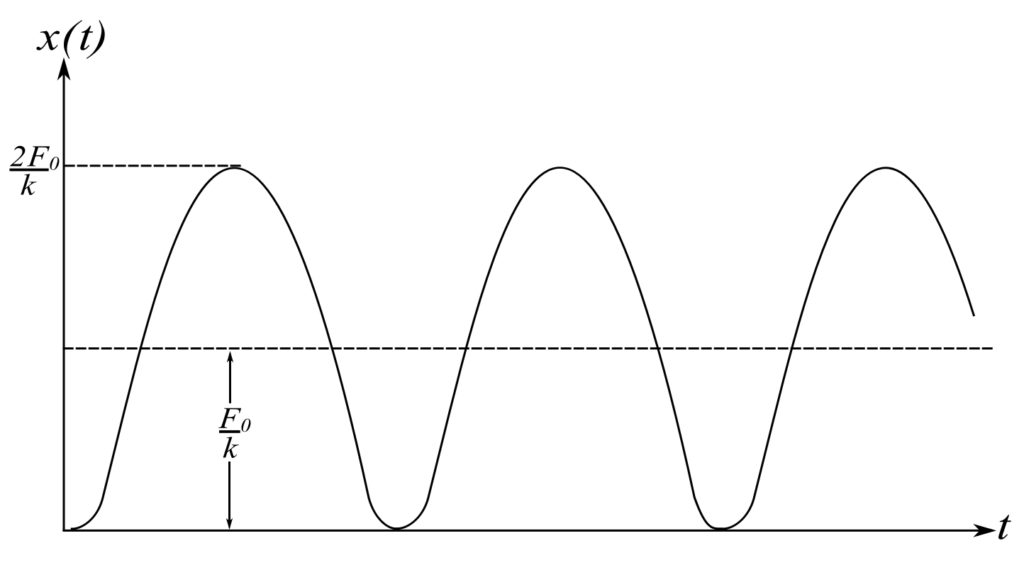
and the total solution:
![Rendered by QuickLaTeX.com \[\begin{split} x(t) &= x_H +x_p \\&= \frac{F_0}{k} + A\sin{pt} + B \cos{pt} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a5160ccacfe3857f0b89374f0035d17a_l3.png)
If ![]() , then:
, then:
![]()
![]()
![]()
While this case is straightforward, the solution is more difficult with damping or for different forcing functions.
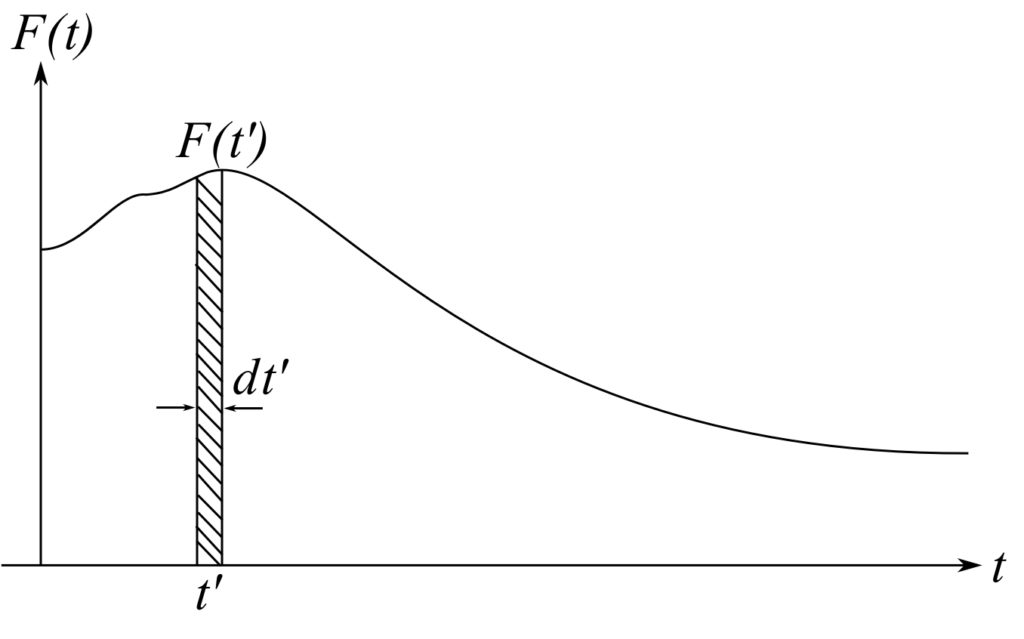
The response can be determined in a general form by considering ![]() as being made up from a series of short impulses. A general short impulse at some time
as being made up from a series of short impulses. A general short impulse at some time ![]() is shown. Consider what happens(response) if only this impulse is applied to the system:
is shown. Consider what happens(response) if only this impulse is applied to the system:
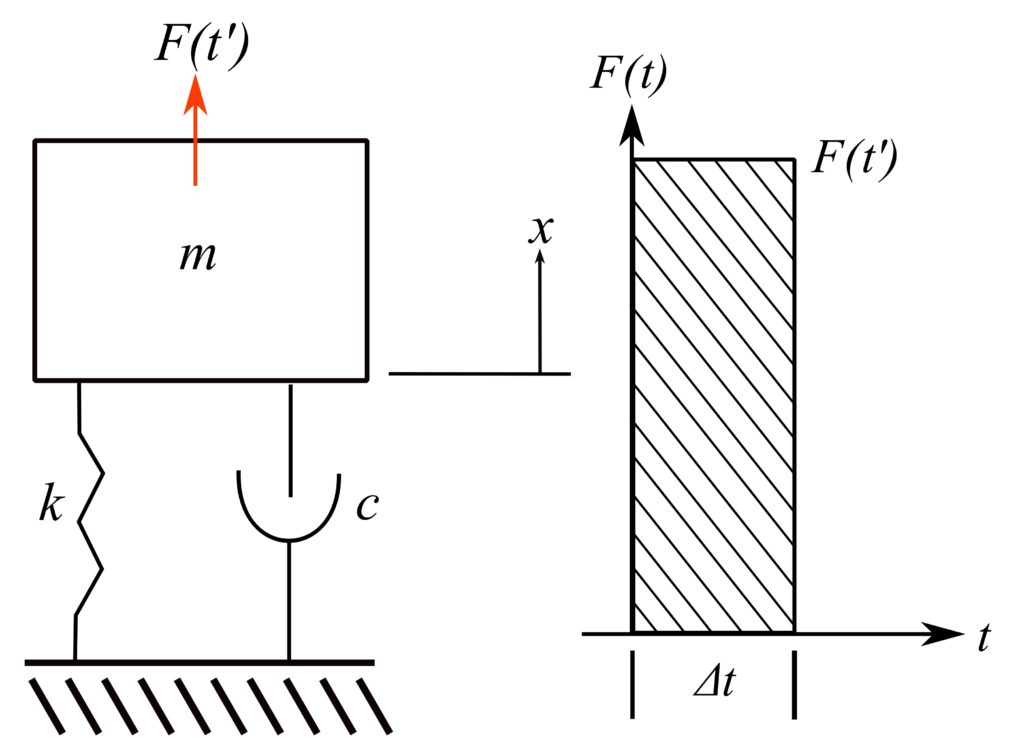
If ![]() is vanishingly small the impulse can be considered as changing the velocity of
is vanishingly small the impulse can be considered as changing the velocity of ![]() using impulses/momentum relations so that from initial
using impulses/momentum relations so that from initial ![]() (just before) to final
(just before) to final![]() condition:
condition:
![]()
Therefore:
![]()
This impulses will result in a free vibration with initial conditions:
![]()
![]()
If this is the only impulse then the response is:
![]()
with ![]()
![]()
![Rendered by QuickLaTeX.com \[ \begin{split}\dot{x}(0) &= B\sqrt{1-\zeta^2}p \\&= \frac{F(t')}{m}\Delta t \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2d639496b4402aab9624a378d7ae1dfb_l3.png)
![]()
Therefore:
![]()
Where ![]() is the time since the impulse.
is the time since the impulse.
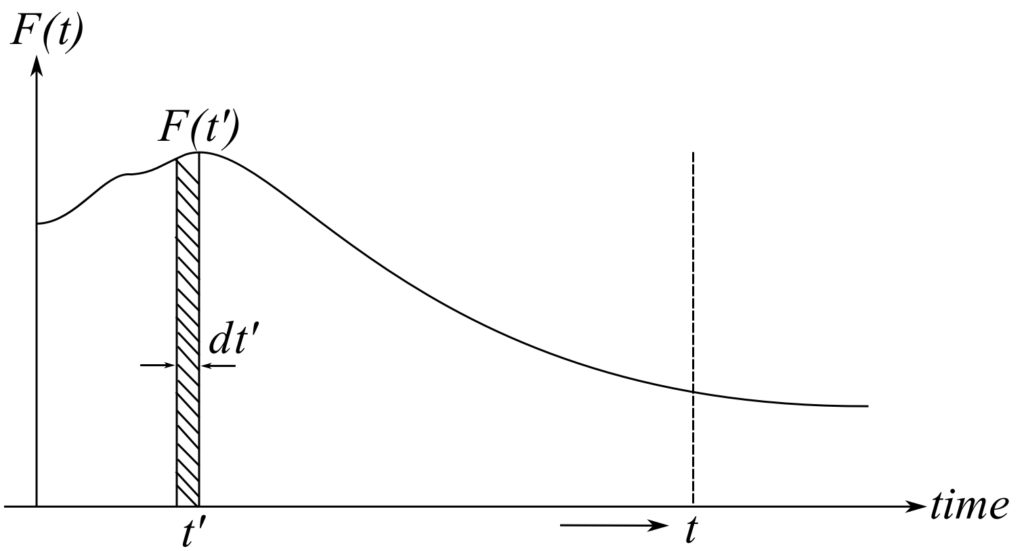
Therefore the response at ![]() due to the impulse at
due to the impulse at ![]() is
is ![]() :
:
![]()
The response due to all the impulses from ![]() to
to ![]() is the superposition of all the impulses’ response.
is the superposition of all the impulses’ response.
Therefore:
![]()
Assuming ![]() i.e. the mass was stationary prior to
i.e. the mass was stationary prior to ![]() being applied.
being applied.
For the step input ![]()
![]()
![]()
If the initial conditions are ![]() , then:
, then:
![Rendered by QuickLaTeX.com \[\begin{split}x(t) &= e\strut^{-\zeta pt}\biggr[x_0\cos{\sqrt{1-\zeta^2}}pt+\frac{v_0 + \zeta px_0}{\sqrt{1-\zeta^2}p}\sin{\sqrt{1-\zeta^2}pt}\biggr] \\&+\frac{1}{mp\sqrt{1-\zeta^2}} \int _0^\tau F(t')e^{\zeta p(t-t')}\sin{\sqrt{1-\zeta^2}p(t-t')}\,dt'\end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7f98fb0add8397760cdf92e15d4eec74_l3.png)
Example
For a package being dropped or for an airplane landing, a SDOF model can be utilized.
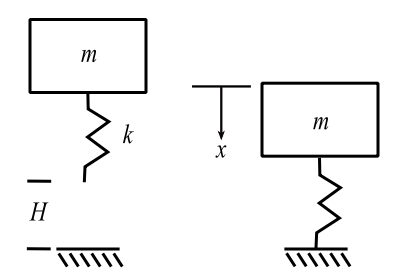
For the undamped case, as it strikes, ![]() and
and ![]() , and the forcing function is
, and the forcing function is ![]() (constant). NOTE:
(constant). NOTE: ![]() is not measured from the static equilibrium configuration. Using the general result:
is not measured from the static equilibrium configuration. Using the general result:
![Rendered by QuickLaTeX.com \[ \begin{split} x(t) &= \frac{\sqrt{2gH}}{p}\sin pt +\frac{1}{mp} \int_{0}^{t} mg\sin (t-t') dt' \\&= \frac{\sqrt{2gH}}{p}\sin pt + \frac{g}{p} \Big[\frac{\cos p(t-t')}{p}\Big]_{o}^{t} \\&= \frac{\sqrt{2gH}}{p}\sin pt + \frac{g}{p^2}\Big[1 - \cos pt \Big] \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ba2457ab77d3ffbd9a9a4091584a6065_l3.png)
![]()
![]()
Therefore, the maximum acceleration is:
![]()
![]()
With:
![Rendered by QuickLaTeX.com \[\begin{split} \delta_\text{ST} &= \frac{mg}{k} \\ &= \frac{p}{g^2} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2607cb4f31fe536cb3b364400708c7ec_l3.png)
In forensic studies of automobile collisions, the concern is the acceleration of a passenger’s head and the potential for internal damage. Assume the body/skull is modelled as a SDOF system.
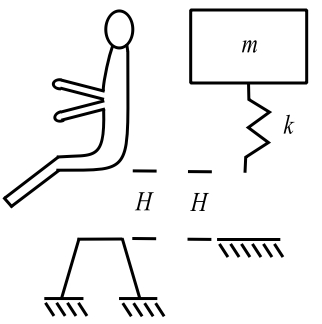
Biomechanical studies gives the spinal stiffness ![]() . Assume the person weighs 160 lbs and falls 6 inches because of being unrestrained. Thus:
. Assume the person weighs 160 lbs and falls 6 inches because of being unrestrained. Thus:
![Rendered by QuickLaTeX.com \[\begin{split} \delta_\text{ST} &= \frac{160}{458} \\&= 0.35 \ \text{inches} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b01e42aa49eddcdabc367b91c2b45ea5_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\ddot{x}_\text{MAX}}{g} &= -\sqrt{\frac{12}{0.35} + 1} \\&= -5.94 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4237cd444ccae1b652dbe22e98277fe2_l3.png)
If we add a seat cushion to the seat (cushion stiffness is ![]() ). What is the change in maximum acceleration?
). What is the change in maximum acceleration?
The effective stiffness is now:
![]()
![Rendered by QuickLaTeX.com \[\begin{split} k_\text{eff} &= \frac{(51)(458)}{458 + 51} \\& = \ 45.9 \text{ lbs/in} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-eba28e2de0545a9aea1c39a21c42da13_l3.png)
Thus:
![Rendered by QuickLaTeX.com \[\begin{split} \delta_\text{ST} &= \frac{160}{45.9} \\&= 3.49 \ \text{in} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d6bd723edea0439f5058931cf8e9b760_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\ddot{x}_\text{MAX}}{g} &= -\sqrt{\frac{12}{3.49} + 1} \\&= -2.1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1627ed10a2f2d9700b8846801ca5f637_l3.png)
The cushion reduces the acceleration drastically.
For many situations, the support of the system is subjected to the motion specified by its displacement, velocity, or acceleration.
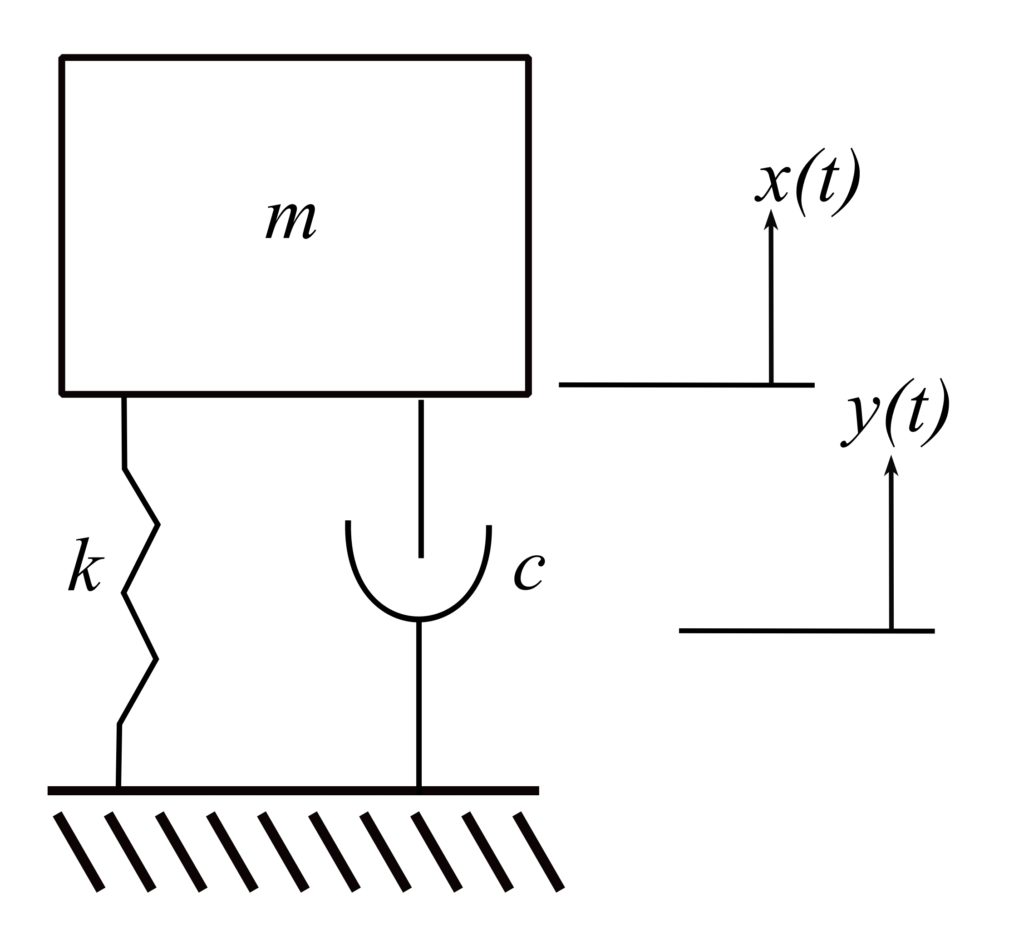
Therefore, for base acceleration:
![]()
![]()
Using the relative displacement ![]() :
:
![]()
The convolution integral for this case is:
![]()
The same approach can be used for a base excitation with velocity.
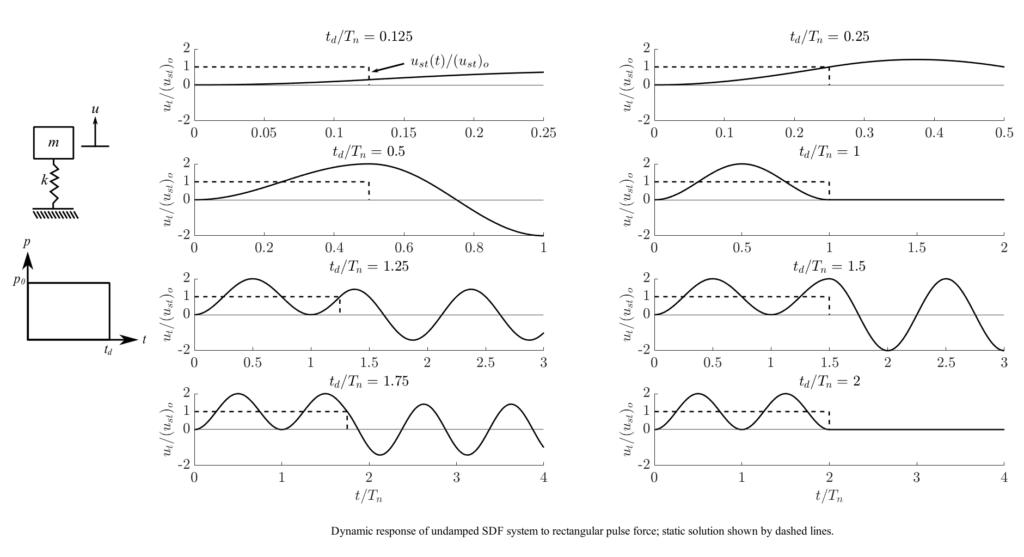
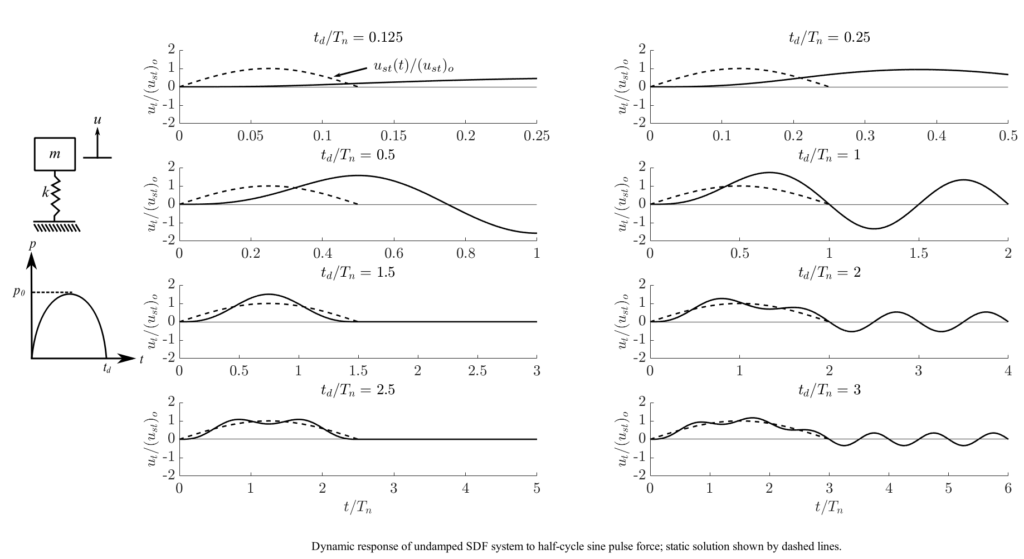
Examples of Dynamic Responses of Undamped SDF Systems to Different Pulse Forces
Note that the static solution is shown in the dashed lines.
Rectangular Pulse Force
Half Cycle Sine Pulse Force
Triangular Pulse Force
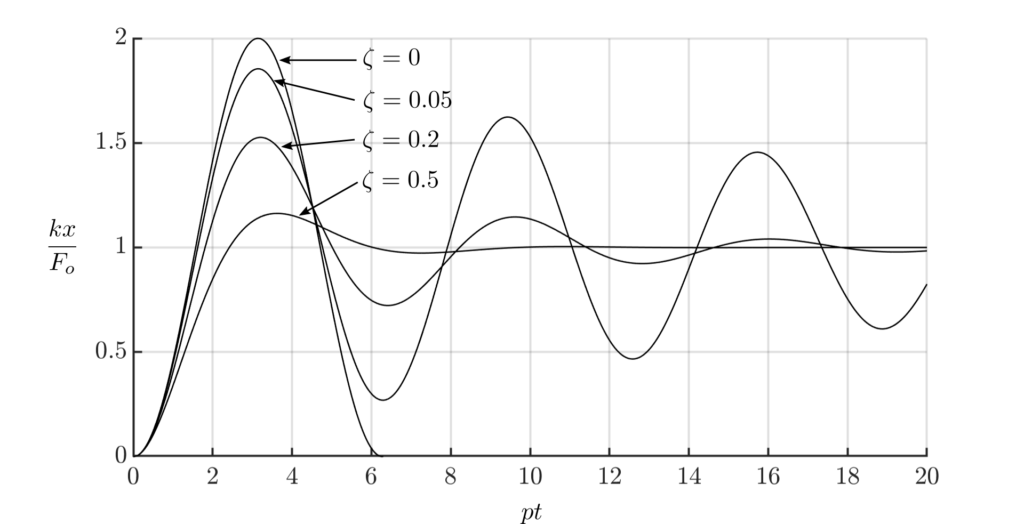
Shock Response Spectrum
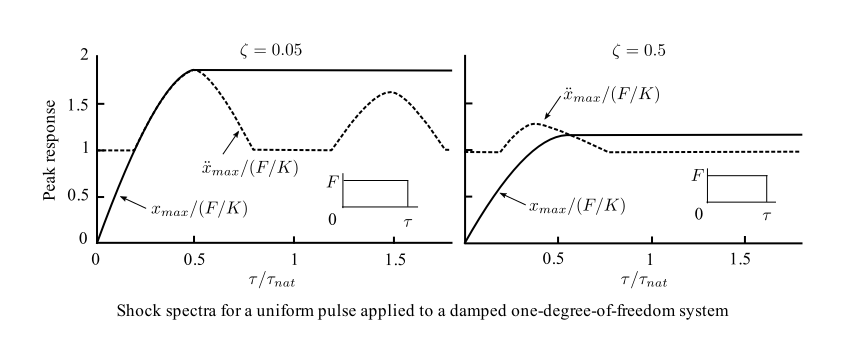
Previously we developed a technique to find the response of a damped spring mass system to an arbitrary excitation. When the duration of the pulse is small compared to the natural period (![]() ), the excitation is called a shock. It has been found that the concept of the shock response spectrum is useful for these situations.
), the excitation is called a shock. It has been found that the concept of the shock response spectrum is useful for these situations.
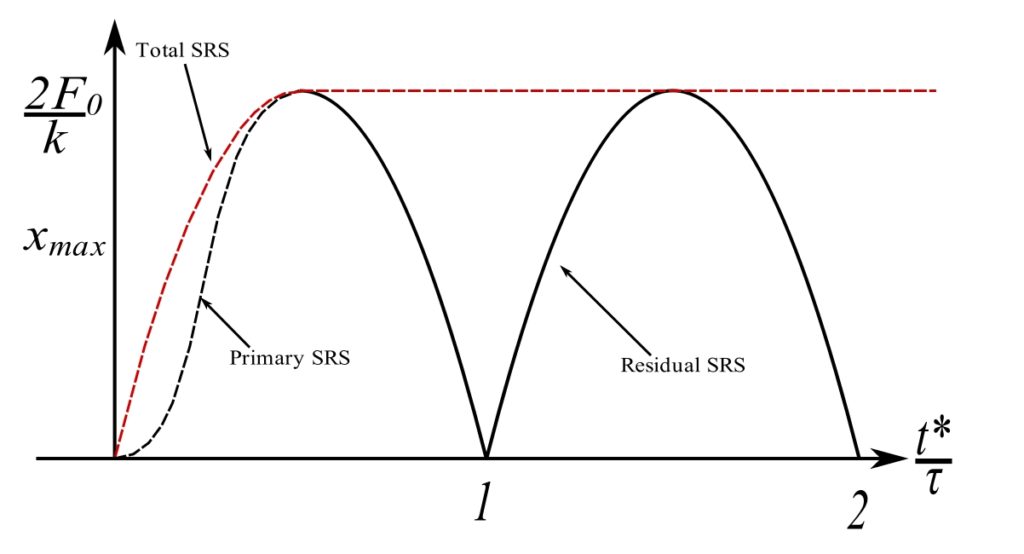
The Shock Response Spectrum (SRS) is a plot of the maximum peak response of a SDOF oscillator as a function of the natural period of the oscillator. The maximum of the peaks (called maxima) represents only a single point on the time response curve.
To illustrate the SRS concept consider a SDOF undamped system with no initial motion ![]() . The SRS is
. The SRS is
![]()
If F(t) is a rectangular pulse of length ![]()

then during the pulse
![]()
where ![]() and after
and after
![]()
where ![]() . Often the results are determined for the two sections (during & after) individually then combined as the primary response (during) and the residual (after pulse) response.
. Often the results are determined for the two sections (during & after) individually then combined as the primary response (during) and the residual (after pulse) response.
During the pulse
![]()
Where ![]() for a maximum:
for a maximum:
![]()
therefore:
![]()
![]()
therefore up to ![]() , the maximum is the value at the time considered as it is still increasing therefore:
, the maximum is the value at the time considered as it is still increasing therefore:
![]()
where ![]() . After
. After ![]() the maximum is:
the maximum is:
![Rendered by QuickLaTeX.com \[ \begin {split} x_\text{MAX} &=\frac{F_0}{k}\Big(1-\cos\Big(\frac{p\pi}{p}\Big)\Big) \\&=2\frac{F_0}{k} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-406bf8aa86a5dde9d7ed030a6b69f355_l3.png)
These results are called the primary values as they correspond to the result during the pulse.

after ![]()
![]()
where ![]()
and we find the maxima by differentiating
![]()
at ![]()
![]()
therefore:
![Rendered by QuickLaTeX.com \[ \begin{split} \sin pt_1(1-\cos pt^*) &= -\sin pt^* \cos pt_1 \\ \tan pt_1 &= \frac{-\sin pt^*}{(1-\cos pt^*)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8948307f1f54e748bb34e90014606e89_l3.png)
This value for ![]() must be inserted into the original expression to find the maximum displacement. This will require
must be inserted into the original expression to find the maximum displacement. This will require ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() .
.
therefore consider the triangle
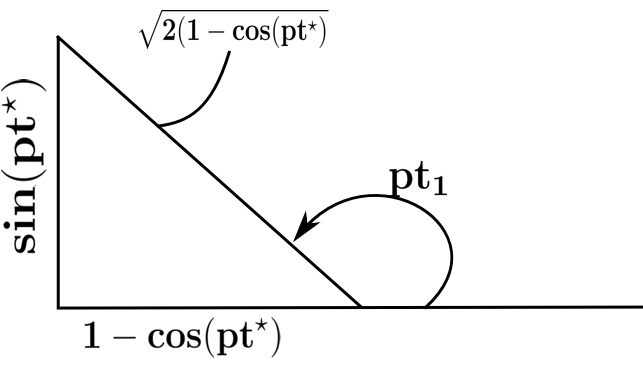
therefore:
![]()
![Rendered by QuickLaTeX.com \[\begin{split} \cos pt_1 &= \frac{-(1-\cos pt^*)}{\sqrt{2(1-\cos pt^*)}} \\ &= -\frac{1}{\sqrt{2}} \sqrt{1-\cos pt^*} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-27ace3993b2485f4aa9b4f245f103450_l3.png)
now
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{x(t_1)k}{F_0}\bigg|_{\text{MAX}} &= \cos pt^* \cos pt_1 + \sin pt^* \sin pt_1 - \cos pt_1 \\ &= -\frac{1}{\sqrt{2}}\sqrt{1-\cos pt^*}[-1+ \cos pt^*] + \frac{\sin^*2pt^*}{\sqrt{2(1-\cos pt^*}} \\ &=\frac{\frac{\sqrt{2}}{\sqrt{2}}(1-\cos pt^*)^2+\sin^*2pt^*}{\sqrt{2(1-\cos pt^*)}} \\ &= \frac{2(1-\cos pt^*)}{\sqrt{2(1-\cos pt^*)}} \\ &=\sqrt{2(1-\cos pt^*)} \\ &= 2\sin p\frac{t^*}{2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-07eae4b54125f825f76b142c6db2c16b_l3.png)
but ![]() therefore:
therefore:
![]()
Residual Response

The total SRS can now be determined
If damping is added then the magnitude can be reduced considerably. However, the calculation of the SRS must be done numerically
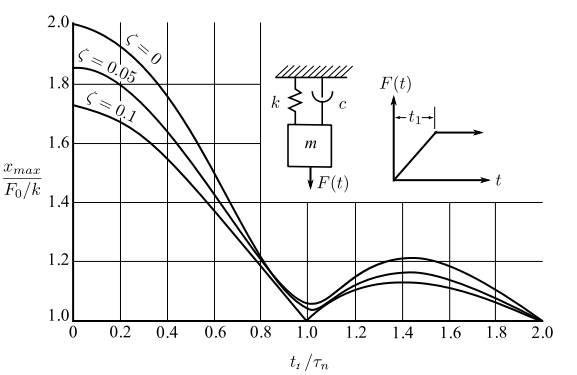
For cases which the pulses variation is less than one-half the period ![]() , the overall maximum occurs after the pulse in the “free” vibration phase. As the pulse duration compared to the period becomes smaller we can approximate the response where it is the magnitude of the impulse(not the details of the shape) that matters. In the development of the theory, the response for a damped system was:
, the overall maximum occurs after the pulse in the “free” vibration phase. As the pulse duration compared to the period becomes smaller we can approximate the response where it is the magnitude of the impulse(not the details of the shape) that matters. In the development of the theory, the response for a damped system was:
![]()
Where ![]() is the time since the impulse and for for the undamped situation
is the time since the impulse and for for the undamped situation
![]()
Where ![]() is the impulse,
is the impulse, ![]() , and the maximum displacement is:
, and the maximum displacement is:
![Rendered by QuickLaTeX.com \[\begin{split} x_\text{MAX} &= \frac{I}{mp} \\&= \frac{I}{k} \frac{k}{mp} \\&= \frac{Ip}{k} \\&= \frac{I}{k}\frac{2 \pi}{\tau} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0b4d4e25234c30e263e8523da26a2d61_l3.png)
Consider three different impulses:
1) rectangular 2) half sine 3) triangular
1)

![]()
Therefore, ![]() compared to the static response due to
compared to the static response due to ![]()
![]()
2)
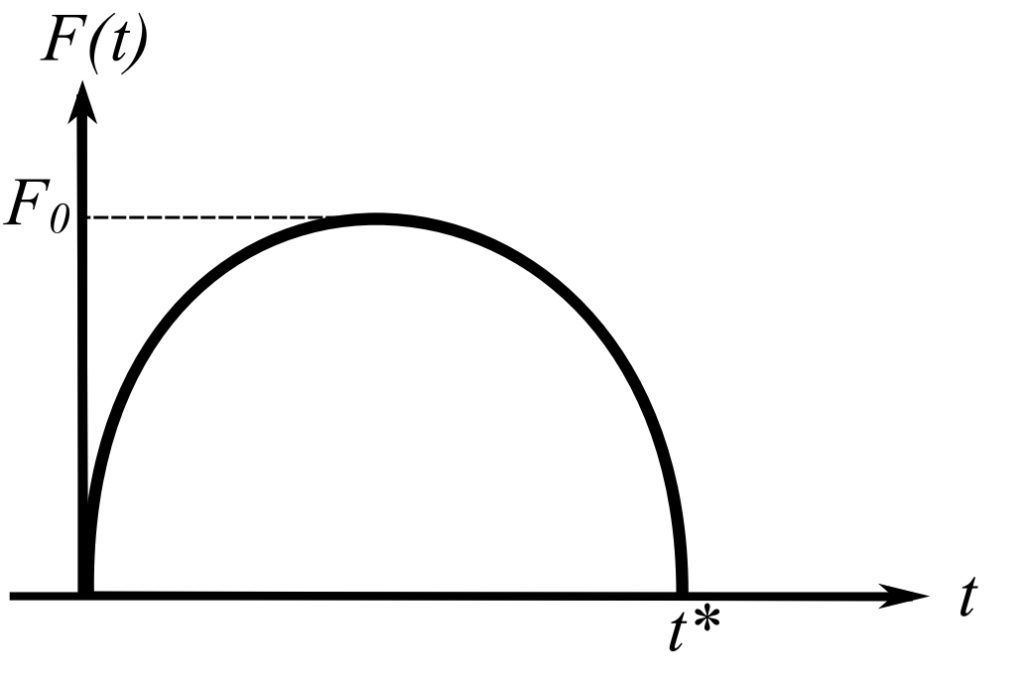
![Rendered by QuickLaTeX.com \[\begin{split} I &= F_o \int_{0}^{t^{\star}} \sin \frac{\pi t}{t^{\star}} \,dt \\&= -F_o \frac{t^{\star}}{\pi} \cos\frac{\pi t}{t^{\star}} \Big|_ 0^ {t^{\star}} \\&= \frac{2F_o t^{\star}}{\pi} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-583500cbc5ac28503497bba51f40e5e4_l3.png)
Therefore,
![Rendered by QuickLaTeX.com \[\begin{split} x_\text{MAX} &= \frac{2\pi}{\tau} \frac{2F_o t^{\star}}{\pi} \\&= \frac{4 t^{\star}}{\tau} (\frac{F_o}{k}) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-799f9150eb7871bc447475dac70606e4_l3.png)
3)
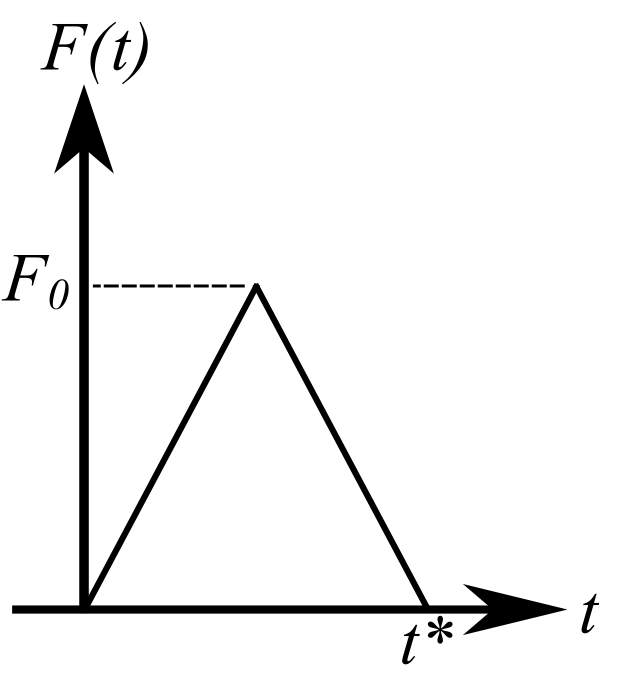
![]()
![]()
If the effect of damping is included then:
![]()
and for ![]() we assume the maximum occurs at (or near) where
we assume the maximum occurs at (or near) where ![]() is 1.
is 1.
Therefore ![]() (time at
(time at ![]() ) is
) is ![]() of a so-called damped period:
of a so-called damped period:
![Rendered by QuickLaTeX.com \[\begin{split} \hat{t} &= \frac{\pi}{2p \sqrt{1-\zeta ^{2}}} \\& \approx \frac{\pi}{2p} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9c384f90fadcacd1d3674e65cd07e355_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} x_\text{MAX} &= \frac{I}{mp} e\strut^{-\zeta p \hat{t}} \\&= \frac{I}{mp} e\strut^{-\zeta \frac{\pi}{2}} \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-234244550c0acc7ec664a130a6e8c1fd_l3.png)
and for ![]() :
:
![]()
and we can multiply the undamped values by ![]() :
:
| 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.3 | |
| 0.921 | 0.843 | 0.764 | 0.686 | 0.607 | 0.529 |
