Open Educational Resources

Review of single and multi-degree of freedom (mdof) systems: Steady State Harmonic Response

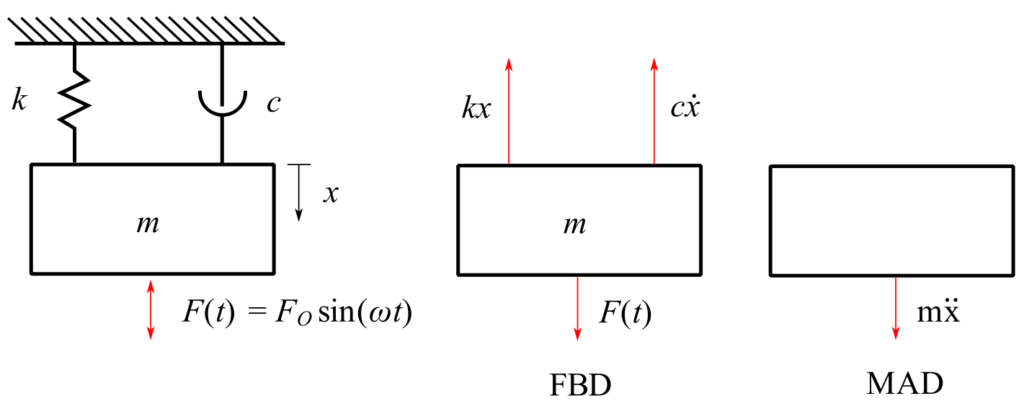
    \[ \begin{split}+\downarrow\sum F_x &= m\ddot{x} \\&= -kx-c\dot{x} + F(t) \end{split}\]

Therefore:

(\star)   \begin{equation*} m\ddot{x} + c\dot{x} + kx = F_0\sin(\omega t) \end{equation*}

Therefore find solution as homogeneous solution + particular integral.

a) Homogeneous Solution:

    \[ m\ddot{x_H} + c\dot{x_H} = 0 \implies\]

    \[ x_H = e^{-\zeta pt}\big[A\cos{\sqrt{1-\zeta^2}}pt+ B\sin{\sqrt{1-\zeta^2}}pt\big] \]

b) Particular integral:

Try x_p = C\sin{\omega t} + D\cos{\omega t} into (\star)

    \[-m\omega^2C\sin{\omega t} - m\omega^2D\cos{\omega t} + Cc\omega\cos{\omega t}\]

    \[-Dc\omega\sin{\omega t} + kC\sin{\omega t} + kD\cos{\omega t} = F_0\sin{\omega t} \]

Therefore:

    \[-m\omega^2C-c\omega D+kC = F_0,\]

    \[-m\omega^2D+c\omega C+kD = 0\]

    \[C\Big(1-\frac{m\omega^2}{k}\Big) - \frac{c\omega}{k}D = \frac{F_0}{k}\]

    \[C\Big(\frac{c\omega}{k}\Big) + \Big(1-\frac{m\omega^2}{k}\Big)D = 0\]

Note:

    \[ \frac{m\omega^2}{k} = \frac{\omega^2}{p^2}\]

    \[ \frac{c\omega}{k} = 2\zeta\frac{\omega}{p}\]

    \[ \begin{split} \implies \frac{c\omega}{k} &= \frac{c}{c_c}(2mp)\frac{\omega}{k} \\&= 2\zeta\frac{\omega}{p}\end{split}\]

Therefore:

    \[C\Big(1-\frac{\omega^2}{p^2}\Big) - 2\zeta\frac{\omega}{p}D = 0,\]

    \[2\zeta\frac{\omega}{p}C+\Big(1-\frac{\omega^2}{p^2}\Big)D = 0\]

Solving the above equations for C & D gives:

    \[C = \frac{\big(1-\frac{\omega^2}{p^2}\big)F_0/k}{\big(1-\frac{\omega^2}{p^2}\big)^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}\]

    \[D = \frac{-2\zeta\frac{\omega}{p}F_0/k}{\big(1-\frac{\omega^2}{p^2}\big)^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}\]

when x(0) = x_0 and \dot{x} = v_0:

    \[x(t) = e^{-\zeta pt}\Big[x_o\cos{\sqrt{1-\zeta^2}}pt + \frac{v_0+\zeta px_0}{\sqrt{1-\zeta^2}}\sin{\sqrt{1-\zeta^2}}pt\Big]+C\sin{\omega t} +D\cos{\omega t}\]

However, if \zeta is +ve after some time the homogeneous part will decay and the steady state solution becomes:

    \[X(_{ss}) = C\sin{\omega t} + D\cos{\omega t}\]

If we take the special case of no clamping, the homogeneous equation is:

    \[m\ddot{x}_H + kx_H = 0\]

    \[ x_H = A\cos{pt} + B\sin{pt}\]

and the particular integral is

    \[x_p = C\sin{\omega t} \]

Therefore:

    \[m\ddot{x}_p+kx_p = F_0\sin{\omega t}\]

    \[(-mC\omega^2+ck)\sin{\omega t} = F_0\sin{\omega t}\]

Therefore:

    \[ \begin{split} C &= \frac{F_0}{k-m\omega^2} \\&= \frac{\frac{F_0}{k}}{1-\frac{\omega^2}{p^2}} \end{split} \]

Therefore the total solution is:

    \[ x = A\cos{pt} +B\sin{pt} + \frac{F_o/k}{1-\frac{\omega^2}{p^2}}\sin{\omega t} \]

Note that as there is no damping present that the homogeneous solution does not \rightarrow 0 as time increases.

    \[x_{ss} = C\sin{\omega t} + D\cos{\omega t}\]

and we combine them to get:

    \[ \begin{split} x_{ss} &= \sqrt{C^2+D^2}\sin{(\omega t - \phi)} \\&= \frac{\frac{F_0}{k}}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}\sin{(\omega t - \phi)} \end{split} \]

Where:

    \[ \tan{\phi} = \frac{2\zeta\frac{\omega}{p}}{1-\frac{\omega^2}{p^2}} \]

This result is extremely useful in practical situations especially for controlling noise and vibration.

While this tells us the dynamic motion of the system, there is still the static deflection of the springs to be remembered. These are also related situations which are obtained by reconsideration of the fundamental equation of motion.

From the view of real situations, these are other quantities that are of interest. One of these is the force F_T transmitted to the supporting structure.

    \[F_T = kx +c\dot{x}\]

Where x is:

    \[x = \frac{F_0/k}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}\sin{(\omega t - \phi)}\]

Therefore:

    \[F_T = \frac{F_0/k}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}} \Big[k\sin{(\omega t - \phi)} + c\omega\cos{(\omega t - \phi)}\Big]\]

and the magnitude of F_T,\big|F_T\big| (using the fact that \frac{c\omega}{k} = 2\zeta\frac{\omega}{p}) is:

    \[\big|F_T\big| = \frac{\sqrt{k^2+(c\omega)^2}}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}\]

    \[\frac{|F_T|}{F_0} = \frac{\sqrt{1+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}\]

A second practical situation occurs when the structure is vibrating and we wish to isolate a machine from the vibration (base excitation).

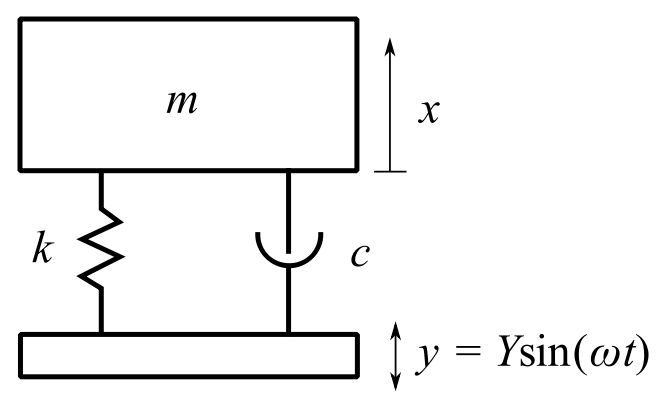
So the equation of motion is:

    \[m\ddot{x} + c\dot{x} + kx = kY\sin{\omega t}+ c\omega Y\cos{\omega t} \]

The steady state solution comes from the assumption from x(t):

    \[ \begin{split} x(t) &= C_1 \sin{\omega t} + C_2 \cos{\omega t} \\& \equiv X\sin{(\omega t - \phi)} \end{split}\]

and the solution is:

    \[X = \frac{Y\sqrt{1+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2+\big(2\zeta\frac{\omega}{p}\big)\strut^2}}\]

    \[ \phi = \arctan{\biggr(\frac{2\zeta\frac{\omega}{p}}{1-\frac{\omega^2}{p^2}}\biggr)}\]

A third potential situation is essentially the original forced situation where the magnitude of the forcing function is due to rotating imbalance:

    \[F_0 = me\omega^2\]

Where past of the mass M, \tilde{m}, at an eccentricity e causes the dynamic force.

Equations of motion:

    \[ (M-\tilde{m})\ddot{x} + \tilde{m}\frac{d^2}{dt^2}(x+e\sin{\omega t}) = -kx - c\dot{x} \]

    \[ M\ddot{x} + c\dot{x} + kx = \tilde{m}e\omega^2\sin{\omega t} \]

This looks like the previous forced case where F_o is replaced with \tilde{m}e\omega^2 so that:

    \[X = \frac{\tilde{m}e\omega^2}{\sqrt{(k-M\omega^2)^2+(c\omega)^2}}\]

and reduced to non-dimensional form as:

    \[\frac{MX}{\tilde{m}e} = \frac{ \omega^2/p^2}{\sqrt{\big(1-\frac{\omega}{p}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\]

so that the steady state solution is:

    \[x(t) = X\sin{(\omega t - \phi)}\]

where:

    \[ \tan{\phi} = \frac{2\zeta\frac{\omega}{p}}{1-\big(\frac{\omega}{p}\big)\strut^2}\]

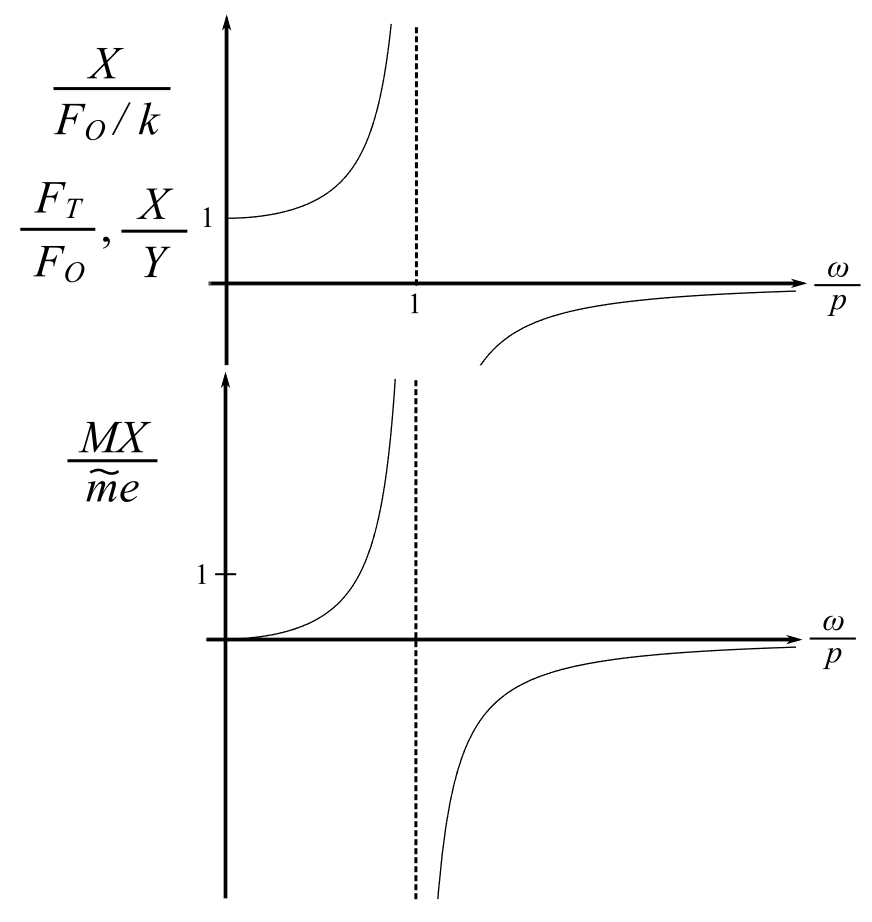
The frequency response for all these cases are summarized below.

Single Degree of Freedom Systems – Useful Relations

The frequency response curves are helpful in visualizing where the specific system you are analyzing lies. It must be remembered that there is a phase difference between excitation and response with the change from being nearly in phase to being nearly 180 degrees out of phase. The transition occurs near resonance (\frac{\omega}{p} = 1). For the undamped case, this means the response is undefined at \frac{\omega}{p} and the response becomes:

    \[ \begin{split} \left|\frac{X}{Y}\right| &= \left|\frac{F_T}{F_0}\right| \\&= \left|\frac{X}{X_0}\right| \\& = \frac{1}{1-\frac{\omega^2}{p^2}}, \frac{\omega}{p} < 1\\& = \frac{1}{\frac{\omega^2}{p^2}-1}, \frac{\omega}{p} > 1 \end{split} \]

    \[\left| \frac{MX}{\tilde{m}e}\right| = \frac{\omega^2/p^2}{1-\frac{\omega^2}{p^2}}, \frac{\omega}{p} < 1\]

    \[\left| \frac{MX}{\tilde{m}e}\right| = \frac{\omega^2/p^2}{\frac{\omega^2}{p^2}-1}, \frac{\omega}{p} > 1\]

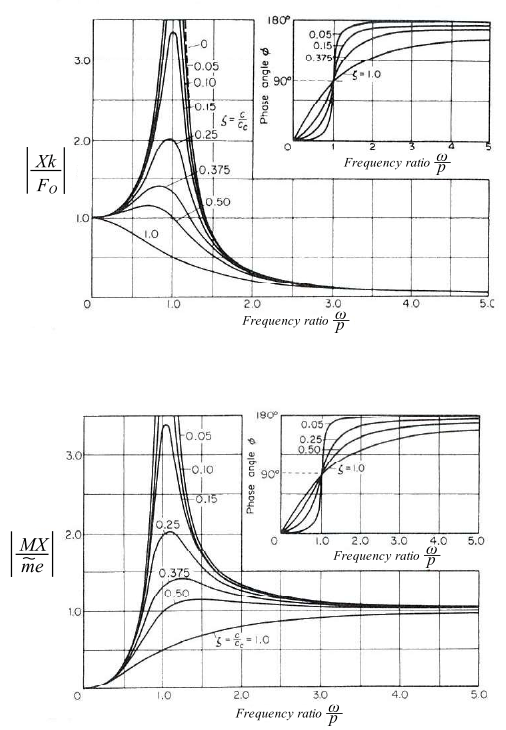
The results for the steady state forced single degree of freedom systems are usually present in the form of graphs showing various non-dimensional parameters. Because of the technical importance of these results, it is necessary to understand the differences between these representations. Two of the most useful are given by the expressions for displacement of the mass:

    \[\left|\frac{X}{X_0}\right| = \left|\frac{1}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\right|(A)\]

And the displacement of the main mass in the case of rotating imbalance:

    \[\left| \frac{MX}{\tilde{m}e}\right| = \left|\frac{\omega^2/p^2}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\right|(B)\]

a) Show that (B) can be derived from (A) for the special case in which the forcing function is due to rotating imbalance

b) For the undamped case determine the result of (A) and (B) both below and above resonance

a) Special cases for rotating imbalance:

    \[\left|\frac{X}{X_0}\right| = \left|\frac{1}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\right|(A)\]

    \[\left| \frac{MX}{\tilde{m}e}\right| = \left|\frac{\omega^2/p^2}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\right|(B)\]

    \[X_0 = \frac{F_0}{k}\]

If F_0 = \tilde{m}e\omega^2:

    \[ X_0 = \frac{\tilde{m}e\omega^2}{k}\]

    \[\frac{xk}{\tilde{m}e\omega^2} = \frac{1}{\sqrt{\big(1-\frac{\omega^2}{p^2}\big)\strut^2 + \big(2\zeta\frac{\omega}{p}\big)\strut^2}}\]

    \[\frac{Mxk}{M\tilde{m}e\omega^2} = \frac{xp^2M}{\tilde{m}e\omega^2}\]

Note: M includes the imbalanced mass \tilde{m}

b) \left|\frac{X}{X_0}\right| for \zeta \rightarrow 0 is:

    \[\begin{split} \left|\frac{X}{X_0}\right| &= \left|\frac{1}{\sqrt{1-\frac{\omega^2}{p^2}}}\right|, \frac{\omega}{p}\neq 1 \\&= \frac{1}{1-\frac{\omega^2}{p^2}}, \frac{\omega}{p}< 1 \\&= \frac{1}{\frac{\omega^2}{p^2}-1}, \frac{\omega}{p}> 1\end{split}\]

    \[\begin{split} \left| \frac{MX}{\tilde{m}e}\right|&= \left|\frac{\omega^2/p^2}{\sqrt{1-\frac{\omega^2}{p^2}}}\right|, \frac{\omega}{p}\neq 1 \\&= \frac{\omega^2/p^2}{1-\frac{\omega^2}{p^2}}, \frac{\omega}{p} < 1 \\&= \frac{\omega^2/p^2}{\frac{\omega^2}{p^2}-1}, \frac{\omega}{p} > 1 \end{split}\]

There are two important physical phenomena that are easily illustrated using the forced undamped SDOF system as we approach resonance. The entire solution:

    \[x(t) = C_1\cos pt + C_2 \sin pt + \frac{F_o}{k}\frac{\sin \omega t}{1-\frac{\omega^2}{p^2}}\]

Consider the case x(0)=0, \dot{x}(0)=0 (starting with no motion).

From the first of these C_1 = 0 and

    \[ \dot{x}(t) = C_2p\cos pt+\frac{F_o}{k}\frac{1}{1-\frac{\omega^2}{p^2}} \omega \cos \omega t \]

Therefore at t = 0:

    \[ \begin{split} C_2 &= \frac{-F_o}{k}\frac{\frac{\omega}{p}}{1-\frac{\omega^2}{p^2}} \\&=\frac{-F_o}{k}\frac{\omega p}{p^2-\omega^2} \end{split} \]

    \[ x(t) = \frac{F_o}{k}\frac{p^2}{p^2-\omega^2}\big[\sin \omega t-\frac{\omega}{p}\cos pt\big] \]

If p-\omega = 2\Delta, where \Delta is small compared to \omega or p, then:

    \[ x(t) = \frac{F_op^2}{k}\frac{1}{p^2-\omega^2}\big[\sin \omega t - \sin pt\big] \]

(\sin A- \sin B = 2\sin\frac{A-B}{2}\cos\frac{A+B}{2}), therefore:

    \[ x = 2\frac{F_op^2}{k(p^2-\omega^2)}\cos \omega t\sin\Delta t \]

    \[ \begin{split} p^2-\omega^2 & = (2\Delta + \omega)^2 - \omega^2 \nonumber \\ & = 4\Delta+4\Delta \omega \nonumber \end{split} \]

Therefore:

    \[ x = \frac{-F_o}{2k\Delta}\cos\omega t \sin\Delta t \]

This expression can be considered as representing a vibration with period 2\pi /\omega that has a slowly varying amplitude equal to \frac{F_o\omega}{2k\Delta}\sin\Delta t, (\sin\Delta t has a much longer period than \cos\omega t)

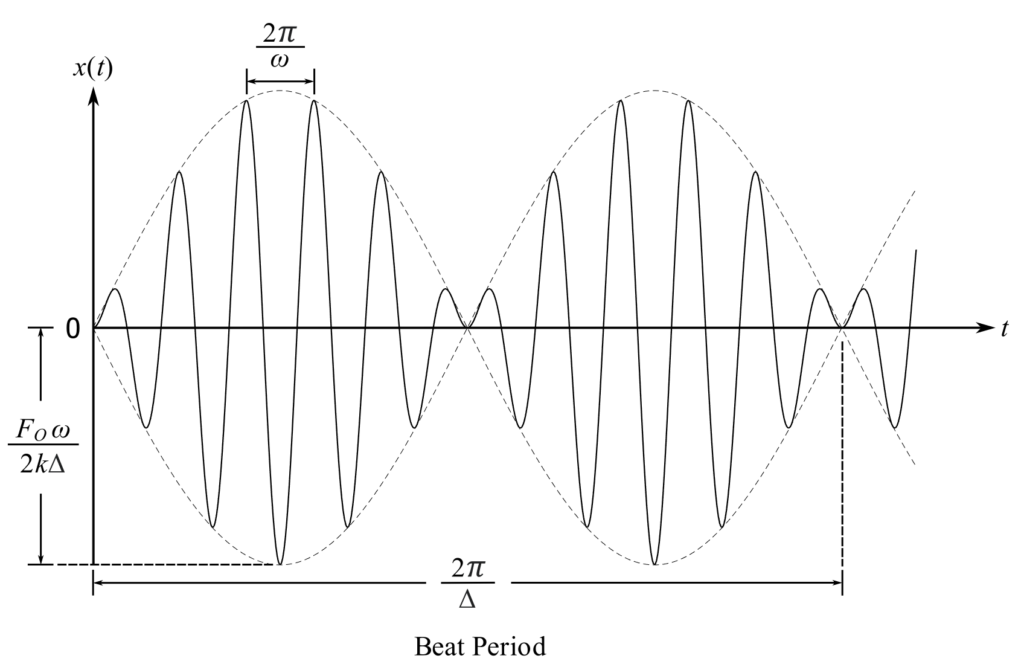
While the original solution to the forced undamped differential equation is not valid at \omega=p, it is of value to consider what happens at \Delta \rightarrow 0 for the displacement. Using  L’Hospital’s rule for the following limit:

    \[ \begin{split} \lim_{\Delta \to 0} \biggr(\frac{-F_o\omega}{2k}\cos\omega t \frac{\sin \Delta t}{\Delta} \biggr) &= \frac{-F_o \omega}{2k} \cos(\omega t) t\cos \Delta t \\&= \frac{-F_o\omega}{2k}t\cos\omega t \end{split} \]

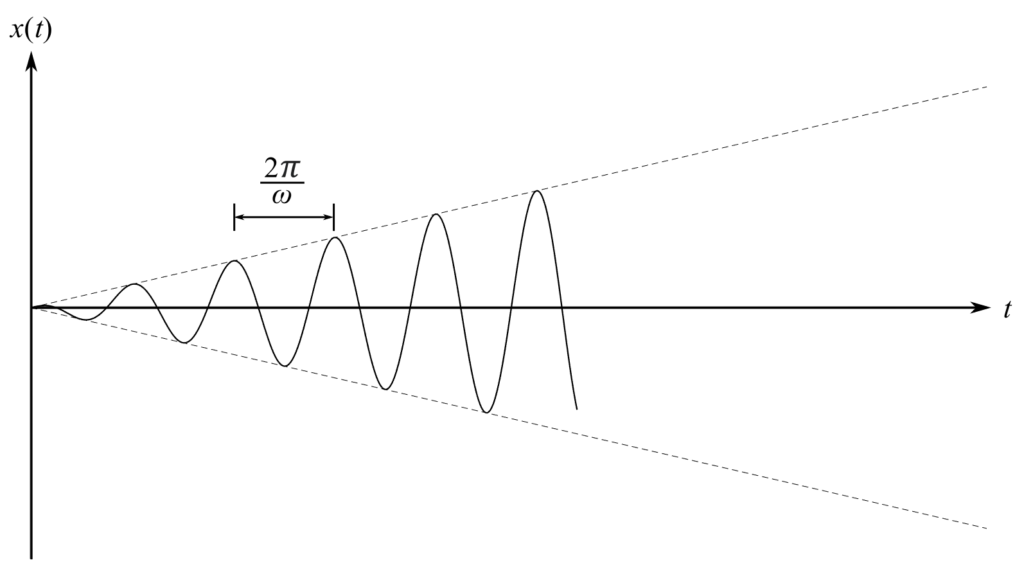
The amplitude of vibration increases indefinitely with time and the infinite amplitude is in the steady state. This means that to operate the system it is important to move through resonance as quickly as possible so that the amplitude does not “build up”.

Leave a Reply

Your email address will not be published.