Introduction to Numerical Analysis: Ordinary Differential Equations
Ordinary Differential Equations (ODEs) are equations that relate the derivatives of one or more smooth functions with an independent variable ![]() . The term “ordinary” indicates that there is only one independent variable appearing in the equations.
. The term “ordinary” indicates that there is only one independent variable appearing in the equations.
Examples of Ordinary Differential Equations
ODEs appear naturally in almost all engineering applications. Here are some examples:
Newton’s Second Law of Motion
One of the most ubiquitously used ordinary differential equations is Newton’s second law of motion, which relates the second derivative of the position of a particle (i.e., the acceleration) to the applied force on the particle. The relationship has the form:
![]()
where ![]() is the mass of the particle. The time
is the mass of the particle. The time ![]() is the independent variable, while the dependent variable is the position
is the independent variable, while the dependent variable is the position ![]() . Newton’s equation adopts different forms depending on the application. For example, if the applied force is the combined action of gravity and a spring with a constant
. Newton’s equation adopts different forms depending on the application. For example, if the applied force is the combined action of gravity and a spring with a constant ![]() (Figure 1), then the equation has the form:
(Figure 1), then the equation has the form:
![]()
The explicit solution to this equation has the following form:
![]()
where ![]() and
and ![]() are constants that depend on the initial conditions of the problem. If the initial displacement and velocity are equal to zero, i.e.,
are constants that depend on the initial conditions of the problem. If the initial displacement and velocity are equal to zero, i.e., ![]() and
and ![]() , then, the explicit solution has the form:
, then, the explicit solution has the form:
![]()
The following code utilizes the built-in DSolve function in Mathematica to solve the above simple equations. Also, the Manipulate built-in function is used to visualize the effect of varying ![]() and
and ![]() on the resulting vibration of the system.
on the resulting vibration of the system.
Clear[x, g, k, m]
(*General Solution*)
a = DSolve[m*x''[t] == m*g - k*x[t], x, t];
Print["General Solution="]
x = x[t] /. a[[1]]
(*Solution with initial velocity and displacement =0*)
Clear[m, g, x, k]
a = DSolve[{m*g - k*x[t] == m*x''[t], x[0] == 0, x'[0] == 0}, x, t];
Print["Solution with initial velocity and displacement =0"]
x = x[t] /. a[[1]]
Manipulate[g = 1;
Graphics3D[{Cuboid[{-1, -1, -5}, {0, 0, (g*m - g*m*Cos[Sqrt[k/m]*t])/k}]}, Axes -> True, PlotRange -> {{-1, 0}, {-1, 0}, {-5, 2*5/1}}, AxesOrigin -> {0, 0, 0}, ViewVertical -> {0, 0, -1}], {t, 0, 4*Pi*Sqrt[5]}, {m, 1, 5}, {k, 1, 5}]
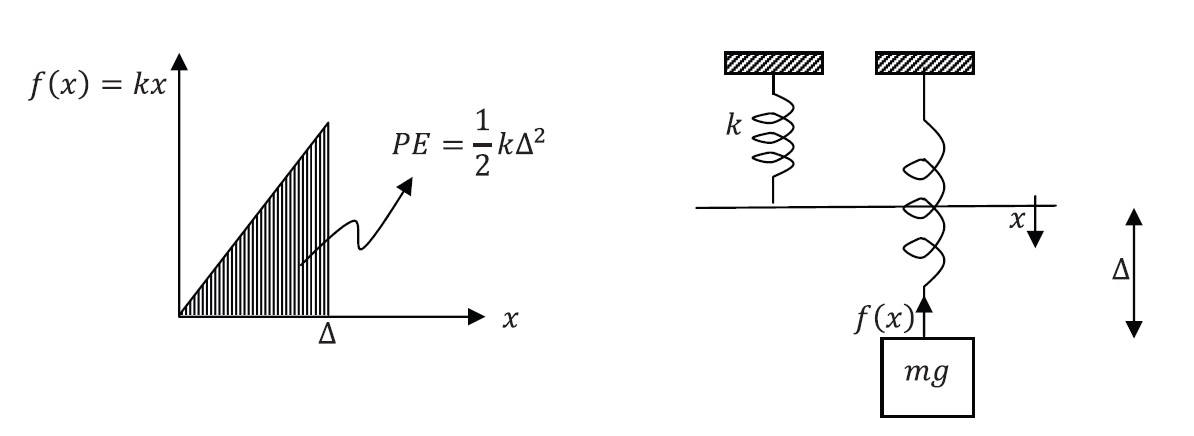
Figure 1. Mass – Linear Elastic Spring System
If the external forces include a damping force (a force that is a function of the velocity and that is always opposite to the direction of motion), then, the equation has the form:
![]()
where ![]() is the damping coefficient.
is the damping coefficient.
The explicit solution to this equation has the following form:
![]()
where ![]() and
and ![]() are constants that depend on the initial conditions of the problem. If the initial displacement and velocity are equal to zero, i.e.,
are constants that depend on the initial conditions of the problem. If the initial displacement and velocity are equal to zero, i.e., ![]() and
and ![]() , then, the explicit solution has the form:
, then, the explicit solution has the form:
![Rendered by QuickLaTeX.com \[ x=-\frac{m e^{-\frac{t \left(\sqrt{\beta^2-4 k m}+\beta\right)}{2 m}} \left(\beta \left(e^{\frac{t \sqrt{\beta^2-4 k m}}{m}}-1\right)+\sqrt{\beta^2-4 k m} \left(e^{\frac{t \sqrt{\beta^2-4 k m}}{m}}-2 e^{\frac{t \left(\sqrt{\beta^2-4 k m}+\beta\right)}{2 m}}+1\right)\right)}{2 k \sqrt{\beta^2-4 k m}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-78adadb04b6b3dc3354d80462784de4e_l3.png)
The following code utilizes the built-in DSolve function in Mathematica to solve the above simple equations. Also, the Manipulate built-in function is used to visualize the effect of varying ![]() ,
, ![]() , and
, and ![]() on the resulting vibration of the system.
on the resulting vibration of the system.
Clear[x, g, k, m]
(*General Solution*)
a = DSolve[m*x''[t] == m*g - k*x[t] - beta*x'[t], x, t];
Print["General Solution (damped system)="]
x = x[t] /. a[[1]]
(*Solution*)
Clear[x, g, k, m, beta]
a = DSolve[{m*x''[t] == m*g - k*x[t] - beta*x'[t], x[0] == 0, x'[0] == 0}, x, t];
Print["Solution with initial velocity and displacement =0"]
x = x[t] /. a[[1]];
x = Simplify[x]
Manipulate[g = 1;Graphics3D[{Cuboid[{-1, -1, -5}, {0, 0, -((E^(-(((beta + Sqrt[beta^2 - 4 k m]) t)/(2 m)))m (beta (-1 + E^((Sqrt[beta^2 - 4 k m] t)/m)) + (1 + E^((Sqrt[beta^2 - 4 k m] t)/m)-2 E^(((beta + Sqrt[beta^2 - 4 k m]) t)/(2 m))) Sqrt[beta^2 - 4 k m]))/(2 k Sqrt[beta^2 - 4 k m]))}]}, Axes -> True, PlotRange -> {{-1, 0}, {-1, 0}, {-5, 10}}, AxesOrigin -> {0, 0, 0}, ViewVertical -> {0, 0, -1}], {t, 0, 2*4*Pi*Sqrt[5]}, {m, 1, 5}, {beta, 0, 5}, {k, 1, 5}]
Beam Deflection
The deflection of an Euler-Bernoulli beam follows the following equation:
![]()
where ![]() is the beam’s Young’s modulus,
is the beam’s Young’s modulus, ![]() is the cross sectional moment of inertia,
is the cross sectional moment of inertia, ![]() is the beam’s deflection (the dependent variable),
is the beam’s deflection (the dependent variable), ![]() is the applied distributed load on the beam, and
is the applied distributed load on the beam, and ![]() is the position along the beam’s length (the independent variable). For a fixed-ends beam; if the deflection and rotation at both ends of a beam of length
is the position along the beam’s length (the independent variable). For a fixed-ends beam; if the deflection and rotation at both ends of a beam of length ![]() is equal to zero, i.e.
is equal to zero, i.e. ![]() , and if
, and if ![]() is constant, then, the deflection of the beam has the form:
is constant, then, the deflection of the beam has the form:
![]()
Growth and Decay
If ![]() is the number of organisms at any time
is the number of organisms at any time ![]() , and if the growth of the number depends on the number that is already there, then, the ODE that would describe this uninhibited growth is given by:
, and if the growth of the number depends on the number that is already there, then, the ODE that would describe this uninhibited growth is given by:
![]()
Where ![]() is a positive constant. The time
is a positive constant. The time ![]() is the independent variable, while the dependent variable is the number of organisms
is the independent variable, while the dependent variable is the number of organisms ![]() . The general solution of this equation has the form:
. The general solution of this equation has the form:
![]()
where ![]() is a constant depending on the boundary conditions. If the initial condition is such that
is a constant depending on the boundary conditions. If the initial condition is such that ![]() then, the solution has the form:
then, the solution has the form:
![]()
Similarly, if rate of decrease (decay) of a quantity is a function of the amount available, then, the uninhibited decay can be described by the equation:
![]()
where ![]() is a positive constant. The time
is a positive constant. The time ![]() is the independent variable, while the dependent variable is the quantity
is the independent variable, while the dependent variable is the quantity ![]() . Radioactive decay follows this ODE. The general solution of this equation has the form:
. Radioactive decay follows this ODE. The general solution of this equation has the form:
![]()
where ![]() is a constant depending on the boundary conditions. If the initial condition is such that
is a constant depending on the boundary conditions. If the initial condition is such that ![]() then, the solution has the form:
then, the solution has the form:
![]()
The following tool plots the quantities ![]() or
or ![]() when
when ![]() for different values of the exponent:
for different values of the exponent:
Clear[x]
a = DSolve[x'[t] == k*x[t], x, t];
x = x[t] /. a[[1]]
Clear[x]
a = DSolve[{x'[t] == k*x[t], x[0] == A}, x, t]
x = x[t] /. a[[1]]
Manipulate[A = 1; r = Grid[{{"k=", k}}, Spacings -> 0]; Grid[{{Plot[A*E^(k*t), {t, 0, 20}, AxesLabel -> {"t", "x(t) or y(t)"}, ImageSize -> Medium]}, {r}}], {k, -0.5, 0.5}]
Electrical Capacitors and Inductors
Simple electric circuits are composed of three components: resistances, capacitors, and inductors. The relationship between the voltage drop ![]() across a resistance, and the current
across a resistance, and the current ![]() passing through it is given by:
passing through it is given by:
![]()
where ![]() is the constant of proportionality, namely the value of the electric resistance. A capacitor on the other hand is an element that has the following relationship between the current passing through it
is the constant of proportionality, namely the value of the electric resistance. A capacitor on the other hand is an element that has the following relationship between the current passing through it ![]() and the rate of change of the voltage drop across it
and the rate of change of the voltage drop across it ![]() :
:
![]()
where ![]() is the constant of proportionality, namely the capacitance. An inductor is an element that has the following relationship between the voltage drop across it
is the constant of proportionality, namely the capacitance. An inductor is an element that has the following relationship between the voltage drop across it ![]() and the rate of change of the current that passes through it
and the rate of change of the current that passes through it ![]() :
:
![]()
Where ![]() is the constant of proportionality, namely the inductance. When the elements are combined, ODEs are generated with
is the constant of proportionality, namely the inductance. When the elements are combined, ODEs are generated with ![]() being the independent variable, and
being the independent variable, and ![]() and
and ![]() being the dependent variables.
being the dependent variables.
Classification of ODEs
Order
The order of an ODE is the order of the highest derivative appearing in the equation. For example, the following equation (Newton’s equation) is a second-order ODE:
![]()
while the beam equation is a fourth-order ODE:
![]()
Linear vs. Nonlinear
An ODE is linear if it can be written as the linear combination:
![]()
where ![]() and
and ![]() are functions of the independent variable
are functions of the independent variable ![]() . All the examples above are considered linear ODEs.
. All the examples above are considered linear ODEs.
The following are two examples of nonlinear ODEs with ![]() being the dependent variable and
being the dependent variable and ![]() being the independent variable:
being the independent variable:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\mathrm{d}x}{\mathrm{d}t}&=\frac{k}{x}\\ \frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=\sin{x} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-074c003626a95ffdb5b0971c51bdf454_l3.png)
Homogeneous vs. Nonhomogeneous
A homogeneous ODE is an equation whose every term contains either the dependent variable or one of its derivatives. For example, Newton’s second law applied to a spring without the gravitational term is a linear homogeneous ODE:
![]()
If one of the non-zero terms in the ODE contains neither the dependent variable nor any of its derivatives, the equation is nonhomogeneous. As an example, if the gravitational term is added to Newton’s second law, then, the equation becomes nonhomogeneous:
![]()
The free term (the term devoid of the dependent variables and any of its derivatives) is called the source term.
A linear homogeneous ODE has the following form:
![]()
while a linear nonhomogeneous ODE has the form:
![]()
The term ![]() is called the source term. The solution to a linear homogeneous equation is called the complementary solution
is called the source term. The solution to a linear homogeneous equation is called the complementary solution ![]() while the solution when a source term appears in the equation is the sum of the complementary solution
while the solution when a source term appears in the equation is the sum of the complementary solution ![]() and the particular solution
and the particular solution ![]() (which is particular to the source term
(which is particular to the source term ![]() ). For example, the solution to Newton’s second law without the gravitational term has the form:
). For example, the solution to Newton’s second law without the gravitational term has the form:
![]()
while the solution when the gravitational term appears has the form:
![]()
The particular solution is the term ![]() .
.
IVP vs. BVP
Depending on the boundary conditions, an ODE can be classified as either an Initial Value Problem (IVP) or a Boundary Value Problem (BVP). An initial value problem is an ODE given with initial conditions of the dependent variable and its derivative at a particular value of the independent variable. This usually applies to dynamic systems whose independent variable is time. For example, Newton’s second law of motion is an initial value problem because the initial value at ![]() of the displacement
of the displacement ![]() and the velocity
and the velocity ![]() are required to reach a solution. The initial values lead to a particular path that is a function of time
are required to reach a solution. The initial values lead to a particular path that is a function of time ![]() .
.
A boundary value problem is an ODE given with boundary conditions at different points. This usually applies to static systems whose independent variable is position. For example, the Euler-Bernoulli beam deflection equation is a boundary value problem. The boundary conditions of the displacement ![]() , the rotation
, the rotation ![]() , and the third and fourth derivatives, are usually given at boundary points on the beam which will then dictate the equilibrium deflection of the beam as a function of position
, and the third and fourth derivatives, are usually given at boundary points on the beam which will then dictate the equilibrium deflection of the beam as a function of position ![]() .
.
Solution Methods for IVPs
(Explicit) Euler Method
The Euler method is one of the simplest methods for solving first-order IVPs. Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, we can use a Taylor approximation to estimate the value of
, then, we can use a Taylor approximation to estimate the value of ![]() at
at ![]() , namely
, namely ![]() with
with ![]() :
:
![]()
Substituting the differential equation into the above equation yields:
![]()
Therefore, as an approximation, an estimate for ![]() can be taken as
can be taken as ![]() as follows:
as follows:
![]()
Using this estimate, the local truncation error is thus proportional to the square of the step size with the constant of proportionality related to the second derivative of ![]() , which is the first derivative of the given IVP:
, which is the first derivative of the given IVP:
![]()
If the errors from each interval are added together, with ![]() being the number of intervals and
being the number of intervals and ![]() the total length
the total length ![]() , then, the total error is:
, then, the total error is:
![]()
There are many examples in engineering and biology in which such IVPs appear. Check this page for examples.
The following Mathematica code provides a procedure whose inputs are
- The differential equation as a function of the dependent variable
 and the independent variable
and the independent variable 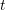 .
. - The step size
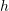 .
. - The initial value
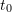 and the final value
and the final value  of the independent variable.
of the independent variable. - The initial value
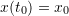 .
.
The procedure then carries on the Euler method and outputs the required data vector.
View Mathematica Code
EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
function1[y_, t_] := 0.05 y
function2[x_, t_] := 0.015 x
EulerMethod[function1, 35, 1.0, 0, 50] // MatrixForm
EulerMethod[function2, 35, 1.0, 0, 50] // MatrixForm
Example 1
The Canadian population at ![]() (current year) is 35 million. If 2.5% of the population have a child in a given year, while the death rate is 1% of the population, what will the population be in 50 years? What if 6% of the population have a child in a given year and the death rate is kept constant at 1%, what will the population be in 50 years?
(current year) is 35 million. If 2.5% of the population have a child in a given year, while the death rate is 1% of the population, what will the population be in 50 years? What if 6% of the population have a child in a given year and the death rate is kept constant at 1%, what will the population be in 50 years?
Solution
The rate of growth is directly proportional to the current population with the constant of proportionality ![]() . If
. If ![]() represents the population in millions and
represents the population in millions and ![]() represents the time in years, then the IVP is given by:
represents the time in years, then the IVP is given by:
![]()
With the initial condition of ![]() , the exact solution to this differential equation is:
, the exact solution to this differential equation is:
![]()
If the birth rate is 6%, then ![]() and the exact solution of the population follows the following equation:
and the exact solution of the population follows the following equation:
![]()
The Euler method provides a numerical solution as follows. Using a step size of ![]() , we can set
, we can set ![]() years. The value of
years. The value of ![]() is given as 35 million. When
is given as 35 million. When ![]() , the value of
, the value of ![]() in millions is given by:
in millions is given by:
![]()
The value of ![]() is given by:
is given by:
![]()
Iterating further, the values of ![]() at each time point can be obtained. The following is the Microsoft Excel table showing the values of
at each time point can be obtained. The following is the Microsoft Excel table showing the values of ![]() in years and the corresponding values of the population
in years and the corresponding values of the population ![]() in millions:
in millions:
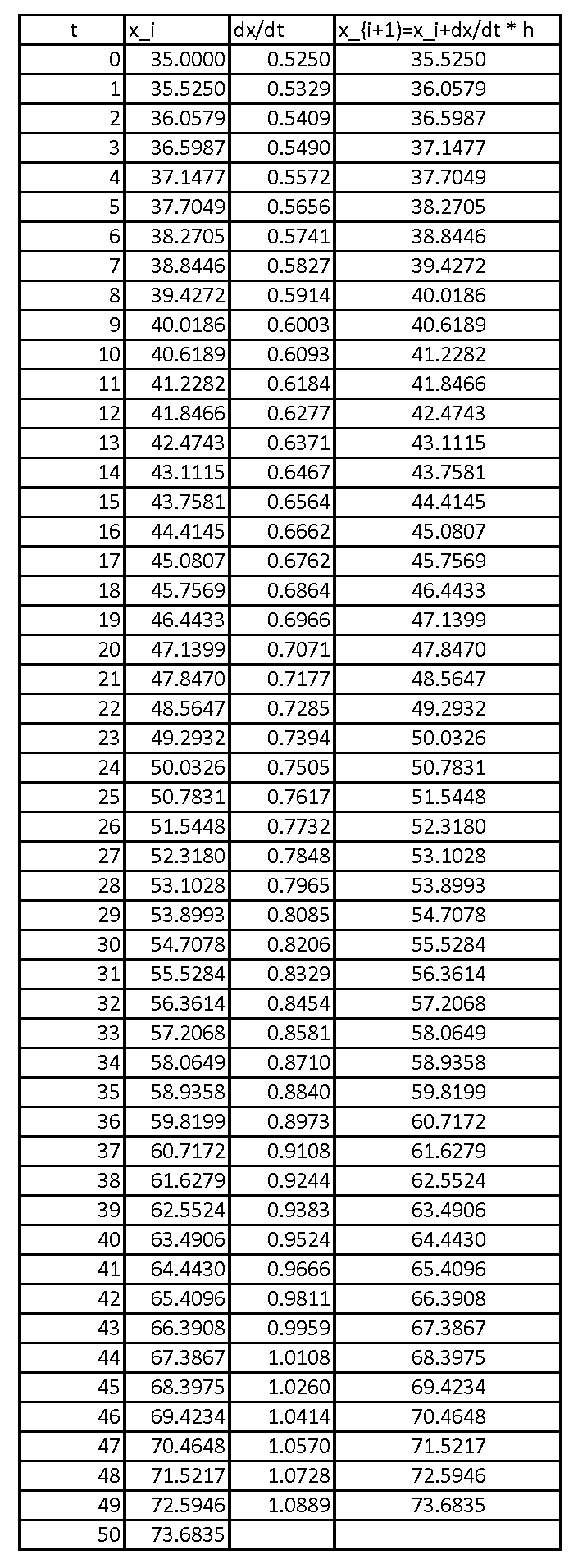
When ![]() , the numerical procedure produces a very good approximation for the population at
, the numerical procedure produces a very good approximation for the population at ![]() years. The error between the prediction of the exact solution to the differential equation and the numerical value at
years. The error between the prediction of the exact solution to the differential equation and the numerical value at ![]() is given in millions by:
is given in millions by:
![]()
The relative error in this case is given by:
![]()
For the second case, when ![]() , the value of
, the value of ![]() in millions is given by:
in millions is given by:
![]()
Proceeding iteratively, the following is the Microsoft Excel table showing the values of ![]() in years and the corresponding values of the population
in years and the corresponding values of the population ![]() in millions:
in millions:
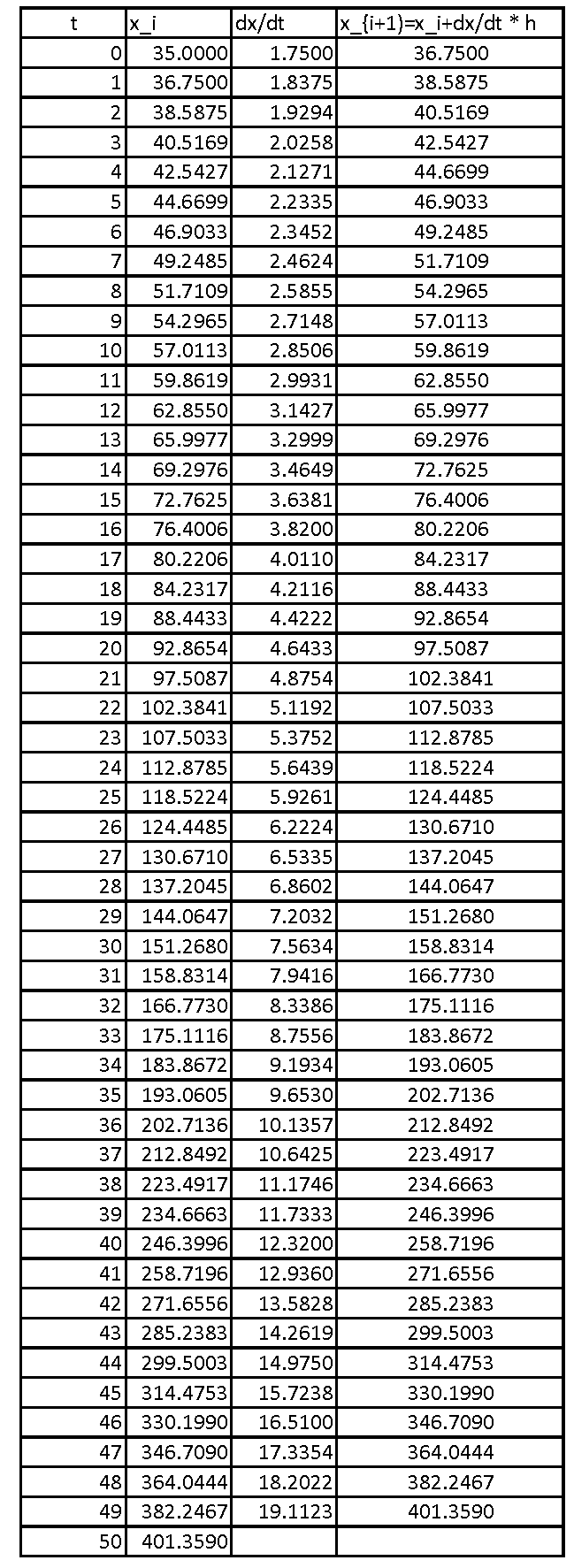
Compared to the previous case, when ![]() , the numerical procedure is not as good. The error between the prediction of the exact solution to the differential equation and the numerical value at
, the numerical procedure is not as good. The error between the prediction of the exact solution to the differential equation and the numerical value at ![]() is given in millions by:
is given in millions by:
![]()
The relative error in this case is given by:
![]()
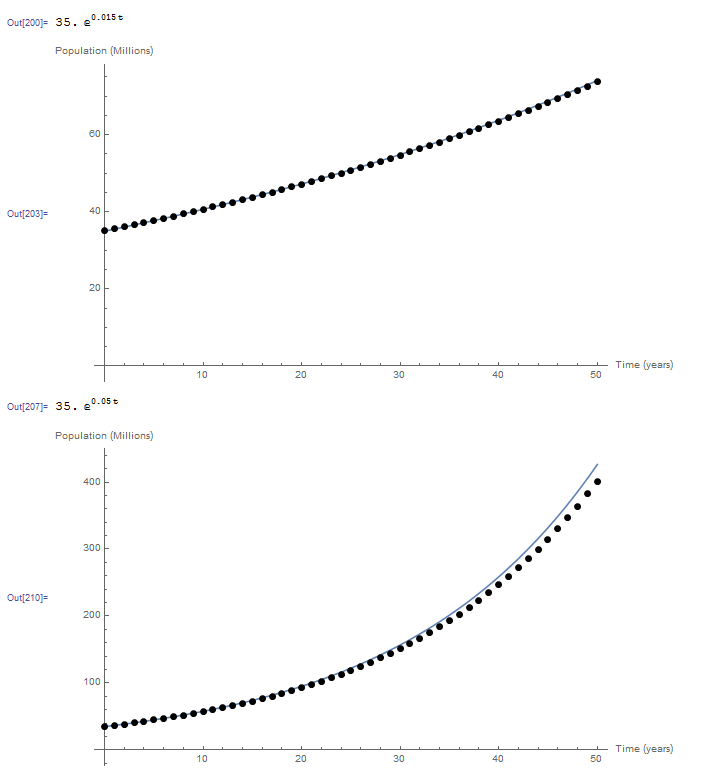
The following is the graph showing the exact solution versus the data using the Euler method for both cases. The Mathematica code used is given below. Notice how the error in the Euler method increases as ![]() increases.
increases.
View Mathematica Code
EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
Clear[x, xtable]
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
Clear[x, xtable]
k = 0.05;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
The following tool illustrates the effect of choosing the step size ![]() on the difference between the numerical solution (shown as dots) and the exact solution (shown as the blue curve) for the case when
on the difference between the numerical solution (shown as dots) and the exact solution (shown as the blue curve) for the case when ![]() . The smaller the step size, the more accurate the solution is. The higher the value of
. The smaller the step size, the more accurate the solution is. The higher the value of ![]() , the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
, the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
Example 2
This example is adopted from this page. A lake of volume ![]() has an initial concentration of a particular pollutant of
has an initial concentration of a particular pollutant of ![]() parts per billion (ppb). This pollutant is due to a pesticide that is no longer available in the market. The volume of the lake is constant throughout the year, with daily water flowing into and out of the lake at the rate of
parts per billion (ppb). This pollutant is due to a pesticide that is no longer available in the market. The volume of the lake is constant throughout the year, with daily water flowing into and out of the lake at the rate of ![]() . As the pesticide is no longer used, the concentration of the pollutant in the surrounding soil is given in ppb as a function of
. As the pesticide is no longer used, the concentration of the pollutant in the surrounding soil is given in ppb as a function of ![]() (days) by
(days) by ![]() which indicates that the concentration is following an exponential decay. This concentration can be assumed to be that of the pollutant in the fluid flowing into the lake. The concentration of the pollutant in the fluid flowing out of the lake is the same as the concentration in the lake. What is the concentration of this particular pollutant in the lake after two years?
which indicates that the concentration is following an exponential decay. This concentration can be assumed to be that of the pollutant in the fluid flowing into the lake. The concentration of the pollutant in the fluid flowing out of the lake is the same as the concentration in the lake. What is the concentration of this particular pollutant in the lake after two years?
Solution
The first step in this problem is to properly write the differential equation that needs to be solved. If ![]() is the total amount of pollutant in the lake, then, the rate of change of
is the total amount of pollutant in the lake, then, the rate of change of ![]() with respect to
with respect to ![]() is equal to the total amount of pollutant entering into the lake per day. Each day, the total amount of pollutant entering the lake is given by
is equal to the total amount of pollutant entering into the lake per day. Each day, the total amount of pollutant entering the lake is given by ![]() , while the total amount of pollutant exiting the lake is given by
, while the total amount of pollutant exiting the lake is given by ![]() . Therefore:
. Therefore:
![]()
The concentration is equal to the total amount divided by the volume of the lake, therefore, the differential equation in terms of ![]() is given by:
is given by:
![]()
Notice that finding an exact solution to the above differential equation is not an easy task and a numerical solution would be the preferred solution in this case. Taking ![]() day,
day, ![]() , and
, and ![]() ppb the Euler method can be used to find the concentration at
ppb the Euler method can be used to find the concentration at ![]() days. You can download the Microsoft Excel file example2.xlsx showing the calculations and the produced graph.
days. You can download the Microsoft Excel file example2.xlsx showing the calculations and the produced graph.
Taking ![]() day, we will show the calculations for the estimates
day, we will show the calculations for the estimates ![]() and
and ![]() . At
. At ![]() day:
day:
![Rendered by QuickLaTeX.com \[\begin{split} c_1&=c_0+h\frac{\mathrm{d}c}{\mathrm{d}t}\bigg|_{c=c_0,t=t_0}\\ &=5+1\left(\frac{\left(100+50\cos{(2\pi 0/365)}\right)}{10000}\left(5e^{\left(\frac{-2(0)}{1000}\right)}-5\right)\right)\\ &=5 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-16d2198efd90a4abcf54c2d749d319ae_l3.png)
At ![]() days:
days:
![Rendered by QuickLaTeX.com \[\begin{split} c_2&=c_1+h\frac{\mathrm{d}c}{\mathrm{d}t}\bigg|_{c=c_1,t=t_1}\\ &=5+1\left(\frac{\left(100+50\cos{(2\pi 1/365)}\right)}{10000}\left(5e^{\left(\frac{-2(1)}{1000}\right)}-5\right)\right)\\ &=4.9999 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e7e399e2f9191c1359d042638b1d0ee7_l3.png)
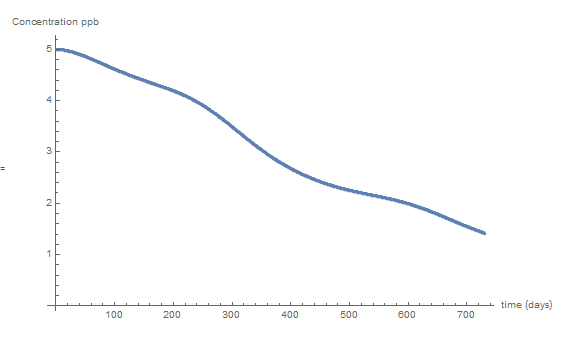
Carrying on produces the values of ![]() at the remaining time intervals up to
at the remaining time intervals up to ![]() days. The following is the output produced by the Mathematica code below.
days. The following is the output produced by the Mathematica code below.
EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
f[t_] := 100 + 50*Cos[2 Pi*t/365];
cin[t_] := 5 E^(-2 t/1000);
fp[c_, t_] := f[t] (cin[t] - c)/10000;
Data = EulerMethod[fp, 5, 1.0, 0, 365*2];
ListPlot[Data, AxesLabel -> {"time (days)", "Concentration ppb"}]
Example 3
In this example we investigate the issue of stability of numerical solution of differential equations using the Euler method. Consider the IVP of the form:
![]()
If ![]() , compare the two solutions taking a step size of
, compare the two solutions taking a step size of ![]() , and a step size of
, and a step size of ![]() .
.
Solution
The exact solution to the given equation is given by:
![]()
Using an explicit Euler scheme, the value of ![]() can be obtained as follows:
can be obtained as follows:
![]()
Therefore:
![]()
When ![]() , the term
, the term ![]() is bounded for any value of
is bounded for any value of ![]() which means that the value of
which means that the value of ![]() is always bounded. However, if
is always bounded. However, if ![]() , then, the term
, then, the term ![]() oscillates wildly leading to an instability in the numerical scheme!
oscillates wildly leading to an instability in the numerical scheme!
The following tool illustrates the difference between the obtained result for ![]() . Vary the value of
. Vary the value of ![]() and try to identify the point above which the obtained solution (black dots) starts oscillating wildly around the exact solution (blue curve).
and try to identify the point above which the obtained solution (black dots) starts oscillating wildly around the exact solution (blue curve).
Backward (Implicit) Euler Method
Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, we can use a Taylor approximation to relate the value of
, then, we can use a Taylor approximation to relate the value of ![]() at
at ![]() , namely
, namely ![]() with
with ![]() . However, unlike the explicit Euler method, we will use the Taylor series around the point
. However, unlike the explicit Euler method, we will use the Taylor series around the point ![]() , that is:
, that is:
![]()
Substituting the differential equation into the above equation yields:
![]()
Therefore, as an approximation, an estimate for ![]() can be taken as
can be taken as ![]() as follows:
as follows:
![]()
Using this estimate, the local truncation error is thus proportional to the square of the step size with the constant of proportionality related to the second derivative of ![]() , which is the first derivative of the given IVP. The backward Euler method is termed an “implicit” method because it uses the slope
, which is the first derivative of the given IVP. The backward Euler method is termed an “implicit” method because it uses the slope ![]() at the unknown point
at the unknown point ![]() , namely:
, namely: ![]() . The developed equation can be linear in
. The developed equation can be linear in ![]() or nonlinear. Nonlinear equations can often be solved using the fixed-point iteration method or the Newton-Raphson method to find the value of
or nonlinear. Nonlinear equations can often be solved using the fixed-point iteration method or the Newton-Raphson method to find the value of ![]() . While the implicit scheme does not provide better accuracy than the explicit scheme, it comes with additional computations. However, one advantage is that this scheme is always stable.
. While the implicit scheme does not provide better accuracy than the explicit scheme, it comes with additional computations. However, one advantage is that this scheme is always stable.
The following Mathematica code adopts the implicit Euler scheme and uses the built-in FindRoot function to solve for ![]() . The code is similar to the code provided for the explicit scheme except for the line to calculate
. The code is similar to the code provided for the explicit scheme except for the line to calculate ![]() .
.
View Mathematica Code
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[ s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
function1[y_, t_] := 0.05 y
function2[x_, t_] := 0.015 x
ImplicitEulerMethod[function1, 35, 1.0, 0, 50] // MatrixForm
ImplicitEulerMethod[function2, 35, 1.0, 0, 50] // MatrixForm
Example 1
Repeat Example 1 above using the implicit Euler method.
Solution
When ![]() , the IVP is given by:
, the IVP is given by:
![]()
Given a value for ![]() at
at ![]() , and taking
, and taking ![]() , the estimate for
, the estimate for ![]() can be calculated according to the formula:
can be calculated according to the formula:
![]()
Rearranging yields:
![]()
With ![]() million and
million and ![]() years, the estimate for the population at
years, the estimate for the population at ![]() years using the implicit Euler method is given by:
years using the implicit Euler method is given by:
![]()
at ![]() years, the value of
years, the value of ![]() in millions is given by:
in millions is given by:
![]()
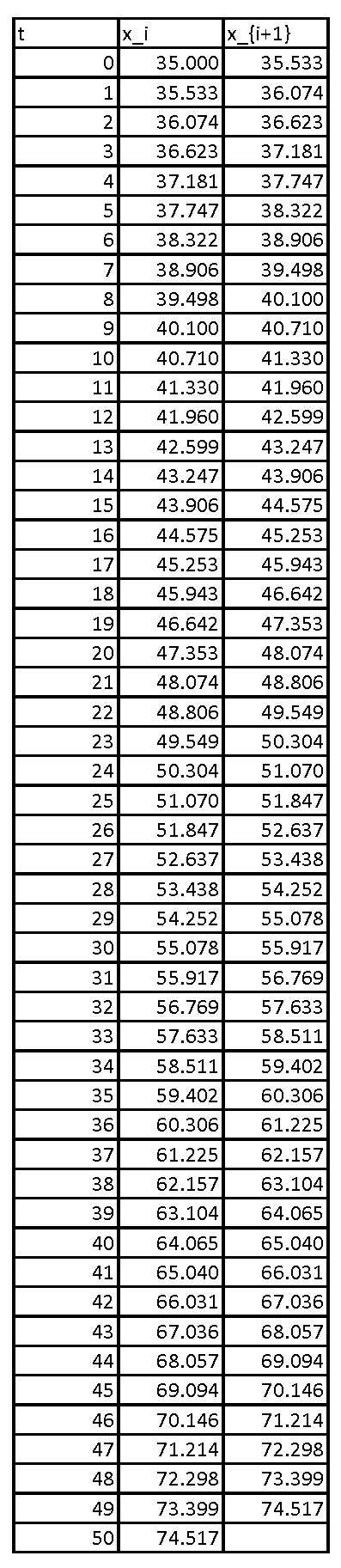
Proceeding iteratively, the following is the Excel table showing the values of the population up to ![]() years.
years.
When ![]() , the implicit method provides an error similar to that of the explicit method:
, the implicit method provides an error similar to that of the explicit method:
![Rendered by QuickLaTeX.com \[\begin{split} E&=35e^{(0.015\times 50)}-74.517=74.095-74.517=-0.4\\ E_r&=\frac{-0.4}{74.095}=-0.005 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f8a23099f5c25fc75f56564f35bb9588_l3.png)
When ![]() , the IVP is given by:
, the IVP is given by:
![]()
Given a value for ![]() at
at ![]() , and taking
, and taking ![]() , the estimate for
, the estimate for ![]() can be calculated according to the formula:
can be calculated according to the formula:
![]()
Rearranging yields:
![]()
With ![]() million and
million and ![]() years, the estimate for the population at
years, the estimate for the population at ![]() years using the implicit Euler method is given by:
years using the implicit Euler method is given by:
![]()
at ![]() years, the value of
years, the value of ![]() in millions is given by:
in millions is given by:
![]()
Proceeding iteratively, the following is the Excel table showing the values of the population up to ![]() years.
years.
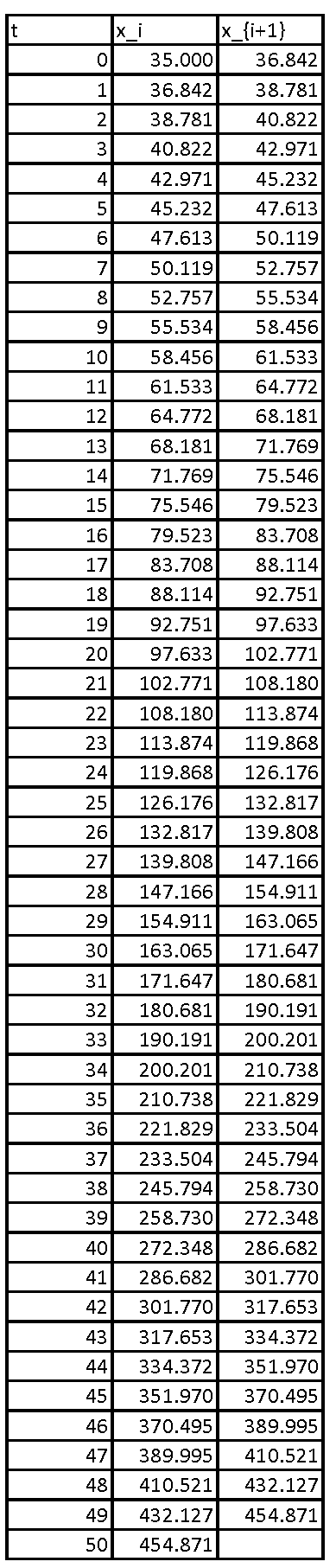
Again, the error produced by the implicit method is comparable to that produced by the explicit method shown above:
![Rendered by QuickLaTeX.com \[\begin{split} E&=35e^{(0.05\times 50)}-454.871=426.387-454.871=-28.483\\ E_r&=\frac{-28.483}{426.387}=-0.07 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c0441ba8f79923f56a1dcc838436368e_l3.png)
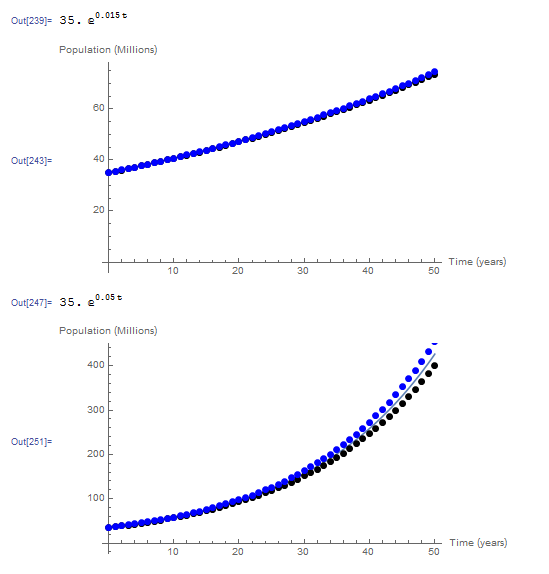
The following is the graph showing the exact solution versus the data using both the implicit (blue dots) and the explicit (black dots) Euler method for both values of ![]() .
.
View Mathematica Code
EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Data2 = ImplicitEulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data], Blue, Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
Clear[x, xtable]
k = 0.05;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Data2 = ImplicitEulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data], Blue, Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
The following tool illustrates the effect of choosing the step size ![]() on the difference between the numerical solution obtained using the implicit methods (shown as dots) and the exact solution (shown as the blue curve) for the case when
on the difference between the numerical solution obtained using the implicit methods (shown as dots) and the exact solution (shown as the blue curve) for the case when ![]() . The smaller the step size, the more accurate the solution is. The higher the value of
. The smaller the step size, the more accurate the solution is. The higher the value of ![]() , the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
, the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
Example 2
Repeat Example 2 above using the implicit Euler method.
Solution
Recall that the IVP for this problem is given by:
![]()
Taking ![]() day,
day, ![]() can be predicted for a given value of
can be predicted for a given value of ![]() using the implicit Euler method as follows:
using the implicit Euler method as follows:
![]()
Rearranging:
![Rendered by QuickLaTeX.com \[ c_{i+1}=\frac{c_i+\frac{\left(100+50\cos{(2\pi t_{i+1}/365)}\right)}{10000}\left(5e^{\left(\frac{-2t_{i+1}}{1000}\right)}\right)}{1+\frac{\left(100+50\cos{(2\pi t_{i+1}/365)}\right)}{10000}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e611ae4dcaa1909494de0a6acecca246_l3.png)
With ![]() and
and ![]() ppb,
ppb, ![]() is calculated as:
is calculated as:
![Rendered by QuickLaTeX.com \[ c_1=\frac{5+0.015\left(5e^{\left(\frac{-2(1)}{1000}\right)}\right)}{1+0.015}=4.9999 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-294d3816e7abfd1b4e50168dd35b9d11_l3.png)
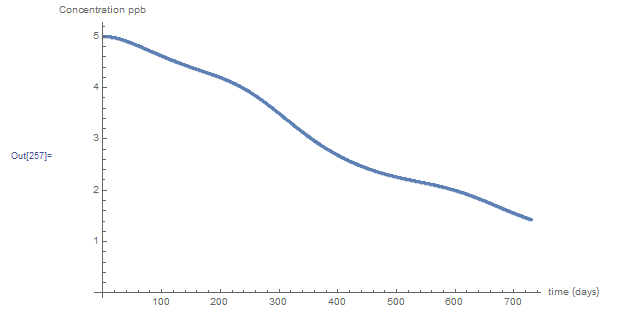
Proceeding iteratively produces the following graph with results almost identical to those produced by the explicit method. You can download the Microsoft Excel file example2implicit.xlsx showing the calculations.
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
f[t_] := 100 + 50*Cos[2 Pi*t/365];
cin[t_] := 5 E^(-2 t/1000);
fp[c_, t_] := f[t] (cin[t] - c)/10000;
Data = ImplicitEulerMethod[fp, 5, 1, 0, 365*2];
ListPlot[Data, AxesLabel -> {"time (days)", "Concentration ppb"}]
Example 3
We will repeat Example 3 above to illustrate that the implicit Euler method is always stable.
Consider the IVP of the form:
![]()
If ![]() , compare the two solutions taking a step size of
, compare the two solutions taking a step size of ![]() , and a step size of
, and a step size of ![]() .
.
Solution
Using an implicit Euler scheme, the value of ![]() can be obtained as follows:
can be obtained as follows:
![]()
Therefore:
![]()
![]() is a positive number. Therefore, the term
is a positive number. Therefore, the term ![]() is bounded for every
is bounded for every ![]() and therefore,
and therefore, ![]() is bounded. The following tool illustrates the difference between the obtained result for
is bounded. The following tool illustrates the difference between the obtained result for ![]() . Vary the value of
. Vary the value of ![]() and notice how the obtained solution (black dots) compares to the exact solution (blue curve). While the accuracy is lost with higher values of
and notice how the obtained solution (black dots) compares to the exact solution (blue curve). While the accuracy is lost with higher values of ![]() , the solution maintains numerical stability.
, the solution maintains numerical stability.
Example 4
Consider the following nonlinear IVP:
![]()
with the initial condition ![]() . Find the values of
. Find the values of ![]() for
for ![]() taking
taking ![]() using the implicit Euler method.
using the implicit Euler method.
Solution
Using Mathematica, the exact solution to the differential equation given can be obtained as:
![]()
The implicit Euler scheme provides the following estimate for ![]() :
:
![]()
Since ![]() appears on both sides, and the equation is nonlinear in
appears on both sides, and the equation is nonlinear in ![]() , therefore, the Newton-Raphson method will be used at each time increment to find the value of
, therefore, the Newton-Raphson method will be used at each time increment to find the value of ![]() !
!
Setting ![]() ,
, ![]() ,
, ![]() , and
, and ![]() yields:
yields:
![]()
Solving the above nonlinear equation in ![]() using the Newton-Raphson method yields:
using the Newton-Raphson method yields:
![]()
Similarly, with ![]() , the equation for
, the equation for ![]() is:
is:
![]()
Using the Newton-Raphson method:
![]()
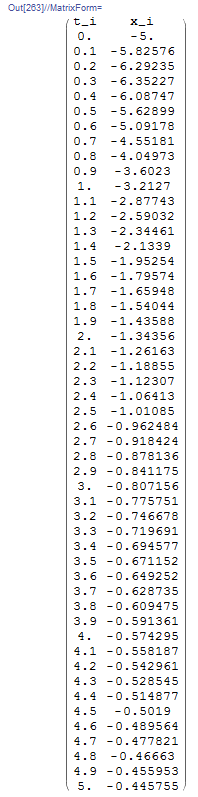
Proceeding iteratively produces the following table:
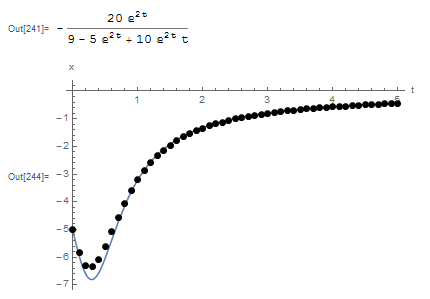
The following is the plot of the exact solution (blue line) with the data obtained using the implicit Euler method. The Mathematica code is given below.
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = ImplicitEulerMethod[fp, -5.0, 0.1, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]},AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
Heun’s Method
Heun’s method provides a slight modification to both the implicit and explicit Euler methods. Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, we have:
, then, we have:
![]()
Therefore:
![]()
If the trapezoidal rule is used for the right-hand side with one interval we obtain:
![]()
where the error term is inherited from the use of the trapezoidal integration rule. Therefore an estimate for ![]() is given by:
is given by:
![]()
Using this estimate, the local truncation error is thus proportional to the cube of the step size. If the errors from each interval are added together, with ![]() being the number of intervals and
being the number of intervals and ![]() the total length
the total length ![]() , then, the total error is:
, then, the total error is:
![]()
which is better than both the implicit and explicit Euler methods. Note that Heun’s method is essentially a slight modification to the Euler’s method in which the slope used to calculate the value of ![]() at the next time point is used as the average slope at
at the next time point is used as the average slope at ![]() and at
and at ![]() . Heun’s method can be implemented in two ways. One way is to use the slope at
. Heun’s method can be implemented in two ways. One way is to use the slope at ![]() to calculate an initial estimate
to calculate an initial estimate ![]() . Then, the estimate for
. Then, the estimate for ![]() would be calculated based on the slopes at
would be calculated based on the slopes at ![]() and
and ![]() . Alternatively, the Newton-Raphson method or the fixed-point iteration method can be used to solve directly for
. Alternatively, the Newton-Raphson method or the fixed-point iteration method can be used to solve directly for ![]() . We will only adopt the first way. The following Mathematica code presents a procedure to utilize Heun’s method. The procedure is essentially similar to the ones presented in the Euler methods except for the step to calculate the new estimate
. We will only adopt the first way. The following Mathematica code presents a procedure to utilize Heun’s method. The procedure is essentially similar to the ones presented in the Euler methods except for the step to calculate the new estimate ![]() .
.
View Mathematica Code
HeunMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xi0 = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h];
xtable[[i]] = xtable[[i - 1]] + h (fp[xtable[[i - 1]], t0 + (i - 2) h] +fp[xi0, t0 + (i - 1) h])/2, {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
Example
Solve Example 4 above using Heun’s method.
Solution
Heun’s method is implemented by first assuming an estimate for ![]() based on the explicit Euler method:
based on the explicit Euler method:
![]()
Then, the estimate for ![]() is calculated as:
is calculated as:
![Rendered by QuickLaTeX.com \[ x_{i+1}=x_i+h\frac{\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_{i+1}^{(0)},t=t_{i+1}}+\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_{i},t=t_{i}}}{2} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-81f45c540552d63c8f74ce02bb324351_l3.png)
Setting ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , an initial estimate for
, an initial estimate for ![]() is given by:
is given by:
![]()
Using this information, the slope at ![]() can be calculated and used to estimate
can be calculated and used to estimate ![]() :
:
![]()
Similarly, an initial estimate for ![]() is given by:
is given by:
![]()
Using this information, the slope at ![]() can be calculated and used to estimate
can be calculated and used to estimate ![]() :
:
![]()
Proceeding iteratively gives the values of ![]() up to
up to ![]() . The Microsoft Excel file Heun.xlsx provides the required calculations.
. The Microsoft Excel file Heun.xlsx provides the required calculations.
The following graph shows the produced numerical data (black dots) overlapping the exact solution (blue line). The Mathematica code is given below.
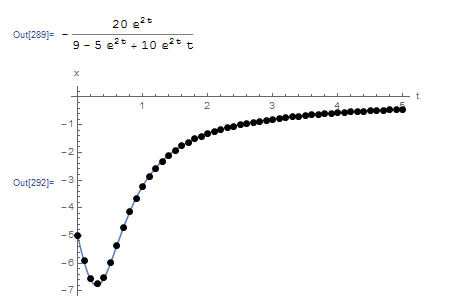
HeunMethod[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xi0 = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h];
xtable[[i]] = xtable[[i - 1]] + h (fp[xtable[[i - 1]], t0 + (i - 2) h] + fp[xi0, t0 + (i - 1) h])/2, {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = HeunMethod[fp, -5.0, 0.1, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
The following tool provides a comparison between the explicit Euler method and Heun’s method. Notice that around ![]() , the function
, the function ![]() varies highly in comparison to the rest of the domain. The biggest difference between Heun’s method and the Euler method can be seen when
varies highly in comparison to the rest of the domain. The biggest difference between Heun’s method and the Euler method can be seen when ![]() around this area. Heun’s method is able to trace the curve while the Euler method has higher deviations.
around this area. Heun’s method is able to trace the curve while the Euler method has higher deviations.
The Midpoint Method
Similar to Heun’s method, the midpoint method provides a slight modification to both the implicit and explicit Euler methods. Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, we have:
, then, we have:
![]()
Therefore:
![]()
If the midpoint rule of the rectangle method of numerical integration is used for the right-hand side with one interval we obtain:
![]()
where the error term is inherited from the use of ![]() in the rectangle rule. Therefore an estimate for
in the rectangle rule. Therefore an estimate for ![]() is given by:
is given by:
![]()
Using this estimate, the local truncation error is thus proportional to the cube of the step size. If the errors from each interval are added together, with ![]() being the number of intervals and
being the number of intervals and ![]() the total length
the total length ![]() , then, the total error is:
, then, the total error is:
![]()
which is similar to Heun’s method but better than both the implicit and explicit Euler methods. Note that the midpoint method is essentially a slight modification to the Euler’s method in which the slope used to calculate the value of ![]() at the next time point is used as the slope at the average point
at the next time point is used as the slope at the average point ![]() . The midpoint method can be implemented in two ways. One way is to use the slope at
. The midpoint method can be implemented in two ways. One way is to use the slope at ![]() to calculate an initial estimate
to calculate an initial estimate ![]() . Then, the estimate for
. Then, the estimate for ![]() would be calculated based on the slope at
would be calculated based on the slope at ![]() . Alternatively, the Newton-Raphson method or the fixed-point iteration method can be used to solve directly for
. Alternatively, the Newton-Raphson method or the fixed-point iteration method can be used to solve directly for ![]() . We will only adopt the first way. The following Mathematica code presents a procedure to utilize the midpoint method. The procedure is essentially similar to the ones presented in the Euler methods except for the step to calculate the new estimate
. We will only adopt the first way. The following Mathematica code presents a procedure to utilize the midpoint method. The procedure is essentially similar to the ones presented in the Euler methods except for the step to calculate the new estimate ![]() .
.
View Mathematica Code
MidPointMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xi120 = xtable[[i - 1]] + h/2*fp[xtable[[i - 1]], t0 + (i - 2) h];
xtable[[i]] = xtable[[i - 1]] + h (fp[xi120, t0 + (i - 1-1/2) h]), {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
Example
Solve Example 4 above using the midpoint method.
Solution
The midpoint method is implemented by first assuming an estimate for ![]() based on the explicit Euler method:
based on the explicit Euler method:
![]()
Then, the estimate for ![]() is calculated as:
is calculated as:
![]()
Setting ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , an initial estimate for
, an initial estimate for ![]() is given by:
is given by:
![]()
Using this information, the slope at ![]() can be calculated and used to estimate
can be calculated and used to estimate ![]() :
:
![]()
Similarly, an initial estimate for ![]() is given by:
is given by:
![]()
Using this information, the slope at ![]() can be calculated and used to estimate
can be calculated and used to estimate ![]() :
:
![]()
Proceeding iteratively gives the values of ![]() up to
up to ![]() . The Microsoft Excel file MidPoint.xlsx provides the required calculations.
. The Microsoft Excel file MidPoint.xlsx provides the required calculations.
The following graph shows the produced numerical data (black dots) overlapping the exact solution (blue line). The Mathematica code is given below.
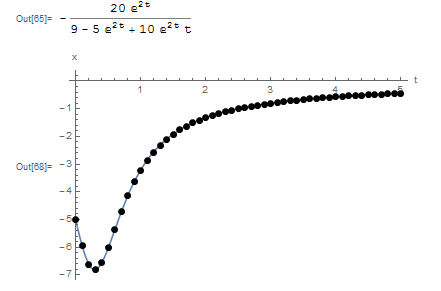
MidPointMethod[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xi120 = xtable[[i - 1]] + h/2*fp[xtable[[i - 1]], t0 + (i - 2) h];
xtable[[i]] = xtable[[i - 1]] + h (fp[xi120, t0 + (i - 1 - 1/2) h]), {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = MidPointMethod[fp, -5.0, 0.1, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
The following tool provides a comparison between the explicit Euler method and the midpoint method. The midpoint method behaves very similar to Heun’s method. Notice that around ![]() , the function
, the function ![]() varies highly in comparison to the rest of the domain. The biggest difference between midpoint method and the Euler method can be seen when
varies highly in comparison to the rest of the domain. The biggest difference between midpoint method and the Euler method can be seen when ![]() around this area. The midpoint method is able to trace the curve while the Euler method has higher deviations.
around this area. The midpoint method is able to trace the curve while the Euler method has higher deviations.
Runge-Kutta Methods
The Runge-Kutta methods developed by the German mathematicians C. Runge and M.W. Kutta are essentially a generalization of all the previous methods. Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, the Runge-Kutta methods employ the following general equation to calculate the value of
, then, the Runge-Kutta methods employ the following general equation to calculate the value of ![]() at
at ![]() , namely
, namely ![]() with
with ![]() :
:
![]()
where ![]() is a function of the form:
is a function of the form:
![]()
![]() are constants while
are constants while ![]() evaluated at points within the interval
evaluated at points within the interval ![]() and have the form:
and have the form:
![Rendered by QuickLaTeX.com \[\begin{split} k_1&=F(x_i,t_i)\\ k_2&=F(x_i+q_{11}k_1h,t_i+p_1h)\\ k_3&=F(x_i+q_{21}k_1h+q_{22}k_2h,t_i+p_2h)\\ &\vdots\\ k_n&=F(x_i+q_{(n-1),1}k_1h+q_{(n-1),2}k_2h+\cdots+q_{(n-1),(n-1)}k_{n-1}h,t_i+p_{n-1}h) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0857e00462c2a64a7c822e3a3aa89472_l3.png)
The constants ![]() , and the forms of
, and the forms of ![]() are obtained by equating the value of
are obtained by equating the value of ![]() obtained using the Runge-Kutta equation to a particular form of the Taylor series. The
obtained using the Runge-Kutta equation to a particular form of the Taylor series. The ![]() are recurrence relationships, meaning
are recurrence relationships, meaning ![]() appears in
appears in ![]() , which appears in
, which appears in ![]() , and so forth. This makes the method efficient for computer calculations. The error in a particular form depends on how many terms are used. The general forms of these Runge-Kutta methods could be implicit or explicit. For example, the explicit Euler method is a Runge-Kutta method with only one term with
, and so forth. This makes the method efficient for computer calculations. The error in a particular form depends on how many terms are used. The general forms of these Runge-Kutta methods could be implicit or explicit. For example, the explicit Euler method is a Runge-Kutta method with only one term with ![]() and
and ![]() . Heun’s method on the other hand is a Runge-Kutta method with the following non-zero terms:
. Heun’s method on the other hand is a Runge-Kutta method with the following non-zero terms:
![Rendered by QuickLaTeX.com \[\begin{split} \alpha_1&=\alpha_2=\frac{1}{2}\\ k_1&=F(x_i,t_i)\\ k_2&=F(x_i+hk_1,t_i+h) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1f7d4747d27ae25b527bcea4d694be86_l3.png)
Similarly, the midpoint method is a Runge-Kutta method with the following non-zero terms:
![Rendered by QuickLaTeX.com \[\begin{split} \alpha_2&=1\\ k_1&=F(x_i,t_i)\\ k_2&=F(x_i+\frac{h}{2}k_1,t_i+\frac{h}{2}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ed4c5854d3b69eb19248505f90ce8a21_l3.png)
The most popular Runge-Kutta method is referred to as the “classical Runge-Kutta method”, or the “fourth-order Runge-Kutta method”. It has the following form:
![]()
with
![Rendered by QuickLaTeX.com \[\begin{split} k_1&=F(x_i,t_i)\\ k_2&=F\left(x_i+\frac{h}{2}k_1,t_i+\frac{h}{2}\right)\\ k_3&=F\left(x_i+\frac{h}{2}k_2,t_i+\frac{h}{2}\right)\\ k_4&=F(x_i+hk_3,t_i+h) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-62b75e53ec00694b2456f6c43dc62a80_l3.png)
The error in the fourth-order Runge-Kutta method is similar to that of the Simpson’s 1/3 rule, with a local error term ![]() which would translate into a global error term of
which would translate into a global error term of ![]() . The method is termed fourth-order because the error term is directly proportional to the step size raised to the power of 4.
. The method is termed fourth-order because the error term is directly proportional to the step size raised to the power of 4.
RK4Method[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[k1 = fp[xtable[[i - 1]], t0 + (i - 2) h];
k2 = fp[xtable[[i - 1]] + h/2*k1, t0 + (i - 1.5) h];
k3 = fp[xtable[[i - 1]] + h/2*k2, t0 + (i - 1.5) h];
k4 = fp[xtable[[i - 1]] + h*k3, t0 + (i - 1) h];
xtable[[i]] = xtable[[i - 1]] + h (k1 + 2 k2 + 2 k3 + k4)/6, {i, 2,
n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Example
Solve Example 4 above using the classical Runge-Kutta method but with ![]() .
.
Solution
Recall the differential equation of this problem:
![]()
Setting ![]() ,
, ![]() ,
, ![]() , the following are the values of
, the following are the values of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() required to calculate
required to calculate ![]() :
:
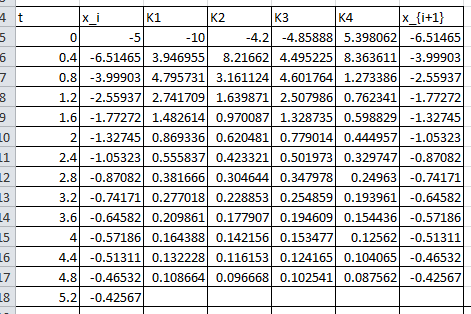
![Rendered by QuickLaTeX.com \[\begin{split} k_1&=F(x_0,t_0)=F(-5,0)\\ &=0+2(-5)=-10\\ k_2&=F\left(x_0+\frac{h}{2}k_1,t_0+\frac{h}{2}\right)=F(-5+0.2(-10),0+0.2)\\ &=0.2(-5+0.2(-10))^2+2\times (-5+0.2(-10))=-4.2\\ k_3&=F\left(x_0+\frac{h}{2}k_2,t_0+\frac{h}{2}\right)=F(-5+0.2(-4.2),0+0.2)\\ &=0.2(-5+0.2(-4.2))^2+2\times (-5+0.2(-4.2))=-4.8589\\ k_4&=F(x_0+hk_3,t_0+h)=F(-5+0.4(-4.8589),0+0.4)\\ &=0.4(-5+0.4(-4.8589))^2+2\times(-5+0.4(-4.8589))=5.3981 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d3c0ff2de7b6c8a09400f4a4ea7a264b_l3.png)
Therefore:
![]()
Proceeding iteratively gives the values of ![]() up to
up to ![]() . The Microsoft Excel file RK4.xlsx provides the required calculations. The following Microsoft Excel table shows the required calculations:
. The Microsoft Excel file RK4.xlsx provides the required calculations. The following Microsoft Excel table shows the required calculations:
The following Mathematica code implements the classical Runge-Kutta method for this problem with ![]() . The output curve is shown underneath.
. The output curve is shown underneath.
View Mathematica Code
RK4Method[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[k1 = fp[xtable[[i - 1]], t0 + (i - 2) h];
k2 = fp[xtable[[i - 1]] + h/2*k1, t0 + (i - 1.5) h];
k3 = fp[xtable[[i - 1]] + h/2*k2, t0 + (i - 1.5) h];
k4 = fp[xtable[[i - 1]] + h*k3, t0 + (i - 1) h];
xtable[[i]] = xtable[[i - 1]] + h (k1 + 2 k2 + 2 k3 + k4)/6, {i, 2,
n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = RK4Method[fp, -5.0, 0.3, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
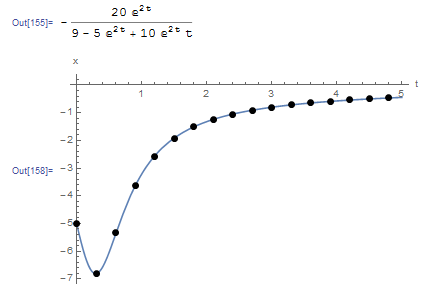
The following tool provides a comparison between the explicit Euler method and the classical Runge-Kutta method. The classical Runge-Kutta method gives excellent predictions even when ![]() , at which point the explicit Euler method fails to predict anything close to the exact equation. The classical Runge-Kutta method also provides better estimates than the midpoint method and Heun’s method above.
, at which point the explicit Euler method fails to predict anything close to the exact equation. The classical Runge-Kutta method also provides better estimates than the midpoint method and Heun’s method above.
Solving Systems of IVPs
Many engineering problems contain systems of IVPs in which more than one dependent variable is a function of one independent variable, say ![]() . For example, chemical reactions of more than one component are usually described using systems of IVPs in which the initial conditions are known. Similarly, the interaction of biological growth of different species (predators and prey) is usually represented by a system of IVPs in which the initial conditions are given. Generally, these systems can be represented as:
. For example, chemical reactions of more than one component are usually described using systems of IVPs in which the initial conditions are known. Similarly, the interaction of biological growth of different species (predators and prey) is usually represented by a system of IVPs in which the initial conditions are given. Generally, these systems can be represented as:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\mathrm{d}x_1}{\mathrm{d}t}&=F_1(x_1,x_2,\cdots,x_n,t)\\ \frac{\mathrm{d}x_2}{\mathrm{d}t}&=F_2(x_1,x_2,\cdots,x_n,t)\\ &\vdots\\ \frac{\mathrm{d}x_n}{\mathrm{d}t}&=F_n(x_1,x_2,\cdots,x_n,t) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c028c330fd24f0e504f2f9955b5e2b53_l3.png)
The independent variable is discretized such that ![]() with a constant step
with a constant step ![]() . In such systems, the initial conditions, namely the values of
. In such systems, the initial conditions, namely the values of ![]() , are given. The values of
, are given. The values of ![]() when
when ![]() are denoted:
are denoted: ![]() . In this case, the values of the dependent variables at
. In this case, the values of the dependent variables at ![]() can be obtained using the following system of equations:
can be obtained using the following system of equations:
![Rendered by QuickLaTeX.com \[ \begin{split} x_1^{(i+1)}&=x_1^{(i)}+\phi_1h\\ x_2^{(i+1)}&=x_2^{(i)}+\phi_2h\\ &\vdots\\ x_n^{(i+1)}&=x_n^{(i)}+\phi_nh\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-41af4495bce87f32917f11df089f0bd0_l3.png)
where ![]() depend on the method used. For example, if the explicit Euler method is used, then:
depend on the method used. For example, if the explicit Euler method is used, then:
![Rendered by QuickLaTeX.com \[ \begin{split} \phi_1&=F_1(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i)\\ \phi_2&=F_2(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i)\\ &\vdots\\ \phi_n&=F_n(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-379da31a947863cacbede79c08ef4abe_l3.png)
Alternatively, if the classical Runge-Kutta method is used, then:
![Rendered by QuickLaTeX.com \[\begin{split} \phi_1&=\frac{1}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\ \phi_2&=\frac{1}{6}(k_{21}+2k_{22}+2k_{23}+k_{24})\\ &\vdots\\ \phi_n&=\frac{1}{6}(k_{n1}+2k_{n2}+2k_{n3}+k_{n4}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-84f8eaa27b952c21a287b7d3e8c95aac_l3.png)
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the
are the ![]() values associated with the dependent variable
values associated with the dependent variable ![]() and calculated according to the classical Runge-Kutta technique.
and calculated according to the classical Runge-Kutta technique.
It should also be noted that higher-order IVPs can be solved by converting them into a system of first-order IVPs. For example, consider the IVP:
![]()
with the initial conditions ![]() and
and ![]() given. Then, setting
given. Then, setting ![]() , the equation can be written as a system of two IVPs:
, the equation can be written as a system of two IVPs:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\mathrm{d}x}{\mathrm{d}t}&=y\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=F(x,t) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-dc83efe352a51f4a101b5a0bbee69d74_l3.png)
with initial conditions given for ![]() and
and ![]() .
.
Example
Consider the damped mechanical system with ![]() ,
, ![]() ,
, ![]() with the initial conditions
with the initial conditions ![]() . Find the numerical solution for the position
. Find the numerical solution for the position ![]() and the velocity
and the velocity ![]() for
for ![]() using the explicit Euler method and the Runge-Kutta method. Use
using the explicit Euler method and the Runge-Kutta method. Use ![]() .
.
Solution
The differential equation of the damped system is given by:
![]()
The following exact solution can be obtained using the built-in DSolve function in Mathematica:
![Rendered by QuickLaTeX.com \[\begin{split} x&=10e^{(-0.075t)}\left(e^{(0.075t)}-\cos{(0.997184t)-0.0752118\sin{(0.997184t)}}\right)\\ x'&=10.0282e^{(-0.075t)}\sin{(0.997184t)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-15864faf5cb725b353a4cc38fe68f037_l3.png)
To find the numerical solution, the equation will be converted into a system of 2 IVPs. Setting ![]() , the equation can be converted into the following system:
, the equation can be converted into the following system:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\mathrm{d}x}{\mathrm{d}t}&=y\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=10-x-0.15y\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-741f03eb7790cccf6d3cc44603526dc4_l3.png)
with the initial conditions ![]() . With
. With ![]() , the interval can be split into
, the interval can be split into ![]() time steps. The time discretization will be such that
time steps. The time discretization will be such that ![]() ,
, ![]() ,
, ![]() , up to
, up to ![]() . The corresponding positions are given by:
. The corresponding positions are given by: ![]() while the corresponding velocities are given by:
while the corresponding velocities are given by: ![]() .
.
Explicit Euler Method
Using the explicit Euler method, the values of ![]() and
and ![]() can be evaluated as:
can be evaluated as:
![Rendered by QuickLaTeX.com \[\begin{split} x_{i+1}&=x_i+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{(x_i,y_i,t_i)}=x_i+hy_i\\ y_{i+1}&=y_i+h\frac{\mathrm{d}y}{\mathrm{d}t}\bigg|_{(x_i,y_i,t_i)}=y_i+h(10-x_i-0.15y_i) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-640b312759be092a5b5f0797da5d399b_l3.png)
With the initial conditions ![]() , the values of
, the values of ![]() and
and ![]() at
at ![]() can be calculated as:
can be calculated as:
![]()
Similarly, the values of ![]() and
and ![]() can be obtained as:
can be obtained as:
![]()
Proceeding iteratively, the values of ![]() and
and ![]() up to
up to ![]() can be obtained. The Microsoft Excel file EulerSystem.xlsx shows the obtained values.
can be obtained. The Microsoft Excel file EulerSystem.xlsx shows the obtained values.
Classical Runge-Kutta method
The two differential equations are designated ![]() and
and ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \[\begin{split} F_1(x,y,t)&=\frac{\mathrm{d}x}{\mathrm{d}t}=y\\ F_2(x,y,t)&=\frac{\mathrm{d}y}{\mathrm{d}t}=10-x-0.15y \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2c2fd21a2e2e68e15eb3029fa8531a20_l3.png)
Using the classical Runge-Kutta method, the values of ![]() and
and ![]() can be evaluated as:
can be evaluated as:
![Rendered by QuickLaTeX.com \[\begin{split} x_{i+1}&=x_i+\frac{h}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\ y_{i+1}&=y_i+\frac{h}{6}(k_{21}+2k_{22}+2k_{23}+k_{24}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-50619cdd1627a2e7532a9d40ab710ac8_l3.png)
where:
![Rendered by QuickLaTeX.com \[\begin{split} k_{11}&=F_1(x_i,y_i,t_i)=y_i\\ k_{21}&=F_2(x_i,y_i,t_i)=10-x_i-0.15y_i\\ k_{12}&=F_1\left(x_i+\frac{h}{2}k_{11},y_i+\frac{h}{2}k_{21},t_i+\frac{h}{2}\right)=y_i+\frac{h}{2}k_{21}\\ k_{22}&=F_2\left(x_i+\frac{h}{2}k_{11},y_i+\frac{h}{2}k_{21},t_i+\frac{h}{2}\right)=10-(x_i+\frac{h}{2}k_{11})-0.15(y_i+\frac{h}{2}k_{21})\\ k_{13}&=F_1\left(x_i+\frac{h}{2}k_{12},y_i+\frac{h}{2}k_{22},t_i+\frac{h}{2}\right)=y_i+\frac{h}{2}k_{22}\\ k_{23}&=F_2\left(x_i+\frac{h}{2}k_{12},y_i+\frac{h}{2}k_{22},t_i+\frac{h}{2}\right)=10-(x_i+\frac{h}{2}k_{12})-0.15(y_i+\frac{h}{2}k_{22})\\ k_{14}&=F_1(x_i+hk_{13},y_i+hk_{23},t_i+h)=y_i+hk_{23}\\ k_{24}&=F_2(x_i+hk_{13},y_i+hk_{23},t_i+h)=10-(x_i+hk_{13})-0.15(y_i+hk_{23}) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d1c46b94d9390c992b712c22a571de35_l3.png)
With the initial conditions ![]() , the values of
, the values of ![]() can be calculated as:
can be calculated as:
![Rendered by QuickLaTeX.com \[\begin{split} k_{11}&=y_0=0\\ k_{21}&=10-x_0-0.15y_0=10\\ k_{12}&=y_0+\frac{h}{2}k_{21}=0+0.05\times 10=0.5\\ k_{22}&=10-(x_0+\frac{h}{2}k_{11})-0.15(y_0+\frac{h}{2}k_{21})\\ &=10-(0+0.05\times 0)-0.15(0+0.05\times 10)=9.925\\ k_{13}&=y_0+\frac{h}{2}k_{22}=0+0.05(9.925)=0.49625\\ k_{23}&=10-(x_0+\frac{h}{2}k_{12})-0.15(y_0+\frac{h}{2}k_{22})\\ &=10-(0+0.05\times 0.5)-0.15(0+0.05\times 9.925)=9.90056\\ k_{14}&=y_0+hk_{23}=0.1\times 9.90056=0.990056\\ k_{24}&=10-(x_0+hk_{13})-0.15(y_0+hk_{23})\\ &=10-(0+0.1\times 0.49625)-0.15(0+0.1\times 9.90056)=9.80187 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-419001ee06e3ee36eb8178c900b8d02b_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} x_1&=x_0+\frac{h}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\ &=0+\frac{0.1}{6}(0+2\times 0.5+2\times 0.49625+0.990056)=0.049709\\ y_1&=y_0+\frac{h}{6}(k_{21}+2k_{22}+2k_{23}+k_{24})\\ &=0+\frac{0.1}{6}(10+2\times 9.925+2\times 9.90056+9.80187)=0.990883 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2f6ffa642f7978d4f622e4082abd97d8_l3.png)
For ![]() and
and ![]() , the values of
, the values of ![]() can be calculated as:
can be calculated as:
![Rendered by QuickLaTeX.com \[\begin{split} k_{11}&=y_1=0.990883\\ k_{21}&=10-x_1-0.15y_1=10-0.049709-0.15\times 0.990883=9.80166\\ k_{12}&=y_1+\frac{h}{2}k_{21}=0.990883+0.05\times 9.80166=1.480966\\ k_{22}&=10-(x_1+\frac{h}{2}k_{11})-0.15(y_1+\frac{h}{2}k_{21})\\ &=10-(0.049709+0.05\times 0.990883)-0.15(0.990883+0.05\times 9.80166)=9.678902\\ k_{13}&=y_1+\frac{h}{2}k_{22}=0.990883+0.05(9.678902)=1.47482\\ k_{23}&=10-(x_1+\frac{h}{2}k_{12})-0.15(y_1+\frac{h}{2}k_{22})\\ &=10-(0.049709+0.05\times 1.480966)-0.15(0.990883+0.05\times 9.678902)=9.65502\\ k_{14}&=y_1+hk_{23}=0.990883+0.1\times 9.65502=1.956385\\ k_{24}&=10-(x_1+hk_{13})-0.15(y_1+hk_{23})\\ &=10-(0.049709+0.1\times 1.47482)-0.15(0.990883+0.1\times 9.65502)=9.50935 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-107d80cc07b94ad6c6e56fb0806254b8_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} x_2&=x_1+\frac{h}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\ &=0.049709+\frac{0.1}{6}(0.990883+2\times 1.480966+2\times 1.47482+1.956385)=0.197356\\ y_2&=y_1+\frac{h}{6}(k_{21}+2k_{22}+2k_{23}+k_{24})\\ &=0.990883+\frac{0.1}{6}(9.80166+2\times 9.678902+2\times 9.65502 +9.50935)=1.95719 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e8a307c14a4fee3a7791e84830baf428_l3.png)
Proceeding iteratively, the values of ![]() and
and ![]() up to
up to ![]() can be obtained. The Microsoft Excel file RK4System.xlsx shows the calculated up to the required time point.
can be obtained. The Microsoft Excel file RK4System.xlsx shows the calculated up to the required time point.
Comparison
The following figure shows the exact solution (blue curve) and the numerical solution (black dots) for the position ![]() and the velocity
and the velocity ![]() obtained using the explicit Euler method and the classical Runge-Kutta method. Using the explicit Euler method, the numerical solution deviates from the exact solution for higher values of
obtained using the explicit Euler method and the classical Runge-Kutta method. Using the explicit Euler method, the numerical solution deviates from the exact solution for higher values of ![]() . However, the classical Runge-Kutta method provides very accurate predictions. The Mathematica code utilized to produce the curves is shown below.
. However, the classical Runge-Kutta method provides very accurate predictions. The Mathematica code utilized to produce the curves is shown below.
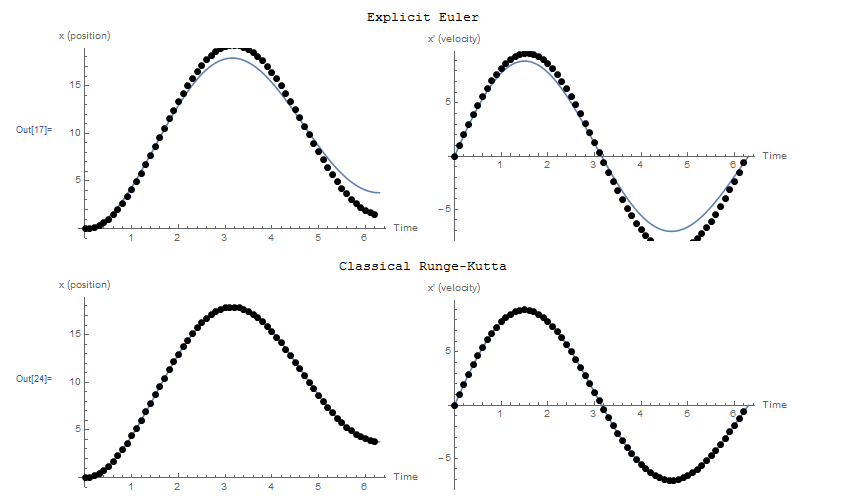
Clear[x]
a = DSolve[{x''[t] == 10 - x[t] - 0.15 x'[t], x'[0] == 0, x[0] == 0}, x, t]
x = x[t] /. a[[1]]
xp = Simplify[D[x, t]]
Plot[x, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, AxesLabel -> {"time", "x (position)"}]
Plot[xp, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, AxesLabel -> {"time", "x' (velocity)"}]
EulerMethod2[fp1_, fp2_, x10_, x20_, h_, t0_, tmax_] := (
n = (tmax - t0)/h + 1;
x1table = Table[0, {i, 1, n}];
x2table = Table[0, {i, 1, n}];
x1table[[1]] = x10;
x2table[[1]] = x20;
Do[x1table[[i]] = x1table[[i - 1]] + h*fp1[x1table[[i - 1]], x2table[[i - 1]], t0 + (i - 2) h];
x2table[[i]] = x2table[[i - 1]] + h*fp2[x1table[[i - 1]], x2table[[i - 1]], t0 + (i - 2) h],
{i, 2, n}];
Data = Table[{t0 + (i - 1)*h, x1table[[i]], x2table[[i]]}, {i, 1, n}];
Data)
RK4Method2[fp1_, fp2_, x10_, x20_, h_, t0_, tmax_] := (
n = (tmax - t0)/h + 1;
x1table = Table[0, {i, 1, n}];
x1table[[1]] = x10;
x2table = Table[0, {i, 1, n}];
x2table[[1]] = x20;
Do[k11 = fp1[x1table[[i - 1]], x2table[[i - 1]], t0 + (i - 2) h];
k21 = fp2[x1table[[i - 1]], x2table[[i - 1]], t0 + (i - 2) h];
k12 = fp1[x1table[[i - 1]] + h/2*k11, x2table[[i - 1]] + h/2*k21, t0 + (i - 1.5) h];
k22 = fp2[x1table[[i - 1]] + h/2*k11, x2table[[i - 1]] + h/2*k21, t0 + (i - 1.5) h];
k13 = fp1[x1table[[i - 1]] + h/2*k12, x2table[[i - 1]] + h/2*k22, t0 + (i - 1.5) h];
k23 = fp2[x1table[[i - 1]] + h/2*k12, x2table[[i - 1]] + h/2*k22, t0 + (i - 1.5) h];
k14 = fp1[x1table[[i - 1]] + h*k13, x2table[[i - 1]] + h*k23, t0 + (i - 1) h];
k24 = fp2[x1table[[i - 1]] + h*k13, x2table[[i - 1]] + h*k23, t0 + (i - 1) h];
x1table[[i]] = x1table[[i - 1]] + h (k11 + 2 k12 + 2 k13 + k14)/6;
x2table[[i]] = x2table[[i - 1]] + h (k21 + 2 k22 + 2 k23 + k24)/6, {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, x1table[[i]], x2table[[i]]}, {i, 1, n}];
Data2)
fp1[x_, y_, t_] := y;
fp2[x_, y_, t_] := 10 - x - 0.15 y;
Data = EulerMethod2[fp1, fp2, 0, 0, 0.1, 0, 2 Pi];
DataPosition = Drop[Data, None, {3}];
DataVelocity = Drop[Data, None, {2}];
a1 = Plot[x, {t, 0, 6.3}, Epilog -> {PointSize[Large], Point[DataPosition]}, AxesOrigin -> {0, 0}, ImageSize -> Medium, AxesLabel -> {"Time", "x (position)"}];
a2 = Plot[xp, {t, 0, 6.3}, Epilog -> {PointSize[Large], Point[DataVelocity]}, AxesOrigin -> {0, 0}, ImageSize -> Medium, AxesLabel -> {"Time", "x' (velocity)"}];
a = Grid[{{a1, a2}}];
Grid[{{"Explicit Euler"}, {a}}]
Data = RK4Method2[fp1, fp2, 0, 0, 0.1, 0, 2 Pi];
DataPosition = Drop[Data, None, {3}];
DataVelocity = Drop[Data, None, {2}];
a1 = Plot[x, {t, 0, 6.3}, Epilog -> {PointSize[Large], Point[DataPosition]}, ImageSize -> Medium, AxesOrigin -> {0, 0}, AxesLabel -> {"Time", "x (position)"}];
a2 = Plot[xp, {t, 0, 6.3}, Epilog -> {PointSize[Large], Point[DataVelocity]}, ImageSize -> Medium, AxesOrigin -> {0, 0}, AxesLabel -> {"Time", "x' (velocity)"}];
a = Grid[{{a1, a2}}];
Grid[{{"Classical Runge-Kutta"}, {a}}]
The effect of changing the value of ![]() on the resulting numerical solution for the system of IVPs given here can be illustrated using the following tool. Even for
on the resulting numerical solution for the system of IVPs given here can be illustrated using the following tool. Even for ![]() the classical Runge-Kutta produces very accurate predictions at which point the explicit Euler method produces very erroneous results.
the classical Runge-Kutta produces very accurate predictions at which point the explicit Euler method produces very erroneous results.
Using Mathematica
The built-in NDSolve in Mathematica uses the Runge-Kutta methods to solve a system of IVPs and produces piecewise interpolating polynomials for the dependent variables. The following code solves some of the preceding examples and compares with the exact solution. Note that in those examples when the exact and numerical solutions are plotted together, they overlap!
View Mathematica CodeClear[x, xn, xtable]
(*Example 1*)
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
b = NDSolve[{xn'[t] == k*xn[t], xn[0] == 35}, xn, {t, 0, 50}]
xn = xn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 50}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"t", "Population"}]
(*Example 2*)
Clear[cn]
b = NDSolve[{cn'[t] == (100 + 50*Cos[2 Pi*t/365])/10000*(5 Exp[-2 t/1000] - cn[t]), cn[0] == 5}, cn, {t, 0, 700}]
cn = cn /. b[[1]]
Plot[cn[t], {t, 0, 700}, AxesLabel -> {"t", "Concentration"}]
(*Example 4*)
Clear[xn, x]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
b = NDSolve[{xn'[t] == t*xn[t]^2 + 2 xn[t], xn[0] == -5}, xn, {t, 0, 5}]
xn = xn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 5}, PlotRange -> All, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"t", "x"}]
(*Example of a system*)
Clear[xn, yn, x]
a = DSolve[{x''[t] == 10 - x[t] - 0.15 x'[t], x'[0] == 0, x[0] == 0}, x, t]
x = x[t] /. a[[1]]
xp = Simplify[D[x, t]]
b = NDSolve[{xn'[t] == yn[t], yn'[t] == 10 - xn[t] - 0.15 yn[t], xn[0] == 0, yn[0] == 0}, {xn, yn}, {t, 0, 2 Pi}]
xn = xn /. b[[1]]
yn = yn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"time", "x (position)"}]
Plot[{xp, yn[t]}, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"time", "x' (velocity)"}]
Solution Methods for BVPs
As mentioned above, BVP are ordinary differential equations whose boundary conditions are given at different values of the independent variable. Usually, these points are the extreme points of the region of interest, or the “boundaries” of the domain and hence the term: “boundary value problem”. Consider a BVP with ![]() as the dependent variable and
as the dependent variable and ![]() as the independent variable. The boundary conditions would be given in terms of
as the independent variable. The boundary conditions would be given in terms of ![]() or the derivatives of
or the derivatives of ![]() at different values of the independent variable
at different values of the independent variable ![]() . When the boundary conditions are given in terms of
. When the boundary conditions are given in terms of ![]() , then, this type of boundary conditions is termed Dirichlet boundary condition. Otherwise, when the boundary conditions are given in terms of the derivatives of
, then, this type of boundary conditions is termed Dirichlet boundary condition. Otherwise, when the boundary conditions are given in terms of the derivatives of ![]() , this type of boundary conditions is termed Neumann boundary condition. A BVP is usually an ODE that is at least of the second-order as equations of the first order require only one boundary condition which is usually an initial boundary condition. There are various methods to solve boundary value problems; among them are the following:
, this type of boundary conditions is termed Neumann boundary condition. A BVP is usually an ODE that is at least of the second-order as equations of the first order require only one boundary condition which is usually an initial boundary condition. There are various methods to solve boundary value problems; among them are the following:
- Shooting method. In the shooting method the boundary value problem is solved as an initial value problem and the initial conditions are varied until the boundary conditions at the extreme ends are satisfied. For example, consider the BVP
![Rendered by QuickLaTeX.com \[ \frac{\mathrm{d}^2y}{\mathrm{d}x^2}=f(x) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-adc29dce7299fe4545274d9e3c1c0b68_l3.png)
with the boundary conditions:
![Rendered by QuickLaTeX.com \[ y(0)=y_0\qquad y(L)=y_L \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d7222b0400a61c385f7df3019aabc478_l3.png)
Then, the system can be converted into an initial value problem with the following boundary conditions:
![Rendered by QuickLaTeX.com \[ y(0)=y_0\qquad y'(0)=s \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-51de8f7de3bd2c4a28df346b7d0ba1cd_l3.png)
After a solution is obtained, the value of
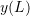 is compared to
is compared to 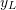 and
and  is varied and the solution is repeated until
is varied and the solution is repeated until 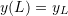 .
. - Finite difference method. The finite difference method relies on approximating the BVP with difference equations by replacing the derivatives of the function with their finite difference approximations.
- Weak formulation methods. The weak formulation methods rely on converting the problem into a different “integral” form and finding the best solution that would satisfy the new form. Examples of such methods are the finite element analysis method or the weighted residuals methods.
The finite difference method is the only method that we will cover in these notes.
Finite Difference Method
Consider a BVP with the dependent variable ![]() and the independent variable
and the independent variable ![]() with
with ![]() . The finite difference method in a BVP relies on discretizing the domain
. The finite difference method in a BVP relies on discretizing the domain ![]() into
into ![]() intervals with
intervals with ![]() with a constant step size
with a constant step size ![]() . The values of the dependent variable at the interval junctions are denoted by:
. The values of the dependent variable at the interval junctions are denoted by: ![]() . The finite difference method seeks to find a numerical solution to each
. The finite difference method seeks to find a numerical solution to each ![]() by solving difference equations formed by replacing the derivatives in the BVP with a finite difference approximation scheme (usually the centred finite difference scheme). Dirichlet boundary conditions can be directly imposed on the known values of
by solving difference equations formed by replacing the derivatives in the BVP with a finite difference approximation scheme (usually the centred finite difference scheme). Dirichlet boundary conditions can be directly imposed on the known values of ![]() while Neumann boundary conditions can be imposed as additional difference equations using an appropriate finite difference scheme. The following examples show how the method can be implemented.
while Neumann boundary conditions can be imposed as additional difference equations using an appropriate finite difference scheme. The following examples show how the method can be implemented.
Example 1
In this example, we first derive the heat equation and then attempt to solve it using the finite difference method.
Heat Equation Derivation: The differential equation describing thermal energy within objects (Steady State Heat Equation) is one example of a BVP that can be solved using the finite difference method. In this example, the steady state heat equation is first derived for a one-dimensional rod of length 10m connecting two heat sources of constant temperature as shown in the figure such that the temperature of the rod at the end ![]() is equal to
is equal to ![]() C while the temperature at the other end
C while the temperature at the other end ![]() is equal to
is equal to ![]() C. The ambient temperature around the rod is equal to
C. The ambient temperature around the rod is equal to ![]() C. The steady state heat equation can be derived by balancing the amount of heat energy per unit time entering and exiting through a control length of the rod. The amount of heat energy transferred to the ambient environment per unit time and per unit length is equal to
C. The steady state heat equation can be derived by balancing the amount of heat energy per unit time entering and exiting through a control length of the rod. The amount of heat energy transferred to the ambient environment per unit time and per unit length is equal to
![]()
With ![]() units for this example. The amount of heat energy transferred through the rod per unit time is equal to:
units for this example. The amount of heat energy transferred through the rod per unit time is equal to:
![]()
With ![]() units in this example. The negative sign is essential as heat energy is transferred from areas of high temperature to areas of lower temperature. The steady state differential equation can be derived by equating the amount of energy entering to the amount of energy exiting per unit time considering a control length equal to
units in this example. The negative sign is essential as heat energy is transferred from areas of high temperature to areas of lower temperature. The steady state differential equation can be derived by equating the amount of energy entering to the amount of energy exiting per unit time considering a control length equal to ![]() as shown in the figure below:
as shown in the figure below:
![]()
Where a Taylor series with only two terms was used to approximate ![]() . Therefore:
. Therefore:
![]()
The solution to this equation provides the temperature distribution (with ![]() being the dependent variable) within the rod (with
being the dependent variable) within the rod (with ![]() as the independent variable).
as the independent variable).
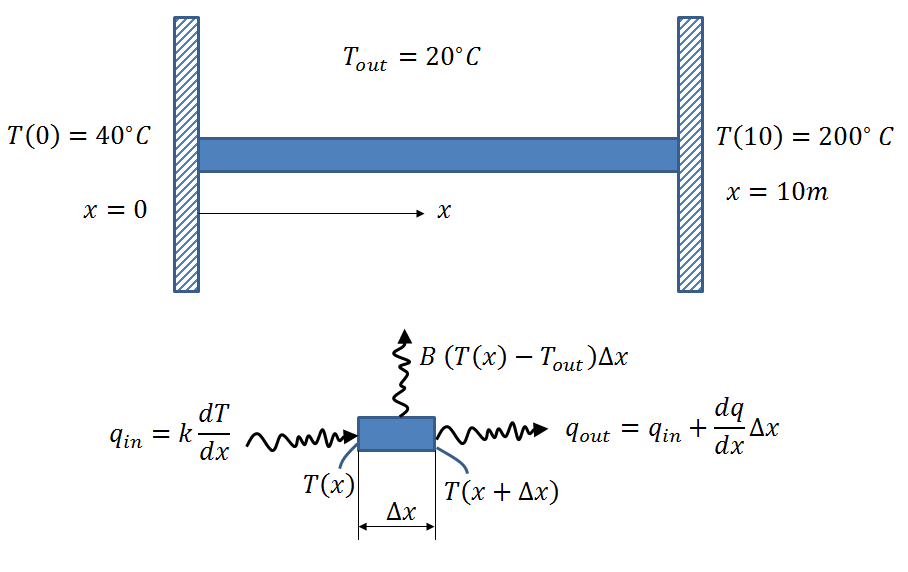
Statement of Problem: Consider the BVP developed above with the Dirichlet boundary conditions ![]() and
and ![]() .
.
- Find the exact solution of the differential equation.
- Use the finite difference method with
 intervals to find a numerical solution to the BVP.
intervals to find a numerical solution to the BVP.
Repeat the problem considering the two boundary conditions: the Dirichlet boundary condition ![]() and the Neumann boundary condition
and the Neumann boundary condition
![]()
Solution
Dirichlet Boundary Conditions
The exact solution can be directly obtained in Mathematica using the DSolve function. Note that an exact solution is not always available.
![]()
The numerical solution is obtained by first discretizing the domain into ![]() intervals with
intervals with ![]() and
and ![]() . The values of
. The values of ![]() at these points are denoted by
at these points are denoted by ![]() . The boundary conditions are given as Dirichlet type with
. The boundary conditions are given as Dirichlet type with ![]() and
and ![]() . The remaining 3 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 equations of the form:
. The remaining 3 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 equations of the form:
![]()
This results in the following three equations (after the substitution ![]() and
and ![]() ):
):
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{T_2-2T_1+40}{6.25} &=\frac{1}{10}\left(T_1-20\right)\\ \frac{T_3-2T_2+T_1}{6.25} &=\frac{1}{10}\left(T_2-20\right)\\ \frac{200-2T_3+T_2}{6.25} &=\frac{1}{10}\left(T_3-20\right) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9a07fc9c08ea9b95b42cc1091cf026b2_l3.png)
Rearranging yields the following linear system of equations:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}-0.42&0.16&0\\0.16&-0.42&0.16\\0&0.16&-0.42 \end{matrix}\right)\left(\begin{array}{c}T_1\\T_2\\T_3\end{array}\right)=\left(\begin{array}{c}-8.4\\-2\\-34\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-22deb663a218cc598fa332eaee85afff_l3.png)
Solving the above system yields:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{c}T_1\\T_2\\T_3\end{array}\right)=\left(\begin{array}{c}43.1979\\60.8946\\104.15\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c92d08acc909de60797b5e7ac9cafc74_l3.png)
Combined with ![]() and
and ![]() , a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The figure shows that the numerical solution is almost identical to the exact solution.
, a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The figure shows that the numerical solution is almost identical to the exact solution.
View Mathematica Code
ClearAll["Global`*"]
hp = 1/10;
n = 4;
L = 10 - 0;
h = L/n;
Ts = Table[Symbol["T" <> ToString[i]], {i, 0, n}]
T0 = 40;
Ts[[n + 1]] = 200;
Ts // MatrixForm
Equations = Table[(Ts[[i + 1]] - 2 Ts[[i]] + Ts[[i - 1]])/h^2 == hp*(Ts[[i]] - 20), {i, 2, n}];
Equations // MatrixForm
Equations = Expand[Equations];
Equations // MatrixForm
N[Equations] // MatrixForm
unknowns = Table[Symbol["T" <> ToString[i]], {i, 1, n - 1}]
a = Solve[Equations, unknowns]
Ts = Ts /. a[[1]]
SolList = Table[{0 + (i)*h, Ts[[i + 1]]}, {i, 0, n}];
SolList // MatrixForm
a = DSolve[{T''[x] == hp*(T[x] - 20), T[0] == 40, T[10] == 200}, T, x]
T = T[x] /. a[[1]];
FullSimplify[N[T]]
Plot[T, {x, 0, 10}, AxesLabel -> {"distance x (m)", "Temperature T (Celsius)"}, AxesOrigin -> {0, 0}, Epilog -> {PointSize[Large], Point[SolList]}]
In the following tool, vary the number of intervals ![]() to show the effect on the numerical solution:
to show the effect on the numerical solution:
Dirichlet and Neumann Boundary Conditions
The exact solution can be directly obtained in Mathematica using the DSolve function. Note that an exact solution is not always available.
![]()
The numerical solution is obtained by first discretizing the domain into ![]() intervals with
intervals with ![]() and
and ![]() . The values of
. The values of ![]() at these points are denoted by
at these points are denoted by ![]() . The Dirichlet boundary condition can be used to set
. The Dirichlet boundary condition can be used to set ![]() . The remaining 4 unknowns can be obtained using four equations. Three equations are composed by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation at the three intermediate points. The fourth equation is composed by utilizing the backward finite difference scheme at
. The remaining 4 unknowns can be obtained using four equations. Three equations are composed by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation at the three intermediate points. The fourth equation is composed by utilizing the backward finite difference scheme at ![]() and equate it to the Neumann boundary condition. The three difference equations at the intermediate points have the form:
and equate it to the Neumann boundary condition. The three difference equations at the intermediate points have the form:
![]()
This results in the following three equations (after the substitution ![]() ):
):
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{T_2-2T_1+40}{6.25} &=\frac{1}{10}\left(T_1-20\right)\\ \frac{T_3-2T_2+T_1}{6.25} &=\frac{1}{10}\left(T_2-20\right)\\ \frac{T_4-2T_3+T_2}{6.25} &=\frac{1}{10}\left(T_3-20\right) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-da5e0328a87baf7348dbf140b9551993_l3.png)
The fourth equation can be obtained using the backward finite difference at point ![]() :
:
![]()
Combining the four equations and rearranging yields the following linear system of equations:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}-0.42&0.16&0&0\\0.16&-0.42&0.16&0\\0&0.16&-0.42&0.16\\0&0&-0.4&0.4 \end{matrix}\right)\left(\begin{array}{c}T_1\\T_2\\T_3\\T_4\end{array}\right)=\left(\begin{array}{c}-8.4\\-2\\-2\\-3\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-605267fac60cb2ecbb1b71c3b50d4bb0_l3.png)
Solving the above system yields:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{c}T_1\\T_2\\T_3\\T_4\end{array}\right)=\left(\begin{array}{c}28.3216\\21.8443\\16.5195\\9.01954\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b55fb1b84438c74870c6283616456c7a_l3.png)
Combined with ![]() , a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The figure shows that the numerical solution of the same differential equation with Neumann boundary conditions provides less accurate results than the solution when Dirichlet boundary conditions were used.
, a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The figure shows that the numerical solution of the same differential equation with Neumann boundary conditions provides less accurate results than the solution when Dirichlet boundary conditions were used.
View Mathematica Code
ClearAll["Global`*"]
hp = 1/10;
n = 4;
L = 10 - 0;
h = L/n;
Ts = Table[Symbol["T" <> ToString[i]], {i, 0, n}]
T0 = 40;
Ts // MatrixForm
Equations = Table[(Ts[[i + 1]] - 2 Ts[[i]] + Ts[[i - 1]])/h^2 == hp*(Ts[[i]] - 20), {i, 2, n}];
NeumannEquation = ((Ts[[n + 1]] - Ts[[n]])/h == -3);
Equations = Append[Equations, NeumannEquation];
Equations // MatrixForm
Equations = Expand[Equations];
Equations // MatrixForm
N[Equations] // MatrixForm
unknowns = Table[Symbol["T" <> ToString[i]], {i, 1, n}]
a = Solve[Equations, unknowns];
Ts = N[Ts /. a[[1]]]
SolList = Table[{0 + (i)*h, Ts[[i + 1]]}, {i, 0, n}];
SolList // MatrixForm
a = DSolve[{T''[x] == hp*(T[x] - 20), T[0] == 40, T'[10] == -3}, T, x]
T = T[x] /. a[[1]];
FullSimplify[N[T]]
Plot[T, {x, 0, 10}, AxesLabel -> {"distance x (m)", "Temperature T (Celsius)"}, AxesOrigin -> {0, 0}, Epilog -> {PointSize[Large], Point[SolList]}]
The numerical solution approaches the exact solution as the number of intervals is increased. Vary ![]() in the following tool and observe how it affects the numerical solution.
in the following tool and observe how it affects the numerical solution.
Example 2
Consider the following second-order BVP:
![]()
with the boundary conditions:
![]()
Use the finite difference method to find a numerical solution to the above equation by dividing the domain ![]() into
into ![]() intervals. Compare with the exact solution.
intervals. Compare with the exact solution.
Solution
The exact solution can be directly obtained in Mathematica using the DSolve function. Note that an exact solution is not always available.
![]()
The numerical solution is obtained by first discretizing the domain into ![]() intervals with
intervals with ![]() and
and ![]() . The values of
. The values of ![]() at these points are denoted by
at these points are denoted by ![]() . The boundary conditions are given as Dirichlet type with
. The boundary conditions are given as Dirichlet type with ![]() and
and ![]() . The remaining 4 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 equations of the form:
. The remaining 4 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 equations of the form:
![]()
This results in the following four equations (after the substitution ![]() and
and ![]() ):
):
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{u_{2}-2u_1+1.5}{0.36}+\frac{u_{2}-1.5}{1.2}+u_1&=1\\ \frac{u_{3}-2u_2+u_1}{0.36}+\frac{u_{3}-u_1}{1.2}+u_2&=1\\ \frac{u_{4}-2u_3+u_2}{0.36}+\frac{u_{4}-u_2}{1.2}+u_3&=1\\ \frac{2.5-2u_4+u_3}{0.36}+\frac{2.5-u_3}{1.2}+u_4&=1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7eb07581ea72bca6db5574beafcb5c10_l3.png)
Rearranging yields the following linear system of equations:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}-4.556&3.611&0&0\\1.944&-4.556&3.611&0\\0&1.944&-4.556&3.611\\0&0&1.944&-4.556\end{matrix}\right)\left(\begin{array}{c}u_1\\u_2\\u_3\\u_4\end{array}\right)=\left(\begin{array}{c}-1.91667\\1\\1\\-8.02778\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d651d65d10acbddca4121520605c7b1b_l3.png)
Solving the above system yields:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{c}u_1\\u_2\\u_3\\u_4\end{array}\right)=\left(\begin{array}{c}7.649\\9.1183\\7.6615\\5.0323\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8954d32116595554862d2fdc02a1e96b_l3.png)
Combined with ![]() and
and ![]() , a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The maximum error in the numerical solution is obtained at
, a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The maximum error in the numerical solution is obtained at ![]() . At this location, the exact solution is given by
. At this location, the exact solution is given by ![]() while the numerical solution is given by
while the numerical solution is given by ![]() with a relative error of -19%:
with a relative error of -19%:
![]()
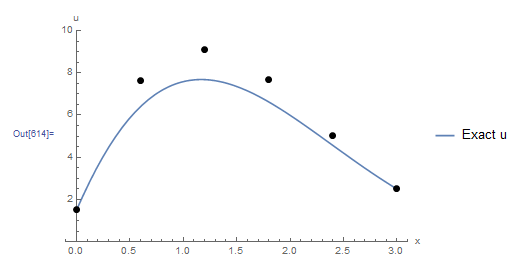
ClearAll["Global`*"]
n = 5;
L = 3 - 0;
h = L/n;
us = Table[Symbol["u" <> ToString[i]], {i, 0, n}]
u0 = 1.5;
us[[n + 1]] = 2.5;
us // MatrixForm
Equations = Table[(us[[i + 1]] - 2 us[[i]] + us[[i - 1]])/h^2 + (us[[i + 1]] - us[[i - 1]])/2/h + us[[i]] == 1, {i, 2, n}];
Equations // MatrixForm
Equations = Expand[Equations];
Equations // MatrixForm
N[Equations] // MatrixForm
unknowns = Table[Symbol["u" <> ToString[i]], {i, 1, n - 1}]
a = Solve[Equations, unknowns]
us = us /. a[[1]]
SolList = Table[{0 + (i)*h, us[[i + 1]]}, {i, 0, n}];
SolList // MatrixForm;
Clear[u]
(*Exact Solution*)
b = DSolve[{u''[x] + u'[x] + u[x] == 1, u[0] == 15/10, u[3] == 25/10}, u, x]
u = FullSimplify[u[x] /. b[[1]], Reals]
Plot[u, {x, 0, 3}, PlotLegends -> {"Exact u"}, AxesLabel -> {"x", "u"}, Epilog -> {PointSize[Large], Point[SolList]}, PlotRange -> {{-0.1, 3.1}, {0, 10}}]
Print["u at x=1.2 is ", uexact = u /. x -> 1.2]
Print["u_2 is ", u2 = u2 /. a[[1]]]
Print["Relative Error is ", (uexact - u2)/uexact]
In a BVP, the accuracy of the solution depends on the accuracy of the finite difference scheme used. As shown in the following tool, by decreasing the value of ![]() , the numerical solution gets closer to the exact solution.
, the numerical solution gets closer to the exact solution.
Example 3
The differential equation describing the displacement of a hanging chain as a function of the weight per unit length ![]() of the chain and the desired horizontal tension in the chain
of the chain and the desired horizontal tension in the chain ![]() is given by:
is given by:
![]()
Where ![]() is the dependent variable being the chain curve and
is the dependent variable being the chain curve and ![]() is the independent variable being the horizontal distance. The solution to this equation, namely the function
is the independent variable being the horizontal distance. The solution to this equation, namely the function ![]() is called the catenary or the curve that describes the hanging chain. See this page for a detailed derivation and some of the properties of the curve.
is called the catenary or the curve that describes the hanging chain. See this page for a detailed derivation and some of the properties of the curve.
If the boundary conditions are given by ![]() and
and ![]() and if
and if ![]() and
and ![]() units, then use the finite difference method to find a numerical solution by dividing the domain
units, then use the finite difference method to find a numerical solution by dividing the domain ![]() into
into ![]() intervals. Compare with the exact solution.
intervals. Compare with the exact solution.
Solution
Notice that this equation is a nonlinear second-order differential equation. Its exact solution describing the catenary of the chain can be obtained using the built-in Integrate function in Mathematica and has the form:
![]()
The numerical solution is obtained by first discretizing the domain into ![]() intervals with
intervals with ![]() and
and ![]() . The values of
. The values of ![]() at these points are denoted by
at these points are denoted by ![]() . The boundary conditions are given as Dirichlet type with
. The boundary conditions are given as Dirichlet type with ![]() and
and ![]() . The remaining 4 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 nonlinear equations of the form:
. The remaining 4 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 4 nonlinear equations of the form:
![]()
This results in the following four nonlinear equations (after the substitution ![]() and
and ![]() ):
):
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{y_2-2y_1+0}{0.64}&=\sqrt{1+\left(\frac{y_2-0}{1.6}\right)^2}\\ \frac{y_3-2y_2+y_1}{0.64}&=\sqrt{1+\left(\frac{y_3-y_1}{1.6}\right)^2}\\ \frac{y_4-2y_3+y_2}{0.64}&=\sqrt{1+\left(\frac{y_4-y_2}{1.6}\right)^2}\\ \frac{0-2y_4+y_3}{0.64}&=\sqrt{1+\left(\frac{0-y_3}{1.6}\right)^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a32e9aca334f9e658b00759f994d5db6_l3.png)
Notice that the resulting equations are nonlinear because the differential equation itself was nonlinear. The above system can be solved using the Newton-Raphson method with initial guesses of ![]() for all of the unknowns which yields the following solution:
for all of the unknowns which yields the following solution:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{c}y_1\\y_2\\y_3\\y_4\end{array}\right)=\left(\begin{array}{c}-1.92863\\-2.62693\\-2.62693\\-1.92863\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a3abc26268581027ccb5cef65ec285e5_l3.png)
Combined with ![]() and
and ![]() , a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The two solutions are very close to each other.
, a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The two solutions are very close to each other.
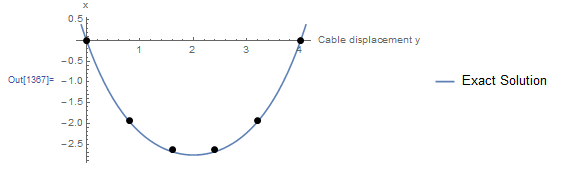
ClearAll["Global`*"]
w = 1.;
T = 1;
a = DSolve[{y''[x] == w/T*Sqrt[1 + (y'[x])^2], y[0] == 0, y[4] == 0},y, x]
y = FullSimplify[y[x] /. a[[1]]]
Plot[y, {x, 0, 4}]
L = 4 - 0
n = 5;
h = L/n;
ys = Table[Symbol["y" <> ToString[i]], {i, 0, n}];
y0 = 0;
ys[[n + 1]] = 0;
ys // MatrixForm
Equations = Table[(ys[[i + 1]] - 2 ys[[i]] + ys[[i - 1]])/h^2 == w/T*Sqrt[1 + ((ys[[i + 1]] - ys[[i - 1]])/2/h)^2], {i, 2, n}];
Equations // MatrixForm
unknowns = Table[Symbol["y" <> ToString[i]], {i, 1, n - 1}];
Initvalues = Table[{unknowns[[i]], -0.1}, {i, 1, n - 1}];
a = FindRoot[Equations, Initvalues]
ys = ys /. a
SolList = Table[{0 + (i)*h, ys[[i + 1]]}, {i, 0, n}];
Plot[y, {x, -0.1, 4.1}, AxesLabel -> {"Cable displacement y", "x"}, PlotLegends -> {"Exact Solution"}, Epilog -> {PointSize[Large], Point[SolList]}]
As shown in the following tool, by decreasing the value of ![]() , the numerical solution gets closer to the exact solution.
, the numerical solution gets closer to the exact solution.
Example 4
Consider the following BVP
![]()
With the boundary conditions ![]() and
and ![]() . Assuming
. Assuming ![]() , use the finite difference method to find a numerical solution to the given BVP. Compare with the exact solution.
, use the finite difference method to find a numerical solution to the given BVP. Compare with the exact solution.
Solution
The exact solution can be directly obtained in Mathematica using the DSolve function.
![]()
The numerical solution is obtained by first discretizing the domain into ![]() intervals with
intervals with ![]() and
and ![]() ,
, ![]() . The values of
. The values of ![]() at these points are denoted by
at these points are denoted by ![]() . The boundary conditions are given as Dirichlet type with
. The boundary conditions are given as Dirichlet type with ![]() and
and ![]() . The remaining 9 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 9 equations of the form:
. The remaining 9 unknowns can be obtained by utilizing the basic formulas of the centred finite difference scheme to replace the derivatives in the differential equation. These can be utilized to write 9 equations of the form:
![]()
This results in the following four equations (after the substitution ![]() and
and ![]() ):
):
![Rendered by QuickLaTeX.com \[ \begin{split} 7\left(\frac{y_2-2y_1+5}{4}\right)-\frac{y_2-5}{2}-y_1+x_1&=0\\ 7\left(\frac{y_3-2y_2+y_1}{4}\right)-\frac{y_3-y_1}{2}-y_2+x_2&=0\\ 7\left(\frac{y_4-2y_3+y_2}{4}\right)-\frac{y_4-y_2}{2}-y_3+x_3&=0\\ 7\left(\frac{y_5-2y_4+y_3}{4}\right)-\frac{y_5-y_3}{2}-y_4+x_4&=0\\ 7\left(\frac{y_6-2y_5+y_4}{4}\right)-\frac{y_6-y_4}{2}-y_5+x_5&=0\\ 7\left(\frac{y_7-2y_6+y_5}{4}\right)-\frac{y_7-y_5}{2}-y_6+x_6&=0\\ 7\left(\frac{y_8-2y_7+y_6}{4}\right)-\frac{y_8-y_6}{2}-y_7+x_7&=0\\ 7\left(\frac{y_9-2y_8+y_7}{4}\right)-\frac{y_9-y_7}{2}-y_8+x_8&=0\\ 7\left(\frac{8-2y_9+y_8}{4}\right)-\frac{8-y_8}{2}-y_9+x_9&=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7b80109cd7c8b2dacb7b9a7b3e248db4_l3.png)
Rearranging yields the following linear system of equations:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}-4.5&1.25&0&0&0&0&0&0&0\\2.25&-4.5&1.25&0&0&0&0&0&0\\0&2.25&-4.5&1.25&0&0&0&0&0\\0&0&2.25&-4.5&1.25&0&0&0&0\\0&0&0&2.25&-4.5&1.25&0&0&0\\0&0&0&0&2.25&-4.5&1.25&0&0\\0&0&0&0&0&2.25&-4.5&1.25&0\\0&0&0&0&0&0&2.25&-4.5&1.25\\0&0&0&0&0&0&0&2.25&-4.5\end{matrix}\right)\left(\begin{array}{c}y_1\\y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\\y_9\end{array}\right)=\left(\begin{array}{c}-13.25\\-4\\-6\\-8\\-10\\-12\\-14\\-16\\-28\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-db4d72060a28134e9dae85e755415aaf_l3.png)
Solving the above system yields:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{c}y_1\\y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\\y_9\end{array}\right)=\left(\begin{array}{c}4.19959\\4.51853\\5.50744\\6.89345\\8.50301\\10.2026\\11.824\\13.0018\\12.7231\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c10b708d5bf9e2bd48460c5da98ad72c_l3.png)
Combined with ![]() and
and ![]() , a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The numerical solution exactly overlaps the exact solution!
, a list plot can be drawn to show the obtained numerical solution. The following figure shows the exact solution (blue curve) with the numerical solution (black dots). The numerical solution exactly overlaps the exact solution!
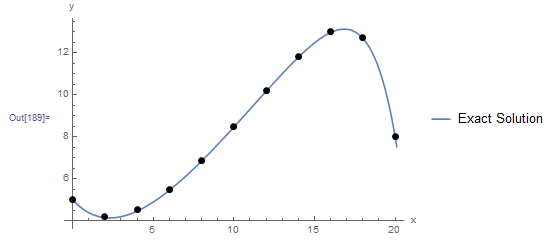
View Mathematica Code
ClearAll["Global`*"]
a = DSolve[{7 y''[x] - 2 y'[x] - y[x] + x == 0, y[0] == 5, y[20] == 8}, y, x]
y = FullSimplify[y[x] /. a[[1]]]
y = FullSimplify[N[y]]
Plot[y, {x, 0, 20}]
L = 20 - 0
n = 10;
h = L/n;
ys = Table[Symbol["y" <> ToString[i]], {i, 0, n}];
y0 = 5;
ys[[n + 1]] = 8;
ys // MatrixForm
Equations = Table[7 (ys[[i + 1]] - 2 ys[[i]] + ys[[i - 1]])/h^2 - 2 (ys[[i + 1]] - ys[[i - 1]])/2/h - ys[[i]] + 0 + (i - 1)*h == 0, {i, 2, n}];
Equations // MatrixForm
Expand[N[Equations]] // MatrixForm
unknowns = Table[Symbol["y" <> ToString[i]], {i, 1, n - 1}];
a = Solve[Equations, unknowns];
ys = N[ys /. a[[1]]]
SolList = Table[{0 + (i)*h, ys[[i + 1]]}, {i, 0, n}];
Plot[y, {x, -0.1, 20.1}, AxesLabel -> {"x", "y"}, PlotLegends -> {"Exact Solution"}, Epilog -> {PointSize[Large], Point[SolList]}]
Problems
- The current code given in the explicit Euler method assumes that
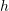 is chosen such that
is chosen such that 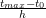 is a natural number. Modify the code so that if this is not the case, the solution for the dependent variable at
is a natural number. Modify the code so that if this is not the case, the solution for the dependent variable at  is available.
is available. - Consider the following IVP:
![Rendered by QuickLaTeX.com \[ \frac{\mathrm{d}x}{\mathrm{d}t}=xt+4x \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e0414d3e92fea60547610ba3f266f867_l3.png)
with the initial condition
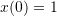 .
.- Use the built-in DSolve function to find the exact solution and plot
 for
for ![Rendered by QuickLaTeX.com t\in[0,1]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-01b4d55b618d2d00a8e00f96917d0951_l3.png) .
. - Use the explicit Euler method with
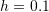 to find the values of
to find the values of 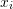 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution. - Use the implicit Euler method with
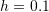 to find the values of
to find the values of 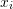 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution. - Use Heun’s method with
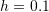 to find the values of
to find the values of 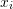 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution. - Use the midpoint method with
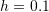 to find the values of
to find the values of 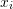 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution. - Use the classical Runge-Kutta method with
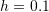 to find the values of
to find the values of 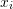 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution.
- Use the built-in DSolve function to find the exact solution and plot
- Consider a mass-spring system with
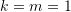 units,
units, 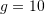 units with the initial conditions
units with the initial conditions 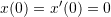 .
.
- Use the built-in DSolve function to find the exact solution and plot the position
 and velocity
and velocity 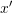 for
for ![Rendered by QuickLaTeX.com t\in[0,2\pi]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c6614feb82dce89a3a272a5ce39e00f9_l3.png) .
. - Use the explicit Euler method with
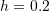 to find the values of
to find the values of 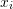 and
and 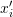 . Plot the exact solutions overlapping the obtained numerical solutions.
. Plot the exact solutions overlapping the obtained numerical solutions. - Use the classical Runge-Kutta method with
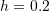 to find the values of
to find the values of  and
and 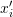 . Plot the exact solution overlapping the obtained numerical solution.
. Plot the exact solution overlapping the obtained numerical solution.
- Use the built-in DSolve function to find the exact solution and plot the position
- Consider the following IVP:
![Rendered by QuickLaTeX.com \[ y''(t)+9y=0 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9897f9c41889934dc9942c6cfa291e41_l3.png)
with the initial conditions
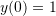 and
and 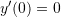 . Use the implicit Euler method to find a numerical solution to the given IVP for
. Use the implicit Euler method to find a numerical solution to the given IVP for ![Rendered by QuickLaTeX.com t\in[0,5]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-89b22c375e995ed042c407a9d648430b_l3.png) with
with 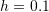 . Compare with the exact solution.
. Compare with the exact solution. - Consider the following IVP:
![Rendered by QuickLaTeX.com \[ y''(t)+2y'(t)+6y=\cos{(2t)} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ac5af68fe9f8affb627f9931510d9c7f_l3.png)
with the initial conditions
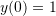 and
and 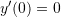 . Use the classical 4th-order Runge-Kutta method to find a numerical solution to the given IVP for
. Use the classical 4th-order Runge-Kutta method to find a numerical solution to the given IVP for ![Rendered by QuickLaTeX.com t\in[0,10]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ff10d62e92b48bda015872665c24c655_l3.png) with
with 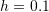 . Compare with the exact solution.
. Compare with the exact solution. - Consider the following nonlinear system of IVPs:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\mathrm{d}x}{\mathrm{d}t}&=10(y-x)\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=x(28-z)-y\\ \frac{\mathrm{d}z}{\mathrm{d}t}&=xy-\frac{8}{3}z\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-80289fd0c1c8a67532b6364da5675b24_l3.png)
with the initial conditions
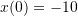 ,
, 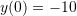 , and
, and 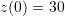 . Use the classical 4th-order Runge-Kutta method to find a numerical solution to the given IVP for
. Use the classical 4th-order Runge-Kutta method to find a numerical solution to the given IVP for ![Rendered by QuickLaTeX.com t\in[0,20]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0002f8f3f7178b78ba8675785a19eb04_l3.png) with
with 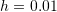 . Then, using list plots, plot the three curves showing
. Then, using list plots, plot the three curves showing 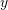 versus
versus  ,
,  versus
versus  , and
, and 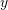 versus
versus  .
.
Note: The above system is an example of a Lorenz system of equations which can have chaotic solutions depending on the parameters used and the initial conditions. - Use the finite difference method to find a numerical solution to the following BVP:
![Rendered by QuickLaTeX.com \[ 4y''(x)-2y-x=0 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-091f68f5c316c4f2de705f9d11ceebc8_l3.png)
with the boundary conditions
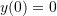 and
and 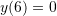 . Use
. Use 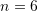 intervals, and compare with the exact solution.
intervals, and compare with the exact solution. -
The deflection
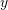 as a function of the position
as a function of the position  along the length of a simply supported Euler-Bernoulli beam uniformly loaded is given by:
along the length of a simply supported Euler-Bernoulli beam uniformly loaded is given by:
![Rendered by QuickLaTeX.com \[ EI\frac{\mathrm{d}^2y}{\mathrm{d}x^2}=\frac{wLx}{2}-\frac{wx^2}{2} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-17d001f13cf979a5267f176655738139_l3.png)
Where
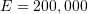 MPa is the Young’s modulus,
MPa is the Young’s modulus, 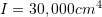 is the moment of inertia,
is the moment of inertia, 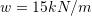 is the uniformly distributed load, and
is the uniformly distributed load, and 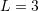 m is the length of the beam. The boundary conditions are given by
m is the length of the beam. The boundary conditions are given by 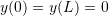 . Use the finite difference method to find a numerical solution to the deflection
. Use the finite difference method to find a numerical solution to the deflection 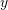 using
using 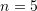 intervals. Compare with the exact solution.
intervals. Compare with the exact solution.