Engineering at Alberta Courses

A Brief Guide to Engineering Financial Calculations: Interest

Key Assumptions

For each method, the interest rate $\boldsymbol{i}$ is assumed to be for the interest period. For example, if the period is one year, then the interest rate $\boldsymbol{i}$ is the annual interest rate; but if the interest period is one month, then the interest rate for the period $\boldsymbol{i}$ would be 1/12 of the annual interest rate. Interest rate, discount rate, and return rate all mean the same thing.

Calculations

Direct calculation methods and interest tables were developed to solve a number of different simple cash flow series. These cash flows are idealized cases (which makes them good for midterm questions that test understanding); but in practice most cash flow series are complicated and are easier to solve using spreadsheets.

Single Payment Compound Amount: The future amount $\boldsymbol{F}$ at the end of $\boldsymbol{n}$ periods after depositing a sum $\boldsymbol{P}$ at the start of the $\boldsymbol{n}$ periods, with interest rate $\boldsymbol{i}$ .

In interest tables, use F = P x (F/P, i, n). The formula for direct calculation is:

$F = P * (1+i)^{n}$

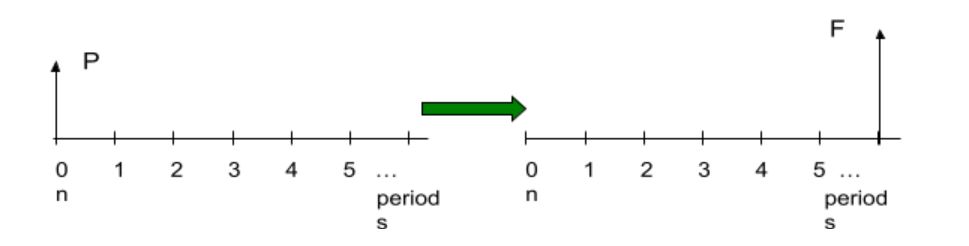
(This is the same as same as the compound interest calculation in the previous section for the future value of a present sum.)

Single Payment Present-Worth Amount: The present value $\boldsymbol{P}$ equivalent to a future amount $\boldsymbol{F}$ at the end of the $\boldsymbol{n}$ periods, with interest rate $\boldsymbol{i}$ .

In interest tables, use P = F x (P/F, i, n). The formula for direct calculation is:

$P = F * (1+i)^{-n}$

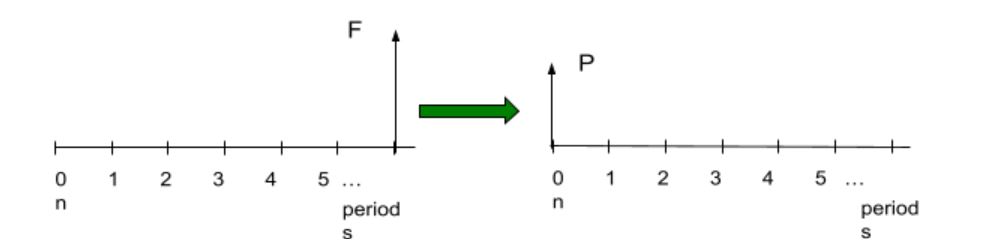
Uniform Series Compound Amount: The future amount $\boldsymbol{F}$ at the end of $\boldsymbol{n}$ periods after depositing a sum $\boldsymbol{A}$ at the end of each period with interest rate $\boldsymbol{i}$ .

In In interest tables, use F = A x (F/A, i, n). The formula for direct calculation is:

$F = A * (\frac{(1+i)^n-1}{i})$

Uniform Series Sinking Fund: The amount $\boldsymbol{A}$ that would have to be deposited at the end of the period for $\boldsymbol{n}$ periods with interest rate $\boldsymbol{i}$ to yield the future amount $\boldsymbol{F}$ .

In interest tables, use A = F x (A/F, i, n). The formula for direct calculation is:

$A = F * (\frac{i}{(1+i)^n-1})$

Uniform Series Capital Recovery: The size of payments $\boldsymbol{A}$ required at the end of each period to pay back a present sum $\boldsymbol{P}$ over $\boldsymbol{n}$ periods with interest rate $\boldsymbol{i}$ .

In interest tables, use A = P x (A/P, i, n). The formula for direct calculation is:

$A = P * (\frac{i*(1+i)^n}{(i+1)^n-1})$

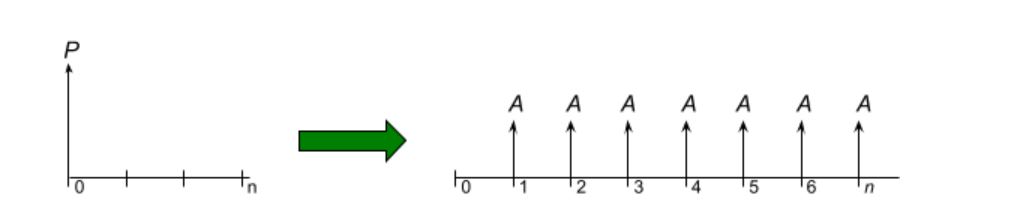
Capital Recovery Cost: A related calculation is the cost to recover capital, which is

CR = (P- S)(A|P, I, N) + iS

Uniform Series Present Worth: The present sum $\boldsymbol{P}$ that would be required to invest now to provide end-of-period payments of $\boldsymbol{A}$ for $\boldsymbol{n}$ periods with interest rate $\boldsymbol{i}$ .
In interest tables, use P = A x (P/A, i, n). The formula for direct calculation is:

$P = A * (\frac{(i+1)^n-1}{i*(1+i)^n})$

Arithmetic Gradient Present Worth: The present sum $\boldsymbol{P}$ from depositing a uniformly increasing series of sums, $\boldsymbol{G}$ , $\boldsymbol{2G}$ , etc., for $\boldsymbol{n-1}$ periods with interest rate $\boldsymbol{i}$ . Note that the sequence starts at zero payment at the end of the first period, and the $\boldsymbol{(n-1)^{th}}$ payment is at the end of period $\boldsymbol{n}$ .

In interest tables, use P = G x (P/G, i, n). The formula for direct calculation is:

$P = G * (\frac{(1+i)^n-i*n-1}{i^2*(1+i)^n})$

Arithmetic Gradient Future Worth: The future worth $\boldsymbol{F}$ at the end of n periods, from depositing a uniformly increasing series of sums, $\boldsymbol{G}$ at the end of the second period, $\boldsymbol{2G}$ at the end of the third period, etc., to $\boldsymbol{(n-1)G}$ at the end of period $\boldsymbol{n}$ , with interest rate $\boldsymbol{i}$ . Note that the sequence starts at zero payment at the end of the first period, and the $\boldsymbol{(n-1)^{th}}$ payment is at the end of period $\boldsymbol{n}$ .

In interest tables, use F = G x (F/G, i, n). The formula for direct calculation is:

$F = G * (\frac{(1+i)^n-i*n-1}{i^2})$

Geometric Series Present Worth: The present sum $\boldsymbol{P}$ from depositing an increasing series of sums, $\boldsymbol{A}$ at the end of period 1, $\boldsymbol{(1+g)A}$ at the end of period 2, etc., up to a deposit of $\boldsymbol{(1+g)^{n-1}*A}$ at the end of period $\boldsymbol{n}$ with interest rate $\boldsymbol{i}$ .

In interest tables, use P = A x (P/A, g, i, n). The formula for direct calculation is:

$if i \neq g$

$P = A * (\frac{1-(1+g)^n*(1+i)^{-n}}{i-g})$

otherwise:

$P = \frac{A*n}{1+i}$

Combinations

These formulæ can be used in combination to represent a more complicated set of cash flows, in a linear combination of series.

The formulæ can be used to convert from one type of series to another. One formula is used in an intermediate calculation of the equivalent $\boldsymbol{P}$ (or $\boldsymbol{F}$ , if you prefer), and then that value of $\boldsymbol{P}$ (or $\boldsymbol{F}$ ) is then substituted into another equation that yields the equivalent set of payments for a different type of series, or for an equivalent sum at a different point in time. Some examples include:

(F/P, i, N) = i(F/A, i, N) + 1(P/F, i, N) = 1 – (P/A, i, N)i

(A/F, i, N) = (A/P, i, N) – i

(A/P, i, N) = i / [1 – (P/F, i, N)]

(F/G, i, N) = (P/G, i, N)(F/P, i, N)(A/G, i, N) = (P/G, i, N)(A/P, i, N)

(F/A, g, i, N) = (P/A, g, i, N)(F/P, i, N)

Open Educational Resources

A Brief Guide to Engineering Financial Calculations: Interest

Leave a Reply Cancel reply