A Brief Guide to Engineering Financial Calculations: Analyzing New Investment
The Time-Value of Money & Equivalence
A sum of money is not worth as much in the future as it is today. Interest is the cost of having the use of some money until a time in the future, which could otherwise have been used for something else today. Money has to earn interest to maintain its value. Equivalence allows the value of money at one point in time to be expressed at another point in time, for a given interest rate.
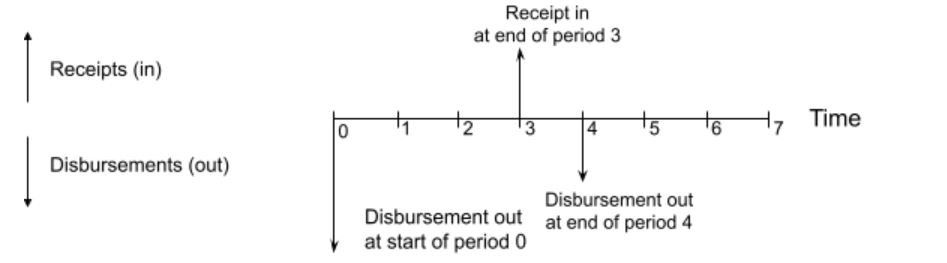
Cash Flow Diagram:
A cash flow diagram is used to visualize inflows and outflows over a time period. Time is plotted along a horizontal (divided into equal periods). Inflows are cash the company receives (also called receipts); these are shown as positive arrows which point up. Outflows are cash the company pays out (also called disbursements); these are shown as negative arrows which point down. The amount shown on the diagram is in terms of value at the time at which the activity takes place.
Key Assumptions
The original amount is called the Principal ![]() .
.
Simple interest calculates interest on the Principal only.
Compound interest calculates interest on the Principal as well as the previous interest.
Calculations
Simple Interest:
The future value of a present sum (the Principal) at an interest rate ![]() after
after ![]() interest periods is:
interest periods is:
![]()
Simple interest is almost never used in practice.
Compound Interest:
The future value of a present sum (the Principal) at an interest rate ![]() after
after ![]() interest periods is:
interest periods is:
![]()
This is consistent with our understanding that money has to earn interest to maintain its value into the future.
The present value of a sum ![]() periods in the future is calculated by using a negative value for the number of periods:
periods in the future is calculated by using a negative value for the number of periods:
![]()
Equivalent Annual Interest Rate:
While the interest rate is quoted for an annual basis, in reality most loans have payment periods that are different from one year. The Effective Annual Interest Rate (EAIR) is the annual interest rate that takes into account any compounding that occurs over the year:
where ![]() = the future sum,
= the future sum, ![]() = the present sum,
= the present sum, ![]() = nominal annual interest rate,
= nominal annual interest rate, ![]() = number of compounding periods per year, and
= number of compounding periods per year, and ![]() = number of years,
= number of years,
![]()
To find the future value of a present sum with some number of compounding periods per year, calculate it as though the interest rate was the EAIR compounded annually:
![]()
