A Brief Guide to Engineering Financial Calculations: Interest
Key Assumptions
For each method, the interest rate ![]() is assumed to be for the interest period. For example, if the period is one year, then the interest rate
is assumed to be for the interest period. For example, if the period is one year, then the interest rate ![]() is the annual interest rate; but if the interest period is one month, then the interest rate for the period
is the annual interest rate; but if the interest period is one month, then the interest rate for the period ![]() would be 1/12 of the annual interest rate. Interest rate, discount rate, and return rate all mean the same thing.
would be 1/12 of the annual interest rate. Interest rate, discount rate, and return rate all mean the same thing.
Calculations
Direct calculation methods and interest tables were developed to solve a number of different simple cash flow series. These cash flows are idealized cases (which makes them good for midterm questions that test understanding); but in practice most cash flow series are complicated and are easier to solve using spreadsheets.
Single Payment Compound Amount: The future amount ![]() at the end of
at the end of ![]() periods after depositing a sum
periods after depositing a sum ![]() at the start of the
at the start of the ![]() periods, with interest rate
periods, with interest rate ![]() .
.
In interest tables, use F = P x (F/P, i, n). The formula for direct calculation is:
![]()
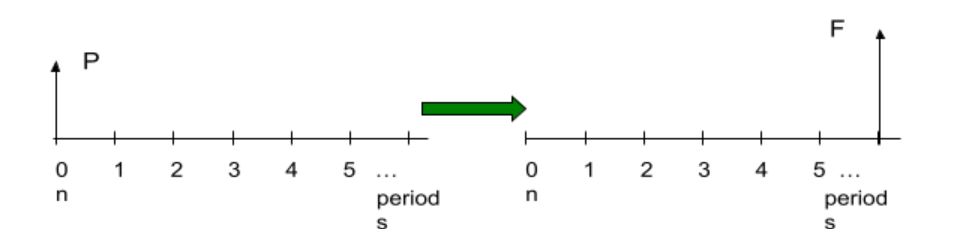
(This is the same as same as the compound interest calculation in the previous section for the future value of a present sum.)
Single Payment Present-Worth Amount: The present value ![]() equivalent to a future amount
equivalent to a future amount ![]() at the end of the
at the end of the ![]() periods, with interest rate
periods, with interest rate ![]() .
.
In interest tables, use P = F x (P/F, i, n). The formula for direct calculation is:
![]()
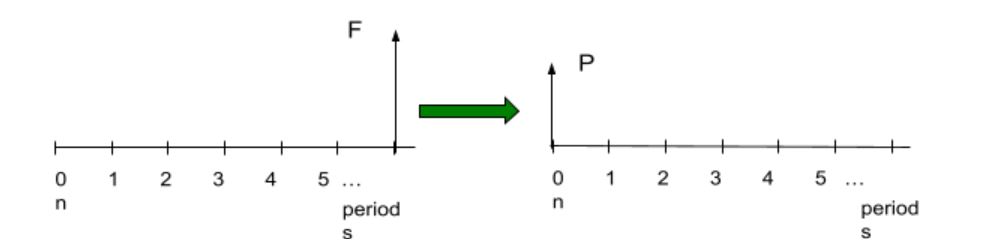
Uniform Series Compound Amount: The future amount ![]() at the end of
at the end of ![]() periods after depositing a sum
periods after depositing a sum ![]() at the end of each period with interest rate
at the end of each period with interest rate ![]() .
.
In In interest tables, use F = A x (F/A, i, n). The formula for direct calculation is:
![]()

Uniform Series Sinking Fund: The amount ![]() that would have to be deposited at the end of the period for
that would have to be deposited at the end of the period for ![]() periods with interest rate
periods with interest rate ![]() to yield the future amount
to yield the future amount ![]() .
.
In interest tables, use A = F x (A/F, i, n). The formula for direct calculation is:
![]()

Uniform Series Capital Recovery: The size of payments ![]() required at the end of each period to pay back a present sum
required at the end of each period to pay back a present sum ![]() over
over ![]() periods with interest rate
periods with interest rate ![]() .
.
In interest tables, use A = P x (A/P, i, n). The formula for direct calculation is:
![]()
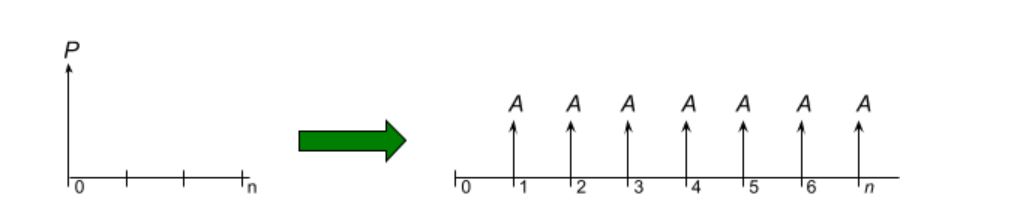
Capital Recovery Cost: A related calculation is the cost to recover capital, which is
CR = (P- S)(A|P, I, N) + iS
Uniform Series Present Worth: The present sum ![]() that would be required to invest now to provide end-of-period payments of
that would be required to invest now to provide end-of-period payments of ![]() for
for ![]() periods with interest rate
periods with interest rate ![]() .
.
In interest tables, use P = A x (P/A, i, n). The formula for direct calculation is:
![]()

Arithmetic Gradient Present Worth: The present sum ![]() from depositing a uniformly increasing series of sums,
from depositing a uniformly increasing series of sums, ![]() ,
, ![]() , etc., for
, etc., for ![]() periods with interest rate
periods with interest rate ![]() . Note that the sequence starts at zero payment at the end of the first period, and the
. Note that the sequence starts at zero payment at the end of the first period, and the ![]() payment is at the end of period
payment is at the end of period ![]() .
.
In interest tables, use P = G x (P/G, i, n). The formula for direct calculation is:
![]()

Arithmetic Gradient Future Worth: The future worth ![]() at the end of n periods, from depositing a uniformly increasing series of sums,
at the end of n periods, from depositing a uniformly increasing series of sums, ![]() at the end of the second period,
at the end of the second period, ![]() at the end of the third period, etc., to
at the end of the third period, etc., to ![]() at the end of period
at the end of period ![]() , with interest rate
, with interest rate ![]() . Note that the sequence starts at zero payment at the end of the first period, and the
. Note that the sequence starts at zero payment at the end of the first period, and the ![]() payment is at the end of period
payment is at the end of period ![]() .
.
In interest tables, use F = G x (F/G, i, n). The formula for direct calculation is:
![]()

Geometric Series Present Worth: The present sum ![]() from depositing an increasing series of sums,
from depositing an increasing series of sums, ![]() at the end of period 1,
at the end of period 1, ![]() at the end of period 2, etc., up to a deposit of
at the end of period 2, etc., up to a deposit of ![]() at the end of period
at the end of period ![]() with interest rate
with interest rate ![]() .
.
In interest tables, use P = A x (P/A, g, i, n). The formula for direct calculation is:
![]()
![]()
otherwise:
![]()

Combinations
These formulæ can be used in combination to represent a more complicated set of cash flows, in a linear combination of series.
The formulæ can be used to convert from one type of series to another. One formula is used in an intermediate calculation of the equivalent ![]() (or
(or ![]() , if you prefer), and then that value of
, if you prefer), and then that value of ![]() (or
(or ![]() ) is then substituted into another equation that yields the equivalent set of payments for a different type of series, or for an equivalent sum at a different point in time. Some examples include:
) is then substituted into another equation that yields the equivalent set of payments for a different type of series, or for an equivalent sum at a different point in time. Some examples include:
(F/P, i, N) = i(F/A, i, N) + 1(P/F, i, N) = 1 – (P/A, i, N)i
(A/F, i, N) = (A/P, i, N) – i
(A/P, i, N) = i / [1 – (P/F, i, N)]
(F/G, i, N) = (P/G, i, N)(F/P, i, N)(A/G, i, N) = (P/G, i, N)(A/P, i, N)
(F/A, g, i, N) = (P/A, g, i, N)(F/P, i, N)
