Linear Vector Spaces: Basic Definitions
Linear Vector Space
A set ![]() is called a linear vector space over the field of
is called a linear vector space over the field of ![]() if the two operations (vector addition)
if the two operations (vector addition) ![]() and (scalar multiplication)
and (scalar multiplication) ![]() are defined and satisfy the following 8 axioms:
are defined and satisfy the following 8 axioms: ![]() :
:
- Commutativity:
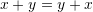
- Associativity:
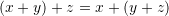
- Distributivity of vector addition over scalar multiplication:
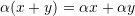
- Distributivity of scalar addition over scalar multiplication:
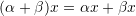
- Compatibility of scalar multiplication with field multiplication:
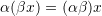
- Identity element of addition/Zero element:
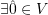 such that
such that 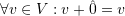
- Inverse element of addition:
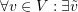 such that
such that 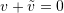 .
. 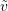 is denoted
is denoted 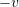
- Identity element of scalar multiplication:
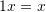
The elements of the linear vector space are called vectors, while the elements of ![]() are called scalars. In general,
are called scalars. In general, ![]() is either the field of real numbers
is either the field of real numbers ![]() or of complex numbers
or of complex numbers ![]() . For the remainder of this article,
. For the remainder of this article, ![]() is assumed to be the field of real numbers
is assumed to be the field of real numbers ![]() unless otherwise specified.
unless otherwise specified.
In the history of the development of linear vector spaces, the following statements sometimes appeared in the definition. However, the above 8 essential axioms can be used to prove them.
- The element
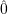 is unique.
is unique. -
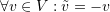 is unique.
is unique. - If
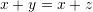 , then
, then 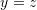 .
. 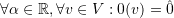 and
and 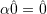 .
.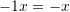
Notice that in the above definition and statements, the hat symbol was used to distinguish the zero vector ![]() from the zero scalar
from the zero scalar ![]() . However, in the future,
. However, in the future, ![]() will be used for both and it is to be understood from the context whether it is the zero vector or the zero scalar.
will be used for both and it is to be understood from the context whether it is the zero vector or the zero scalar.
Examples of linear vector spaces include the following sets:
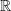
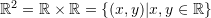
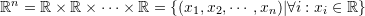
- The set
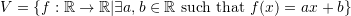 is a linear vector space!
is a linear vector space!
Subspaces
A subset ![]() of a vector space
of a vector space ![]() is called a subspace if
is called a subspace if ![]() .
.
In other words, a subset ![]() of a vector space
of a vector space ![]() is called a subspace if it is closed under both vector addition and scalar multiplication. For example, the set
is called a subspace if it is closed under both vector addition and scalar multiplication. For example, the set ![]() is a subspace of
is a subspace of ![]() (why?).
(why?).
Linear Independence
Let ![]() be a linear vector space over
be a linear vector space over ![]() . A set of vectors
. A set of vectors ![]() is called a linearly independent set of vectors if none of the vectors
is called a linearly independent set of vectors if none of the vectors ![]() can be expressed linearly in terms of the other elements in the set; i.e., the only linear combination that would produce the zero vector is the trivial combination:
can be expressed linearly in terms of the other elements in the set; i.e., the only linear combination that would produce the zero vector is the trivial combination:
![]()
Otherwise, the set is called linearly dependent.
Examples:
Consider the vector space ![]() . The set
. The set ![]() where
where ![]() and
and ![]() is linearly independent:
is linearly independent:
![]()
However, the set ![]() where
where ![]() and
and ![]() is linearly dependent:
is linearly dependent:
![]()
This means that there are multiple combinations that would give the zero vector. For example, choosing ![]() and
and ![]() would yield
would yield ![]() .
.
Notice that if the zero vector is an element of a set ![]() then, the set is automatically linearly dependent since the following non trivial combination
then, the set is automatically linearly dependent since the following non trivial combination ![]() would produce the zero vector:
would produce the zero vector:
![]()
Basis and Dimensions
A subset ![]() of a linear vector space
of a linear vector space ![]() is called a basis set if it is a set of linearly independent vectors such that
is called a basis set if it is a set of linearly independent vectors such that ![]() can be expressed as a linear combination of the elements of
can be expressed as a linear combination of the elements of ![]() . Alternatively:
. Alternatively: ![]() is a basis of
is a basis of ![]() if and only if the following two conditions are satisfied:
if and only if the following two conditions are satisfied:
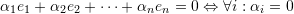
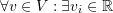 such that
such that 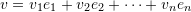
The dimension of a linear vector space ![]() is the number of elements in its basis set.
is the number of elements in its basis set.
For example ![]() is a two dimensional space, because its basis set
is a two dimensional space, because its basis set ![]() has two elements
has two elements ![]() and
and ![]() .
.
Assertion: If ![]() is a basis set of
is a basis set of ![]() , then
, then ![]() the combination
the combination ![]() is unique. i.e.,
is unique. i.e., ![]() such that
such that ![]() .
.
Proof: Use the linear independence of the basis set ![]() to prove the result.
to prove the result.
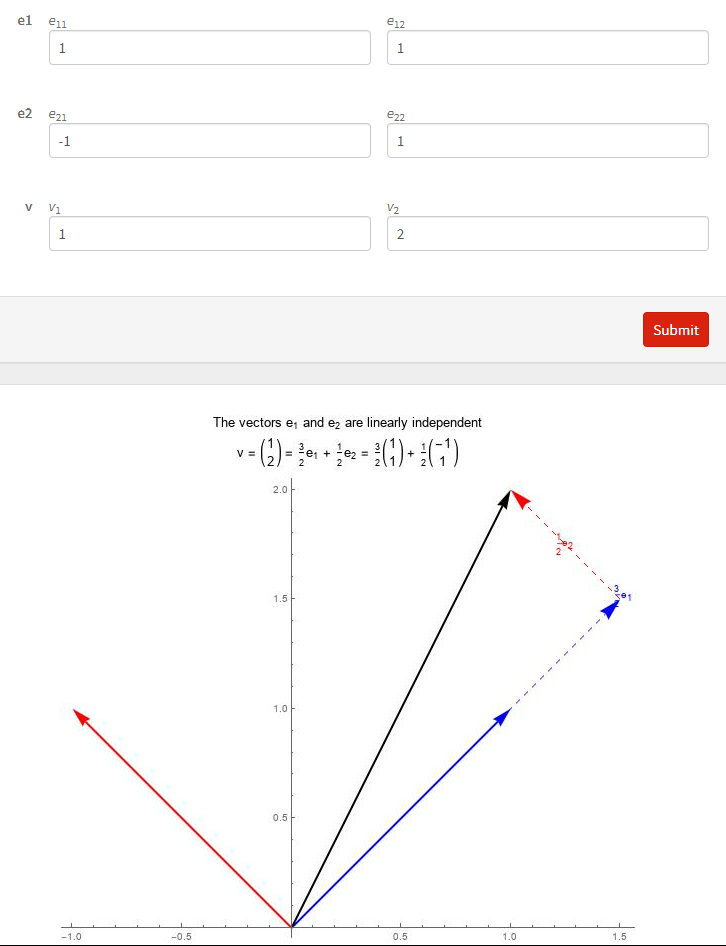
Click on the image below to interact with this example. Input the components of the vectors ![]() and
and ![]() . The tool draws the vectors
. The tool draws the vectors ![]() and
and ![]() in blue and red respectively. It identifies if the vectors are linearly dependent or linearly independent. If they are linearly independent, the tool calculates and draws the components of
in blue and red respectively. It identifies if the vectors are linearly dependent or linearly independent. If they are linearly independent, the tool calculates and draws the components of ![]() in the directions of
in the directions of ![]() and
and ![]() .
.