Special Types of Linear Maps: Orthogonal Tensors
Orthogonal Tensors
Definition
Let ![]() .
. ![]() is called an orthogonal tensor if
is called an orthogonal tensor if ![]() .
.
Properties
Using the above definition, the following five main properties of Orthogonal Tensors can be directly deduced:
Property 1: Orthogonal tensors preserve the norm (length) of vectors and the dot product between vectors:
![]() we have:
we have:
![]()
Property 2: Orthogonal tensors are invertible and  orthogonal tensor
orthogonal tensor 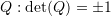 :
:
The easiest way to see this is to assume that ![]() is not invertible, which implies
is not invertible, which implies ![]() and
and ![]() while
while ![]() . This implies that
. This implies that ![]() which contradicts that
which contradicts that ![]() .
.
Another way to show that ![]() is invertible is to rely on the determinant function. Since
is invertible is to rely on the determinant function. Since ![]() , therefore,
, therefore, ![]() is invertible.
is invertible.
If ![]() then
then ![]() is called a proper orthogonal tensor, and If
is called a proper orthogonal tensor, and If ![]() then
then ![]() is called an improper orthogonal tensor.
is called an improper orthogonal tensor.
Since ![]() is invertible we can denote its inverse by
is invertible we can denote its inverse by ![]() which leads to
which leads to ![]() . Therefore:
. Therefore:
![]()
Property 3: The rows of the matrix representation of  are orthonormal:
are orthonormal:
This is a direct consequence of the fact that ![]()
Property 4: The columns of the matrix representation of  are orthonormal:
are orthonormal:
This is a direct consequence of the fact that ![]()
Property 5: The product of two orthogonal tensors is again orthogonal:
Indeed, let ![]() and
and ![]() be two orthogonal tensors, therefore:
be two orthogonal tensors, therefore:
![]()
Therefore, the product ![]() is orthogonal.
is orthogonal.
Orthogonal Tensors in 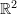
Assume that the matrix representation of an orthogonal tensor has the following representation:
![]()
Then, using the properties above, we reach the following relations between the components:
![]()
![]()
![]()
![]()
These relationships assure the existence of an angle ![]() such that
such that ![]() admits one of the the following two representations:
admits one of the the following two representations:
(1) ![]()
(2) ![]()
Proof:
Since ![]() such that:
such that: ![]() and
and ![]() .
.
Since ![]() and
and ![]() .
.
![]()
Orthogonal tensors in ![]() are either rotations or reflections. If
are either rotations or reflections. If ![]() , then
, then ![]() is called a rotation and as shown below, represents a geometric rotation of elements of
is called a rotation and as shown below, represents a geometric rotation of elements of ![]() . If
. If ![]() , then
, then ![]() is called a reflection and as shown below, represents a geometric reflection of elements of
is called a reflection and as shown below, represents a geometric reflection of elements of ![]() . It is important to note that this is only true for elements of
. It is important to note that this is only true for elements of ![]() and as will be shown later, if
and as will be shown later, if ![]() for higher dimensions,
for higher dimensions, ![]() does not necessarily represent a reflection but rather an improper rotation or “rotoinversion”.
does not necessarily represent a reflection but rather an improper rotation or “rotoinversion”.
Examples
The following are rotation matrices
![]()
The following are reflection matrices
![]()
Representation of Rotation Tensors in 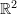
Let ![]() be the angle of rotation associated with a rotation matrix
be the angle of rotation associated with a rotation matrix ![]() . Then, given any two orthonormal vectors
. Then, given any two orthonormal vectors ![]() ,
, ![]() admits the following representation:
admits the following representation:
(3) ![]()
Proof:
Since ![]() and
and ![]() are orthonormal and
are orthonormal and ![]() , then the following relationships hold:
, then the following relationships hold:
![]()
![]()
Therefore, ![]() such that
such that
![]()
![]()
Therefore, ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} Qa&=Q(a\cdot p)p + Q(a\cdot q)q\\ &=\cos(\theta) (a\cdot p) p - \sin (\theta)(a\cdot p) q+\sin(\theta) (a\cdot q)p + \cos(\theta)(a\cdot q)q\\ &=\left((p\otimes p + q\otimes q) \cos(\theta) + (p\otimes q - q\otimes p) \sin(\theta)\right)a \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b2c03fae6c28f84238a0331f0d59b2f6_l3.png)
Therefore:
![]()
Notice that the above relationship represents a clockwise rotation of an angle ![]() . By replacing
. By replacing ![]() with
with ![]() , the counterclockwise rotation of an angle
, the counterclockwise rotation of an angle ![]() can be represented by the form:
can be represented by the form:
![]()
![]()
Geometric Representation of Rotation Tensors in 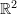
Using the matrix representation in (1) for ![]() the following example applies a rotation of
the following example applies a rotation of ![]() to the blue triangle to produce a red triangle. The angle
to the blue triangle to produce a red triangle. The angle ![]() is illustrated by the black arc. Notice that the matrix shown in (1) rotates the object clockwise!
is illustrated by the black arc. Notice that the matrix shown in (1) rotates the object clockwise!
Reflection Tensors in 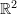
Reflection tensors represent the operation of reflecting elements in ![]() across a line of reflection.
across a line of reflection.
Assertion 1:Eigenvalues of 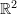 Reflection Tensors:
Reflection Tensors:
Reflection tensors in ![]() have the two eigenvalues 1 and -1 and the associated eigenvectors are orthogonal.
have the two eigenvalues 1 and -1 and the associated eigenvectors are orthogonal.
Proof:
It suffices to show that if ![]() is a reflection tensor in
is a reflection tensor in ![]() then
then ![]() .
.
Indeed:
![Rendered by QuickLaTeX.com \[ \begin{split}\det(Q-I)&=\det(Q-Q^TQ)=\det((I-Q^T)Q)\\ &=\det(Q^T-I)\det(-Q)\\ &=\det(Q^T-I)\det(Q)\\ &=\det(Q^T-I)(-1)\\ &=-\det(Q-I) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-770e3c0242e0ac2ac237b35fb76f26bf_l3.png)
Therefore:
![]()
Similarly,
![]()
Let ![]() be the eigenvectors associated with
be the eigenvectors associated with ![]() respectively. Therefore,
respectively. Therefore,
![]()
![]()
Assertion 2: Reflection tensors in 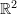 are symmetric.
are symmetric.
Proof:
This follows directly from having two orthogonal eigenvectors (See symmetric matrices).
![]()
Representation of Reflection Tensors in 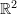
From assertion 2 above, a reflection tensor ![]() in
in ![]() has two eigenvectors
has two eigenvectors ![]() and
and ![]() associated with the eigenvalues
associated with the eigenvalues ![]() and
and ![]() respectively. Therefore,
respectively. Therefore, ![]() and
and
![]()
(4) ![]()
Matrix Representations of Reflection Tensors in 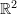
In addition to the representations (2) and (4), a reflection matrix has various other representations. Let ![]() be a reflection tensor in
be a reflection tensor in ![]() . In a coordinate system whose basis vectors are the eigenvectors
. In a coordinate system whose basis vectors are the eigenvectors ![]() and
and ![]() of
of ![]() associated with the eigenvalues
associated with the eigenvalues ![]() and
and ![]() , respectively, we denote the matrix representation of
, respectively, we denote the matrix representation of ![]() by
by ![]() which from (4) admits the form :
which from (4) admits the form :
![]()
In a general coordinate system whose basis vectors are ![]() and
and ![]() , we first apply a coordinate transformation
, we first apply a coordinate transformation ![]() into the coordinate system of the eigenvectors of
into the coordinate system of the eigenvectors of ![]() :
:
![]()
Then, ![]() admits the following form:
admits the following form:
![]()
where, ![]() and
and ![]() are the components of the vectors
are the components of the vectors ![]() and
and ![]() .
.
Notice that we can view ![]() as the perpendicular to the line of reflection since
as the perpendicular to the line of reflection since ![]() reflects
reflects ![]()
![]() . Also,
. Also, ![]() and keeps its direction
and keeps its direction ![]() , so it lies on the line of reflection. The components of
, so it lies on the line of reflection. The components of ![]() can be chosen such that
can be chosen such that ![]() while
while ![]() . In this case
. In this case ![]() admits the representation:
admits the representation:
![]()
Since ![]() and
and ![]() form an orthonormal basis in
form an orthonormal basis in ![]() then
then ![]() admits the representation:
admits the representation:
![]()
Where ![]() represents the geometric angle (with positive being the counter-clockwise direction) between the eigenvector
represents the geometric angle (with positive being the counter-clockwise direction) between the eigenvector ![]() and the basis vector
and the basis vector ![]() . Therefore,
. Therefore, ![]() admits the representation:
admits the representation:
(5) ![]()
Comparing (5) with (2) shows that ![]() . This indicates, that the angle
. This indicates, that the angle ![]() appearing in the reflection matrix representation (2) is equal to double the angle of inclination of the line of reflection.
appearing in the reflection matrix representation (2) is equal to double the angle of inclination of the line of reflection.
In the following illustrative example the effect of varying the angle of inclination of the vector ![]() , namely
, namely ![]() on the reflection of the blue triangle is shown. The vector
on the reflection of the blue triangle is shown. The vector ![]() is illustrated by the thick black arrow, while the line of reflection is represented in green.
is illustrated by the thick black arrow, while the line of reflection is represented in green. ![]() ,
, ![]() and
and ![]() are represented in black, green and red, respectively. The two equivalent matrix representations (5) and (2) are shown underneath the image.
are represented in black, green and red, respectively. The two equivalent matrix representations (5) and (2) are shown underneath the image.
Can you use the example below to find out the approximate inclination of the line of symmetry of the shown triangle?
Orthogonal Tensors in 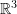
Assertion 1: Eigenvalues of Orthogonal Tensors in 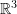 :
:
Proper and improper orthogonal tensors in ![]() have at least one eigenvalue that is equal to 1 or to -1 respectively.
have at least one eigenvalue that is equal to 1 or to -1 respectively.
Proof:
Let ![]() be a proper orthogonal tensor in
be a proper orthogonal tensor in ![]() , then
, then ![]() and
and ![]() . Therefore:
. Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} \det(Q-I)&=\det(Q-QQ^T)=\det(Q)\det(I-Q^T)=\det(-(Q^T-I))\\ &=-\det(Q^T-I)=-\det(Q-I)\\ &\Rightarrow\det(Q-I)=0 \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e666bde9811927f7d1fbb83a89aa3a58_l3.png)
Therefore, ![]() is an eigenvalue associated with every proper orthogonal tensor.
is an eigenvalue associated with every proper orthogonal tensor.
Similarly, if ![]() is an improper orthogonal tensor then:
is an improper orthogonal tensor then:
![]()
Therefore, ![]() is an eigenvalue associated with every improper orthogonal tensor.
is an eigenvalue associated with every improper orthogonal tensor.
![]()
Representation of Orthogonal Tensors in 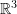
From the assertion above, if ![]() is an orthogonal tensor, then
is an orthogonal tensor, then ![]() such that
such that ![]() where the positive and negative signs correspond to a proper or an improper orthogonal tensor respectively.
where the positive and negative signs correspond to a proper or an improper orthogonal tensor respectively.
Let ![]() form with
form with ![]() a right hand oriented orthonormal basis set for
a right hand oriented orthonormal basis set for ![]() . Then, the following relationships hold with the positive and negative sign corresponding to proper and improper orthogonal tensors respectively:
. Then, the following relationships hold with the positive and negative sign corresponding to proper and improper orthogonal tensors respectively:
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() such that
such that
![]()
![]()
Therefore, ![]()
![]()
Therefore, ![]() admits the following representation:
admits the following representation:
(6) ![]()
Where ![]() is the eigenvector associated with 1 and -1 for proper and improper orthogonal tensors respectively,
is the eigenvector associated with 1 and -1 for proper and improper orthogonal tensors respectively, ![]() and
and ![]() are two vectors that form with
are two vectors that form with ![]() a right handed orthonormal basis set.
a right handed orthonormal basis set.
The following example shows a proper orthogonal (rotation) tensor in ![]() . You can vary the coordinates of the vector
. You can vary the coordinates of the vector ![]() and the angle of rotation
and the angle of rotation ![]() . The code then normalizes
. The code then normalizes ![]() (shown as a blue arrow) and finds two vectors
(shown as a blue arrow) and finds two vectors ![]() and
and ![]() (shown as red arrows) that are perpendicular to
(shown as red arrows) that are perpendicular to ![]() . Then, the proper orthogonal tensor
. Then, the proper orthogonal tensor ![]() is formed using the tensor representation in (6). The rotation is then applied to a sphere. Notice that the above form of the tensor representation rotates the sphere in a clockwise direction around
is formed using the tensor representation in (6). The rotation is then applied to a sphere. Notice that the above form of the tensor representation rotates the sphere in a clockwise direction around ![]() .
.
Unlike orthogonal tensors in ![]() , an orthogonal tensor with a determinant equal to
, an orthogonal tensor with a determinant equal to ![]() in
in ![]() is not necessarily associated with a reflection, but rather it represents a “rotoinversion” or an improper rotation.
is not necessarily associated with a reflection, but rather it represents a “rotoinversion” or an improper rotation.
The following example illustrates the action of an improper orthogonal tensor on a stack of boxes. When the angle ![]() in (6) is chosen to be zero,
in (6) is chosen to be zero, ![]() represents a reflection across the plane perpendicular to
represents a reflection across the plane perpendicular to ![]() (The plane formed by the two red arrows). The angle
(The plane formed by the two red arrows). The angle ![]() represents a rotation around
represents a rotation around ![]() and thus, the action of
and thus, the action of ![]() constitutes a rotation and an inversion and hence the term “rotoinversion”. You can change the components of the vector
constitutes a rotation and an inversion and hence the term “rotoinversion”. You can change the components of the vector ![]() and the angle
and the angle ![]() to see the effect on the resulting transformation.
to see the effect on the resulting transformation.
Matrix Representation of Orthogonal Tensors in 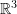
The tensor representation in (6) can be viewed in matrix form as follows. Given a normal vector ![]() such that
such that ![]() , two normalized vectors
, two normalized vectors ![]() and
and ![]() perpendicular to
perpendicular to ![]() can be chosen. Assuming that
can be chosen. Assuming that ![]() ,
, ![]() and
and ![]() form a right handed orthonormal set, then, the matrix form of a proper orthogonal tensor
form a right handed orthonormal set, then, the matrix form of a proper orthogonal tensor ![]() is given by:
is given by:
(7) 
The trace of a proper orthogonal matrix in ![]() is equal to
is equal to ![]() .
.
The matrix form of an improper orthogonal tensor ![]() is given by:
is given by:
(8) 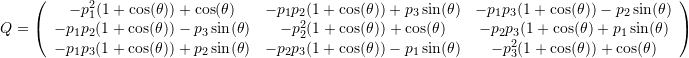
The trace of an improper orthogonal matrix in ![]() is equal to
is equal to ![]() .
.
When the angle ![]() in (8) is
in (8) is ![]() Degrees, the matrix represents a geometric reflection across the plane perpendicular to the vector
Degrees, the matrix represents a geometric reflection across the plane perpendicular to the vector ![]() . In this case, the matrix representation is given by:
. In this case, the matrix representation is given by:
(9) 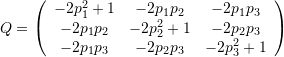
The tensor representation (6) asserts that any rotation matrix can be viewed as a rotation around an axis ![]() . Any rotation can also be viewed using Euler’s angles as consecutive rotations around each of the basis vectors of the coordinate system. Clockwise rotations with an angles
. Any rotation can also be viewed using Euler’s angles as consecutive rotations around each of the basis vectors of the coordinate system. Clockwise rotations with an angles ![]() around the basis vectors
around the basis vectors ![]() ,
, ![]() and
and ![]() are given by the following matrices
are given by the following matrices ![]() ,
, ![]() and
and ![]() , respectively:
, respectively:
![Rendered by QuickLaTeX.com \[ Q_a=\left(\begin{array}{ccc} 1& 0& 0\\ 0& \cos(\theta_a) &\sin(\theta_a)\\ 0&- \sin(\theta_a)&\cos(\theta_a)\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-42b1efe29e07bfa113b074379e37732c_l3.png)
![Rendered by QuickLaTeX.com \[ Q_b=\left(\begin{array}{ccc} \cos(\theta_b)& 0& -\sin(\theta_b)\\ 0& 1&0\\ \sin(\theta_b) & 0 &\cos(\theta_b)\end{array}\right)\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9f29f9d5938cebebcfab05aace84c356_l3.png)
![Rendered by QuickLaTeX.com \[Q_c=\left(\begin{array}{ccc} \cos(\theta_c)& \sin(\theta_c)&0\\ -\sin(\theta_c) &\cos(\theta_c)&0\\0&0&1\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-46e7162cd99400759f854e7194ea7983_l3.png)
It is important to notice that the order of rotation changes the final position of the rotated object. See the example in the rigid body rotation section.
Problems
What values for the angle ![]() would make the matrices in (7) and (8) symmetric?.
would make the matrices in (7) and (8) symmetric?.
Find the axis and angle of rotation of the rotation matrix ![]() .
.
Find the plane of inversion and the angle of rotation of the improper orthogonal matrices ![]() and
and ![]() .
.
Find the corresponding ![]() ,
, ![]() and
and ![]() if the rotation matrix
if the rotation matrix ![]() is viewed as a rotation around
is viewed as a rotation around ![]() followed by
followed by ![]() then
then ![]() .
.
Find the corresponding ![]() ,
, ![]() and
and ![]() if the rotation matrix
if the rotation matrix ![]() is viewed as a rotation around
is viewed as a rotation around ![]() followed by
followed by ![]() then
then ![]() .
.
![Rendered by QuickLaTeX.com \[ Q_1=\left(\begin{array}{ccc} {1\over3}(1+\sqrt2)&{1\over6}(2-\sqrt2-\sqrt6)&{1\over6}(2-\sqrt2+\sqrt6)\\ {1\over6}(2-\sqrt2+\sqrt6)&{1\over3}(1+\sqrt2)&{1\over6}(2-\sqrt2-\sqrt6)\\ {1\over6}(2-\sqrt2-\sqrt6)&{1\over6}(2-\sqrt2+\sqrt6)&{1\over3}(1+\sqrt2) \end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8e721f662cd185163c8192eca9c70800_l3.png)
![Rendered by QuickLaTeX.com \[ Q_2=\left(\begin{array}{ccc} {1\over3}(-1+\sqrt2)&{1\over6}(-2-\sqrt2+\sqrt6)&{1\over6}(-2-\sqrt2-\sqrt6)\\ {1\over6}(-2-\sqrt2-\sqrt6)&{1\over3}(-1+\sqrt2)&{1\over6}(-2-\sqrt2+\sqrt6)\\ {1\over6}(-2-\sqrt2+\sqrt6)&{1\over6}(-2-\sqrt2-\sqrt6)&{1\over3}(-1+\sqrt2) \end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-15b9f815237aed9c2e55fe086a606df2_l3.png)
![Rendered by QuickLaTeX.com \[ Q_3=\left(\begin{array}{ccc} {1\over3}&{-2\over3}&{-2\over3}\\ {-2\over3}&{1\over3}&{-2\over3}\\ {-2\over3}&{-2\over3}&{1\over3} \end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2619f24bab05802574cc32eaafa7b353_l3.png)
