Open Educational Resources

Linear Maps between vector spaces: Higher Order Tensors

First and Second Order Tensors in 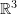\mathbb{R}^3

For the discussion in this section, we will assume a right handed orthonormal basis set B=\{e_1,e_2,e_3\} and an alternate right handed orthonormal basis set B'=\{e'_1,e'_2,e'_3\}. The two basis sets are related by the matrix Q whose components Q_{ij}=e'_i\cdot e_j.
If u\in \mathbb{R}^3 has components u_1,u_2 and u_3 in the basis set set B, and u' is the representation of u in the basis set B' with components u'_1,u'_2 and u'_3, then, these components are related with the relationship:

(1)   \begin{equation*} u'=Qu \hspace{10mm} u'_i=\sum_{j=1}^3Q_{ij}u_j \end{equation*}

Similarly, consider the tensor M:\mathbb{R}^3\rightarrow\mathbb{R}^3. If its matrix representation M has components M_{ij} when B is chosen as the basis set for \mathbb{R}^3, and if M' is the matrix representation with components M'_{ij} when B' is chosen as the basis set for \mathbb{R}^3, then, these components are related with the relationship:

(2)   \begin{equation*} M'=QMQ^T \hspace{10mm} M'_{ij}=\sum_{k,l=1}^3Q_{ik}M_{kl}Q_{jl} \end{equation*}

Vectors in \mathbb{R}^3 have 3 independent components and are called first order tensors. Linear operators from \mathbb{R}^3\rightarrow\mathbb{R}^3 have 3\times 3=9 independent components and are termed second order tensors.

Third Order Tensors in 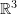\mathbb{R}^3

The linear map D:\mathbb{M}^3\rightarrow\mathbb{R}^3 where \mathbb{M}^3 is the set of all linear operators \mathbb{R}^3\rightarrow\mathbb{R}^3 is called a third order tensor.
In the following we will show how the components of D change when the orthonormal basis set for the underlying space \mathbb{R}^3 is changed.
The matrix representation of D when B is chosen as the basis set for \mathbb{R}^3 has 3\times 3 \times 3=27 independent components D_{lmn} such that \forall M\in\mathbb{M}^3,\exists u\in\mathbb{R}^3 such that:

(3)   \begin{equation*} u_l=\sum_{m,n=1}^3D_{lmn}M_{mn} \end{equation*}

Similarly, If B' is chosen as the basis set, then the components D'_{ijk} would relate the components of u' and M' as follows:

(4)   \begin{equation*} u'_i=\sum_{j,k=1}^3D'_{ijk}M'_{jk} \end{equation*}

However, premultiplying (3) with Q_{il} and summing over l produces:

(5)   \begin{equation*} \sum_{l=1}^3Q_{il}u_l=\sum_{l,m,n=1}^3Q_{il}D_{lmn}M_{mn} \end{equation*}

By replacing the components of M in (5) with the inverse of the relationship (2) and using (1) we get:

(6)   \begin{equation*} u'_i=\sum_{j,k,l,m,n=1}^3Q_{il}Q_{jm}Q_{kn}D_{lmn}M'_{jk} \end{equation*}

Comparing (4) and (6), the components D'_{ijk} are related to the components D_{lmn} by the following relationship:

(7)   \begin{equation*} D'_{ijk}=\sum_{l,m,n=1}^3Q_{il}Q_{jm}Q_{kn}D_{lmn} \end{equation*}

(7) could have also been obtained by noticing the following:

    \[ u=DM\Rightarrow Qu=Q(DM) \Rightarrow u'=Qu=Q(DM)=Q(D(Q^TM'Q))=D'M' \]

From which the relationship between the components of D and D' can be obtained.

Fourth Order Tensors in 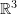\mathbb{R}^3

The linear map C:\mathbb{M}^3\rightarrow\mathbb{M}^3 where \mathbb{M}^3 is the set of all linear operators \mathbb{R}^3\rightarrow\mathbb{R}^3 is called a fourth order tensor.
In the following we will show how the components of C change when the orthonormal basis set for the underlying space \mathbb{R}^3 is changed.
The matrix representation of C when B is chosen as the basis set for \mathbb{R}^3 has 3\times 3 \times 3\times 3=81 independent components C_{mnop} such that \forall M\in\mathbb{M}^3,\exists N\in\mathbb{M}^3 such that:

(8)   \begin{equation*} N_{mn}=\sum_{o,p=1}^3C_{mnop}M_{op} \end{equation*}

Similarly, If B' is chosen as the basis set, then the components C'_{ijkl} would relate the components of M' and N' as follows:

(9)   \begin{equation*} N'_{ij}=\sum_{k,l=1}^3C'_{ijkl}M'_{kl} \end{equation*}

However, premultiplying (8) with the components Q_{im} and Q_{jn} and summing over m and n results in:

(10)   \begin{equation*} \sum_{m,n=1}^3Q_{im}Q_{jn}N_{mn}=\sum_{m,n,o,p=1}^3Q_{im}Q_{jn}C_{mnop}M_{op} \end{equation*}

By replacing the components of M in (10) with the inverse of the relationship (2) and using 2 we get:

(11)   \begin{equation*} N'_{ij}=\sum_{k,l,m,n,o,p=1}^3Q_{im}Q_{jn}Q_{ko}Q_{lp}C_{mnop}M'_{kl} \end{equation*}

Comparing (11) and (9), the components C'_{ijkl} are related to the components C_{mnop} by the following relationship:

(12)   \begin{equation*} C'_{ijkl}=\sum_{m,n,o,p=1}^3Q_{im}Q_{jn}Q_{ko}Q_{lp}C_{mnop} \end{equation*}

(12) could have also be obtained by noticing the following:

    \[ N=CM\Rightarrow QNQ^T=Q(CM)Q^T \Rightarrow N'=QNQ^T=Q(CM)Q^T=Q(C(Q^TM'Q))Q^T=C'M' \]

From which the relationship between the components of C and C' can be obtained.

Leave a Reply

Your email address will not be published.