Open Educational Resources

Linear Vector Spaces: Euclidean Vector Spaces

In these pages, a Euclidean Vector Space is used to refer to an n dimensional linear vector space equipped with the Euclidean norm, the Euclidean metric and the Euclidean dot product functions. These functions allow the definition of orthonormal basis sets, orthogonal projections and the cross product operation.

Orthonormal Basis

An orthonormal basis set is a basis set whose vectors satisfy two conditions. The first condition is that the vectors in the basis set are orthogonal to each other and the second condition is that each vector has a unit norm.

Let B=\{e_1,e_2,\cdots,e_n\} be an orthonormal basis set for \mathbb{R}^n. Since B is a basis set, we know that \forall x\in\mathbb{R}^n:x=x_1e_1+x_2e_2+\cdots+x_ne_n. Since B is an orthonormal basis set, the components x_i can be obtained using the dot product so that:

    \[ x=(x\cdot e_1)e_1+(x\cdot e_2)e_2+\cdots+(x\cdot e_n)e_n \]

Orthogonal Projection

The dot product structure allows the definition of orthogonal projections. Given a vector 0\neq y\in\mathbb{R}^n, the orthogonal projection allows the unique additive decomposition of any vector x\in\mathbb{R}^n into two vectors a and b where a is in the direction of y and b is orthogonal to y. The vector a is called the orthogonal projection of x onto y. It can be easily shown that a and b are equal to:

    \[ a=\left({x\cdot y \over \|y\|^2}\right)y\hspace{10mm} b=x-a \]

Proof

Let x=a+b. Since a is in the direction of y, then \exists \alpha\in\mathbb{R} such that a=\alpha y. Since b is orthogonal to y we have:
0 = b\cdot y = (x-a)\cdot y = (x-\alpha y )\cdot y \Rightarrow \alpha={x\cdot y \over \|y\|^2}\Rightarrow a=\left({x\cdot y \over \|y\|^2}\right)y.

\blacksquare

In the following tool, enter the components of the vectors x and y. The tool draws the vectors x and y in black and blue respectively. The vectors a=\alpha y and b=x-a are calculated as above and drawn using dotted black arrows. Notice that the orthogonal projection of x onto y is not equal to the orthogonal projection of y onto x.

Cross Product in 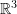\mathbb{R}^3

The structure of the Euclidean vector space \mathbb{R}^3 allows the definition of the cross product operation. This is a unique map that gives the vector perpendicular to any two linearly independent vectors.

The cross product is the operation: \times:\mathbb{R}^3\times\mathbb{R}^3\rightarrow\mathbb{R}^3 satisfying the following properties \forall u,v,w \in\mathbb{R}^3,\forall \alpha\in\mathbb{R}:

1. Denoting z:=u\times v, the resulting vector z is orthogonal to the two vectors u and v

    \[ z\cdot u=z\cdot v = 0 \]

2. The operation is skewsymmetric:

    \[ u\times v= -v \times u \]

3. The operation is distributive over addition:

    \[ u\times(v+w)=u\times v + u\times w \]

4. The operation is compatible with scalar multiplication:

    \[ (\alpha u)\times v=\alpha(u\times v)=u\times(\alpha v) \]

5. \|z\|^2=z\cdot z=\|u\|^2\|v\|^2-(u\cdot v)^2=(u\cdot u)(v \cdot v)-(u\cdot v)^2
The last property ensures that the norm of the resulting vector z is equal to the area of the parallelogram formed by the two vectors u and v.

The cross product operation is defined above using its algebraic properties. Equivalently, the cross product can be defined as follows, given u, v\in\mathbb{R}^3:

    \[ z:=u\times v = \|u\|\|v\|\sin\theta n \]

where \theta is the geometric angle between u and v while n is a unit vector orthogonal to both a and b in the direction given by the right-hand rule.

In the following, the algebraic properties of the cross product are used to show the traditional properties of the cross product given an orthonormal basis set B=\{e_1,e_2,e_3\}:

The cross product of the basis vectors

    \[ e_1\times e_2=\pm e_3\hspace{10mm}e_2\times e_3=\pm e_1\hspace{10mm}e_3\times e_1=\pm e_2 \]

Where the positive sign is used to indicate a right-handed orientation.

Proof

This is straightforward from properties 1 and 5 above. From property 1, since z=e_1\times e_2 is perpendicular to both e_1 and e_2, then z=\alpha e_3.
To find the value of \alpha, we use the last property as follows:

    \[ \|z\|^2=\alpha^2=(e_1\cdot e_1)(e_2\cdot e_2)-(e_1\cdot e_2)^2=1\Rightarrow \alpha=\pm 1 \]

\blacksquare

The cross product of linearly dependent vectors

    \[ u\times v = 0 \Leftrightarrow u=0 \text{ or } v=0 \text{ or } u=\alpha v \]

Indicating that if u and v are linearly dependent, then their cross product is equal to zero.

Proof

We first assume that either u=0 \text{ or } v=0 \text{ or } u=\alpha v. From property 4 above, if u or v is equal to 0 then, the cross product is equal to the zero vector. From property 5, if u=\alpha v, then:

    \[ \|z\|^2=(\alpha v\cdot \alpha v)(v \cdot v)-(\alpha v\cdot v)^2=\alpha^2 \left((v\cdot v)^2-(v\cdot v)^2\right)=0\Rightarrow z=0 \]

Then, we assume that u\times v=0 and that u and v are non-zero vectors and that u and v are not linearly dependent. Using the orthogonal projection defined above, \exists \alpha\in\mathbb{R} and 0\neq b\in\mathbb{R}^3 such that u=\alpha v +b and b\cdot v=0. Then:

    \[ \|z\|^2=(u\cdot u)(v \cdot v)-(u\cdot v)^2=((\alpha v + b)\cdot (\alpha v + b))(v \cdot v)-((\alpha v + b)\cdot v)^2=(b\cdot b)(v\cdot v)\neq 0 \]

which is a contradiction, therefore, u=\alpha v with \alpha = {u\cdot v \over (v\cdot v)}

\blacksquare

The explicit representation of the cross product

    \[ u\times v = (u_2v_3-u_3v_2)e_1+(u_3v_1-u_1v_3)e_2+(u_1v_2-u_2v_1)e_3 \]

Proof

This is a direct consequence of property 3 above and the cross product of the basis vectors result.

\blacksquare

The triple product u\cdot (v\times w)

The triple product of any three vectors u,v,w\in\mathbb{R}^3 satisfies:

    \[ u\cdot (v\times w)=v\cdot (w\times u)=w\cdot (u\times v)=-u\cdot (w\times v)=-v\cdot (u\times w)=-w\cdot (v\times u) \]

Proof

This is a direct consequence of properties 1 and 2 above as follows:

    \[ (u+v)\cdot ((u+v)\times w) =0\Rightarrow u\cdot(v\times w)+v\cdot(u\times w)=0\Rightarrow u\cdot (v\times w)=-v\cdot (u\times w)=v\cdot (w\times u) \]

The remaining equalities can be proven similarly

\blacksquare

The triple product u\cdot (v\times w) of linearly dependent vectors

The triple product of any three vectors u,v,w\in\mathbb{R}^3 satisfies:

    \[ u\cdot (v\times w)=0 \Leftrightarrow u,v,w \text{ are linearly dependent} \]

Proof

The one direction is straight forward, if u,v,w are linearly dependent, then there is a non trivial combination such that: \alpha_1u+\alpha_2v+\alpha_3w=0. Without loss of generality, we can assume that \alpha_1\neq 0 then, from properties 1 and 3 we get:

    \[ \left(\frac{\alpha_2}{\alpha_1}v+\frac{\alpha_3}{\alpha_1}w\right)\cdot(v\times w)=\frac{\alpha_2}{\alpha_1}v\cdot(v\times w)+\frac{\alpha_3}{\alpha_1}w\cdot(v\times w)=0 \]

In the opposite direction we will argue by contradiction. Assuming that u, v and w are linearly independent, then they form a basis in \mathbb{R}^3. Assuming that u\cdot (v\times w)=0, then, v\times w is orthogonal to u. In addition, from property 1, v\times w is orthogonal to v and w. Therefore, v\times w is orthogonal to every vector in the space including itself! This is a contradiction (why?). Therefore, u,v and w are linearly dependent.

\blacksquare

The triple product u\cdot (v\times w) of orthonormal vectors

If u,v,w are orthonormal then:

    \[ u\cdot (v\times w)=\pm 1 \]

Proof

Similar to the proof for the cross product of the basis vectors.

\blacksquare

Exercise:

Show that \forall u,v\in\mathbb{R}^3:\|u\times v\|=\|u\|\|v\|\sin\theta. Where \theta is the angle between u and v.

The following tool calculates the cross product z=x\times y. The vectors x, y and z are drawn in blue, red and black respectively. The plane joining x and y is highlighted. Notice that z is orthogonal to that plane.

 

Leave a Reply

Your email address will not be published.