Engineering at Alberta Courses » Skewsymmetric Tensors

Special Types of Linear Maps: Skewsymmetric Tensors

Skewsymmetric Tensors Definition

Let $W:\mathbb{R}^n\rightarrow\mathbb{R}^n$ . $W$ is called a skewymmetric tensor if $W^T=-W$ .
The following properties can be naturally deduced from the definition of skewsymmetric tensors:

In component form, the matrix representation of 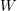$W$ is such that 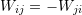$W_{ij}=-W_{ji}$ . Therefore, the diagonal compoments are all zero.
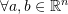$\forall a,b\in\mathbb{R}^n$ we have:

$Wa\cdot b=-a\cdot Wb$

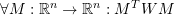$\forall M:\mathbb{R}^n\rightarrow\mathbb{R}^n:M^TWM$ is skewsymmetric. In particular, if 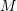$M$ is an orthogonal matrix associated with a coordinate transformation, then the matrix representation of 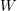$W$ stays skewsymmetric in any coordinate system.
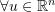$\forall u\in\mathbb{R}^n$ we have 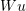$Wu$ is orthogonal to $u$ . Indeed:

(1) $\begin{equation*} Wu\cdot u=-u\cdot Wu\Rightarrow Wu\cdot u =0 \end{equation*}$

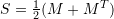Every tensor $M:\mathbb{R}^n\rightarrow\mathbb{R}^n$ can be decomposed into two additive components, a symmetric tensor $S={1\over 2} (M+M^T)$ and a skewsymmetric tensor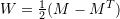 $W={1\over 2} (M-M^T)$

The following is an example of the matrix representation of a skew symmetric tensor $W:\mathbb{R}^3\rightarrow\mathbb{R}^3$ :

$W=\left( \begin{array}{ccc} 0&12&13\\ -12&0&23\\ -13&-23&0 \end{array} \right)$

Skewsymmetric Tensors in 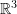$\mathbb{R}^3$

Properties

Skewsymmetric tensors in $\mathbb{R}^3$ represent the instantaneous rotation of objects around a certain axis. In fact, for every skewsymmetric tensor $W:\mathbb{R}^3\rightarrow\mathbb{R}^3$ , there exists a vector $p\in\mathbb{R}^3$ , such that $\forall a\in\mathbb{R}^3:Wa=p \times a$ . In other words, the action of $W$ on any vector $a$ can be represented as the cross product between a fixed vector $p$ and $a$ . We will show this by first looking at one of the eigenvalues of a skewsymmetric tensor:

Assertion 1:

$\lambda=0$ is an eigenvalue for any skewsymmetric tensor $W:\mathbb{R}^3\rightarrow\mathbb{R}^3$

Proof:

Note that this result applies to any vector space with dimensions $n$ when $n$ is odd.
Since the characteristic function of $W$ , namely $\det(W-\lambda I)$ produces a polynomial of a third degree, it has at least one real eigenvalue. Therefore, there exists a corresponding eigenvector, say $p\in \mathbb{R}^3$ . However, from (1), $Wp$ is orthogonal to $p$ which means that $\lambda p$ is orthogonal to $p$ , but $p$ cannot be the zero vector, so, $Wp$ has to be the zero vector, therefore, $\lambda=0$ . These statements can also be written as follows:

$Wp=\lambda p\Rightarrow 0=Wp\cdot p = \lambda p \cdot p = \lambda (p \cdot p) \Rightarrow \lambda =0$

Notice that this implies that $W$ is not invertible!

Assertion 2:

The action of a skewsymmetric tensor is equivalent to the cross product operation in the following manner: If $W:\mathbb{R}^3\rightarrow\mathbb{R}^3$ is a skewsymmetric tensor and $p\in\mathbb{R}^3$ is the normalized eigenvector associated with the eigenvalue $\lambda=0$ . If $p,q,r$ form a right handed orthonormal basis set in $\mathbb{R}^3$ , then $\forall a\in \mathbb{R}^3$ :

$Wa=\omega p \times a$

where $\omega=Wq\cdot r$

Proof:

First we show that $Wq=\omega r$ and $Wr=-\omega q$ . To show this, we will use the fact that $Wp=0$ and that $Wq\cdot r=-q\cdot Wr$ .
Indeed, since $B=\{p,q,r\}$ form an orthonormal basis set, then, $\exists \alpha, \beta, \gamma\in\mathbb{R}$ such that $Wq=\alpha p + \beta q +\gamma r$ , the components $\alpha, \beta$ and $\gamma$ can be found by taking the dot product between $Wq$ and the vectors $q, p$ and $r$ .

$\alpha=Wq\cdot p = q\cdot W^Tp = -q\cdot Wp = 0$

$\beta=Wq\cdot q = q\cdot W^Tq = -q\cdot Wq = 0$

$\gamma=Wq\cdot r = \omega$

Therefore:

$Wq = \omega r$

Similarly,

$Wr =- \omega q$

Finally we show that $\forall a\in \mathbb{R}^3: Wa=\omega p \times a$ . Indeed, since $B=\{p,q,r\}$ form a right handed orthonormal basis set, then, $\exists a_1, a_2, a_3\in\mathbb{R}$ such that $a=a_1p+a_2q+a_3r$ .
Therefore:

$Wa=a_1Wp+a_2Wq+a_3Wr=a_2\omega r-a_3\omega q$

Also:

$\omega p \times a=\omega p \times(a_1p+a_2q+a_3r)=\omega (a_1 p \times p+a_2p\times q+a_3p\times r)=a_2\omega r-a_3\omega q$

Therefore:

(2) $\begin{equation*} Wa=\omega p \times a \end{equation*}$

The vector $\omega p$ is called the axial vector of $W$ .

$\blacksquare$

The matrix representation of a skewsymmetric tensor in 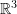$\mathbb{R}^3$

In an arbitrary coordinate system defined by the orthnormal basis set $B=\{e_1,e_2,e_3\}$ , the matrix representation of a skewsymmetric tensor $W:\mathbb{R}^3\rightarrow\mathbb{R}^3$ has the following form:

$W= \left(\begin{array}{ccc} 0 & W_{12}&W_{13}\\ -W_{12} & 0&W_{23}\\-W_{13} & -W_{23}&0\end{array}\right)$

The axial vector of $W$ adopts the following form (Why?):

$\omega p = \left(\begin{array}{cc} -W_{23}\\ W_{13}\\-W_{12}\end{array}\right)$

The relationship between the skewsymmetric tensors and rotations in 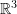$\mathbb{R}^3$

Skewsymmetric matrices with real number entries are the slopes of real orthogonal matrices around the identity matrix, i.e., skewsymmetric matrices can be considered as infinitesimal rotations.
For example, consider the following rotation matrix:

$Q=\left( \begin{array}{ccc} \cos(\omega t)&-\sin(\omega t)&0\\ \sin(\omega t)&\cos(\omega t)&0\\ 0&0&1 \end{array} \right)$

Where, $t$ is time. The matrix $Q$ is a function of time and describes the counterclockwise rotation of objects in $\mathbb{R}^3$ around the vector $p=\{0,0,1\}$ with an angular velocity $\omega$ .
The time derivative of $Q$ , namely $\dot{Q}$ has the form:

$\dot{Q}=\omega \left( \begin{array}{ccc} -\sin(\omega t)&-\cos(\omega t)&0\\ \cos(\omega t)&-\sin(\omega t)&0\\ 0&0&1 \end{array} \right)$

When $t=0$ , $Q$ is the identity matrix $I$ and $\dot{Q}$ is then a skewsymmetric matrix:

$\dot{Q}=\left( \begin{array}{ccc} 0&-\omega&0\\ \omega&0&0\\ 0&0&0 \end{array} \right)$

$\dot{Q}$ describes the velocity of counterclockwise rotation around the axial vector $p=\{0,0,1\}$ with an angular velocity $\omega$ .

We can now generalize this for every rotation matrix.

Assertion:

For very small rotations, the rate of change of a rotation tensor is represented by a skewsymmetric tensor

Proof:

Let $Q:\mathbb{R}^3\rightarrow\mathbb{R}^3$ be a rotation tensor that varies as a function of time. Assume also, that at $t=0$ , the rotation angle $\theta=0$ , i.e., $Q|_{t=0}=I$ .
Then:

$QQ^T=I\Rightarrow Q\dot{(Q^T)}+\dot{Q}Q^T=0$

Where $\dot{Q}$ is the time derivative of $Q$ . For small rotations, or in other words when $t=0$ and $Q|_{t=0}=I$ :

$\dot{(Q^T)}|_{t=0}=-\dot{Q}|_{t=0}$

Therefore, $\dot{Q}|_{t=0}$ is a skewsymmetric tensor.
Notice that the same proof applies if instead we take the derivative of $Q$ with respect to $\theta$ , i.e., ${\partial Q \over \partial \theta}$ is a skewsymmetric tensor at $Q=I$ .

$\blacksquare$

The above asserts that the time derviative of a rotation tensor at small rotations is a skewsymmetric tensor.
We will now look at the skewsymmetric tensors themselves to show that:

Assertion:

Every skewsymmetric tensor represents the speed of rotation (the rate of change of a rotation matrix).

Proof:

The relationship (2) asserts that the action of a skewsymmetric tensor on a vector $a\in\mathbb{R}^3$ corresponds to the operation $\omega p \times a$ .
Recall that if an object is rotating counterclockwise with an angular velocity $\omega$ around a unit vector $p$ , then the velocity vector of each point (represented by a vector $a$ ) on the object will be equal to $\omega p \times a$ .
i.e., a skewsymmetric tensor $W$ describes the angular velocity around its real eigenvector $p$ . Recall that this eigenvector corresponds to the eigenvalue $\lambda=0$ .

Consider, the counterclockwise infinitesimal rotation around a normalized vector $p\in\mathbb{R}^3$ with angular velocity $\omega$ . The infinitesimal angle of rotation is equal to $d\theta=\omega dt$ where $dt$ is an infinitesimal time duration.
The infinitesimal rotation is then described by the skewsymmetric tensor $Wdt$ . The new position of every vector $a\in\mathbb{R}^3$ after rotating would be equal to its original position plus a small increment $(Wdt) a$ corresponding to its infintesimal angular rotation. Thus, the vector $a$ is transformed into the vector $a+Wdta=(I+Wdt)a$ . Setting