Engineering at Alberta Courses » Additional Definitions and Properties of Linear Maps

Linear Maps between vector spaces: Additional Definitions and Properties of Linear Maps

Matrix Transpose

Let $M:\mathbb{R}^n\rightarrow\mathbb{R}^m$ be a linear map. If $M$ is the matrix representation after choosing particular orthonormal basis sets for the underlying spaces, then, the transpose of $M$ or $M^T$ , is a map $M^T:\mathbb{R}^m\rightarrow\mathbb{R}^n$ whose columns are the rows of $M$ .
In component form, this means:

$(M^T)_{ij}=M_{ji}$

The above definition relies on components. Another equivalent but more convenient definition is as follows.
Let $M:\mathbb{R}^n\rightarrow\mathbb{R}^m$ be a linear map. Then, $M^T:\mathbb{R}^m\rightarrow\mathbb{R}^n$ is the unique linear map that satisfies:

$\forall u\in\mathbb{R}^n,\forall v\in\mathbb{R}^m: Mu\cdot v=u\cdot M^Tv$

Any of the above two definitions can be used to show the following facts about the transpose of square matrices. $\forall N,M:\mathbb{R}^n\rightarrow\mathbb{R}^n$

$(NM)^T=M^TN^T \hspace{10mm} (N+M)^T=N^T+M^T \hspace{10mm} (NM^T)_{ij}=\sum_{k=1}^n N_{ik}M_{jk}$

Notice that since the determinant of a square matrix $M:\mathbb{R}^n\rightarrow\mathbb{R}^n$ is the same whether we consider the rows or the columns, then:

$\det(M)=\det(M^T)$

For example

$A= \left( \begin{array}{ccc} 1&9&3\\ 2&9&5 \end{array} \right) \hspace{10mm} \Rightarrow \hspace{10mm} A^T= \left( \begin{array}{cc} 1&2\\ 9&9\\ 3&5 \end{array} \right)$

$B= \left( \begin{array}{ccc} 1&9&2\\ 4&1&3\\ 5&2&7 \end{array} \right) \Rightarrow \det(B)=-110 \hspace{10mm} B^T= \left( \begin{array}{ccc} 1&4&5\\ 9&1&2\\ 2&3&7 \end{array} \right) \Rightarrow \det(B^T)=-110$

Matrix Inverse

Let $M:\mathbb{R}^n\rightarrow\mathbb{R}^n$ be a linear map. The following are all equivalent:

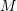$M$ is invertible
The rows of the matrix representation of 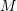$M$ are linearly independent
The kernel of the 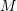$M$ contains only the zero vector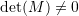
$\det(M)\neq 0$

In this case, the inverse of $M$ is denoted $M^{-1}$ and satisfies:

$MM^{-1}=M^{-1}M=I$

Notice that $M^{-1}$ is unique, because if there is another matrix $B$ such that $MB=I$ , then $M^{-1}MB=M^{-1}\Rightarrow B=M^{-1}$ .
Notice also that if $\exists A,B$ such that $MA=I$ and $BM=I$ , then, $A=A\Rightarrow (BM)A=A \Rightarrow B(MA)=A\Rightarrow B=A$ .

If the linear maps $A$ and $B$ are invertible, then it is easy to show that $AB$ is also invertible and:

$(AB)^{-1}=B^{-1}A^{-1}$

Matrix Inverse in 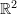$\mathbb{R}^2$

Consider the matrix:

$M=\left( \begin{array}{cc} a_1&a_2\\ b_1&b_2 \end{array} \right)$

Then, the inverse of $M$ can be shown to be:

$M^{-1}={1\over (a_1b_2-a_2b_1)}\left( \begin{array}{cc} b_2&-a_2\\ -b_1&a_1 \end{array} \right) ={1\over \det(M)}\left( \begin{array}{cc} b_2&-a_2\\ -b_1&a_1 \end{array} \right)$

Try it out, input the values of the matrix $M$ and press evaluate to calculate its inverse.

Matrix Inverse in 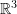$\mathbb{R}^3$

Consider the matrix:

$M=\left( \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right)$

If $a=\{a_1,a_2,a_3\}$ , $b=\{b_1,b_2,b_3\}$ and $c=\{c_1,c_2,c_3\}$ , then, the inverse of $M$ can be shown to be:

$M^{-1}={1\over (a\cdot (b \times c))}\left( \begin{array}{ccc} \vdots&\vdots&\vdots\\ b\times c&c\times a & a \times b\\ \vdots&\vdots&\vdots \end{array} \right) ={1\over \det(M)}\left( \begin{array}{ccc} \vdots&\vdots&\vdots\\ b\times c&c\times a & a \times b\\ \vdots&\vdots&\vdots \end{array} \right)$

Try it out, input the values of the matrix $M$ and press evaluate to calculate its inverse.

Invariants

Consider $\mathbb{R}^n$ with the two orthonormal basis sets $B=\{e_i\}_{i=1}^n$ and $B'=\{e'_i\}_{i=1}^n$ with a coordinate transformation matrix $Q$ such that $Q_{ij}=e'_i\cdot e_j$ .
Clearly, the components of vectors and the matrices representing linear operators change according to the chosen coordinate system (basis set). Invariants are functions of these components that do not change whether $B$ or $B'$ is chosen as the basis set.
The invariants usually rely on the fact that $QQ^T=I$ .

Vector Invariants

Vector Norm

A vector $u\in\mathbb{R}^n$ has the representation $u$ with components $u_i$ when $B$ is the basis set. Alternatively, it has the representation $u'$ with components $u'_i$ when $B'$ is the basis set.
The norm of the vector $u$ is an invariant since it is equal whether we use $B$ or $B'$ .
The norm of $u$ when $B$ is the basis set:

$\|u\|^2=u\cdot u$

The norm of $u'$ is also equal to the norm of $u$ :

$\|u'\|^2=u'\cdot u'=Qu\cdot Qu=u\cdot Q^TQu=u\cdot u = \|u\|^2\Rightarrow\|u'\|=\|u\|$

Vector Dot Product

Similarly, the dot product between two vectors $u,v\in\mathbb{R}^n$ is invariant:

$u\cdot v=u\cdot Q^TQv=Qu\cdot Qv=u'\cdot v'$

Matrix Invariants in 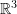$\mathbb{R}^3$

We will restrict our discusion of invariants when the underlying space is $\mathbb{R}^3$ . A linear operator $M:\mathbb{R}^3\rightarrow\mathbb{R}^3$ has the matrix representation $M$ with components $M_{ij}$ when $B$ is the basis set.
Alternatively, it has the representation $M'=QMQ^T$ with components $M'_{ij}$ when $B'$ is the basis set. The following are some invariants of the matrix $M$ :

First Invariant, Trace

The trace of $M$ or $I_1(M)$ is defined as:

$I_1(M)=\text{Tr}(M)=\sum_{i=1}^3M_{ii}$

$\text{Tr}(M)$ is invariant for if we consider the components in $B'$ :

$I_1(M')=\sum_{i=1}^3M'_{ii}=\sum_{i,j,k=1}^3Q_{ij}M_{jk}Q_{ik}=\sum_{j,k=1}^3\delta_{jk}M_{jk}=\sum_{j=1}^3M_{jj}=I_1(M)$

It is straight forward from the definition to show that $\forall M,N\in\mathbb{M}^3,\forall\alpha\in\mathbb{R}$ :

$I_1(\alpha M)=\alpha I_1(M)\hspace{10mm}I_1(M+N)=I_1(M)+I_1(N)$

The above definition for the first invariant depends on the components in a given coordinate system. Another definition according to P. Chadwick that is independent of a coordinate system is given as follows:

$\begin{split} I_1(M)&=Me_1\cdot e_1+Me_2\cdot e_2+Me_3\cdot e_3\\ &=Me_1\cdot (e_2\times e_3)+e_1\cdot (Me_2\times e_3)+e_1\cdot (e_2\times Me_3)\\ &=\frac{Ma\cdot (b\times c)+a\cdot (Mb\times c)+a\cdot (b\times Mc)}{a\cdot(b\times c)} \end{split}$

where, $a, b$ and $c \in\mathbb{R}^3$ are three arbitrary linearly independent vectors. Use the components of $a, b$ and $c$ to verify that the two definitions are equivalent.

Second Invariant

The second invariant $I_2(M)$ is defined as:

$I_2(M)={1\over 2}(\left(I_1(M)\right)^2-I_1(MM))$

Clearly, since $I_1(M)$ is invariant, so is $I_2(M)$ :

$\begin{split} I_2(M')&={1\over 2}(\left(I_1(M')\right)^2-I_1(M'M'))={1\over 2}(\left(I_1(QMQ^T)\right)^2-I_1(QMMQ^T)\\ &={1\over 2}(\left(I_1(M)\right)^2-I_1(MM)\\ &=I_2(M) \end{split}$

Another definition for the second invariant according to P. Chadwick that is independent of a coordinate system is given as follows:

$\begin{split} I_2(M)&=Me_1\cdot (Me_2\times e_3)+Me_1\cdot (e_2\times Me_3)+e_1\cdot (Me_2\times Me_3)\\ &=\frac{Ma\cdot (Mb\times c)+Ma\cdot (b\times Mc)+a\cdot (Mb\times Mc)}{a\cdot(b\times c)} \end{split}$

where, $a, b$ and $c \in\mathbb{R}^3$ are three arbitrary linearly independent vectors. Use the components of $a, b$ and $c$ to verify that the two definitions are equivalent.

Third Invariant, the Determinant

The third invariant $I_3(M)$ is defined as the determinant of the matrix $M$ ;

$I_3(M)=\det(M)$

Clearly, $I_3(M)$ is invariant:

$I_3(M')=\det(QMQ^T)=\det(Q)\det(Q^T)\det(M)=\det(M)=I_3(M)$

Another definition for the third invariant according to P. Chadwick that is independent of a coordinate system is given as follows:

$\begin{split} I_3(M)&=Me_1\cdot (Me_2\times Me_3)\\ &=\frac{Ma\cdot (Mb\times Mc)}{a\cdot(b\times c)} \end{split}$

where, $a, b$ and $c \in\mathbb{R}^3$ are three arbitrary linearly independent vectors. Use the components of $a, b$ and $c$ to verify that the two definitions are equivalent.
The trace (first invariant) and determinant (third invariant) of a matrix $M\in\mathbb{M}^3$ are related as follows:

$\det(M)=\frac{1}{6}\left(\left(I_1(M)\right)^3-3I_1\left(M^2\right)I_1(M)+2I_1\left(M^3\right)\right)$

Eigenvalues are Invariants

The eigenvalues of the matrices $M$ and $M'=QMQ^T$ are the same (why?).
It is worth mentioning that the three invariants mentioned above appear naturally in the characteristic equation of $M$ :

$\det(M-\lambda I)=\lambda^3-I_1(M)\lambda^2+I_2(M)\lambda-I_3(M)=0$

Input the components of a matrix $M$ in the following tool and three angles for coordinate transformation. The tool then calculates the three matrix invariants along with the eigenvalues and eigenvectors in both coordinate systems. As expected, the invariants and the eigenvalues are the same. However, the components of the eigenvectors are different. The vectors themselves are the same, but the components are different according to the relationship $ev'=Q (ev)$ .

Cayley-Hamilton Theorem

The Cayley-Hamilton Theorem is an important theorem in linear algebra that asserts that a matrix satisfies its characteristic equation. In other words, let $A\in\mathbb{M}^n$ . The eigenvalues of $A$ are those that satisfy:

$\det\left(\lambda I-A\right)=\lambda^n+c_{n-1}\lambda^{n-1}+c_{n-2}\lambda^{n-2}+\cdots+c_1\lambda + c_0=0$

where $c_i$ are polynomial expressions of the entries of the matrix $A$ . In particular, $c_0=(-1)^n\det{(A)}$ . Then, the Cayley-Hamilton Theorem asserts that:

$A^n+c_{n-1}A^{n-1}+c_{n-2}A^{n-2}+\cdots+c_1A + c_0 I=0$

The first equation is a scalar equation which is a polynomial expression of the variable $\lambda$ . However, the second equation is a matrix equation in which the sum of the given matrices gives the 0 matrix. Without attempting a formal proof for the theorem, in the following we will show how the theorem applies to $\mathbb{M}^2$ and $\mathbb{M}^3$ .

Two Dimensional Matrices

Consider the matrix:

$M= \left( \begin{array}{cc} M_{11}&M_{12}\\ M_{21}&M_{22} \end{array} \right)$

Therefore, the characteristic equation of $M$ is given by:

$\det{\left(\lambda I - M\right)}=\det{\left(\begin{array}{cc}\lambda - M_{11}&-M_{12}\\-M_{21}&\lambda- M_{22}\end{array}\right)}=0$

I.e.,

$\begin{split} \det{\left(\lambda I - M\right)} &= \lambda^2 - \left(M_{11}+M_{22}\right)\lambda + \left(M_{11}M_{22}-M_{12}M_{21}\right)\\ &=\lambda^2-\text{Tr}(M)\lambda+\det{M}\\ &=0 \end{split}$

The matrix $M$ satisfies the characteristic equation as follows:

$M^2-\text{Tr}(M)M+(\det{M})I=\left( \begin{array}{cc} 0&0\\ 0&0 \end{array} \right)$

Where:

$M^2=\left( \begin{array}{cc} M_{11}^2+M_{12}M_{21}&M_{11}M_{12}+M_{22}M_{12}\\ M_{11}M_{21}+M_{21}M_{22}&M_{12}M_{21}+M_{22}^2 \end{array} \right)$

$\text{Tr}(M)M=\left( \begin{array}{cc} M_{11}^2+M_{22}M_{11}&M_{11}M_{12}+M_{22}M_{12}\\ M_{11}M_{21}+M_{22}M_{21}&M_{11}M_{22}+M_{22}^2 \end{array} \right)$

and

$(\det{M})I= \left( \begin{array}{cc} M_{11}M_{22}-M_{12}M_{21}&0\\ 0&M_{11}M_{22}-M_{12}M_{21} \end{array} \right)$

The following Mathematica code illustrates the above expressions.
View Mathematica Code:

M = {{M11, M12}, {M21, M22}}
A = M.M - Tr[M] M + Det[M]*IdentityMatrix[2]
FullSimplify[A]

Three Dimensional Matrices

Consider the matrix:

$M= \left( \begin{array}{ccc} M_{11}&M_{12}& M_{13}\\ M_{21}&M_{22}& M_{23}\\ M_{31}&M_{32}& M_{33} \end{array} \right)$

Therefore, the characteristic equation of $M$ is given by:

$\det{\left(\lambda I - M\right)}=\det{\left( \begin{array}{ccc} \lambda-M_{11}&-M_{12}&-M_{13}\\ -M_{21}&\lambda-M_{22}&-M_{23}\\ -M_{31}&-M_{32}&\lambda-M_{33} \end{array} \right) }=0$

I.e.,

$\det{\left(\lambda I - M\right)} = \lambda^3 - I_1(M)\lambda^2+ I_2(M)\lambda - I_3(M)=0$

The matrix $M$ satisfies the characteristic equation as follows:

$M^3-(I_1(M))M^2+(I_2(M))M-(I_3(M))I=\left( \begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array} \right)$

The above polynomial expressions in the components of the matrix $M$ equate to zero as illustrated using the following Mathematica code:
View Mathematica Code:

M = {{M11, M12,M13}, {M21, M22,M23},{M31, M32,M33}}
I2=1/2*(Tr[M]^2-Tr[M.M]);
A = M.M.M - Tr[M] M.M + I2*M-Det[M]*IdentityMatrix[3]
FullSimplify[A]

One can show using induction that for $M\in\mathbb{M}^3$ , the matrix $M^n$ for $n\geq 3$ can be written as a linear combination of $M^2$ , $M$ , and $I$ such that:

$M^n=f_1M^2+f_2M+f_3I$

where $f_1$ , $f_2$ , and $f_3$ are functions of the invariants $I_1(M)$ , $I_2(M)$ , and $I_3(M)$ .
Similarly, if $M$ is invertible, then, $M^{-n}$ for $n\geq 1$ can be written as: