Engineering Mechanics: STATICS: Introduction
What engineering mechanics is
Mechanics is a branch of physics that deals with the states of bodies under the action of forces. Engineering mechanics implements the principles of mechanics to solve practical problems. Engineering mechanics has the following branches:
- Rigid-body mechanics
- Statics: deals with the equilibrium of non-deforming bodies at rest or moving with constant velocity (no acceleration).
- Dynamics: deals with the motion of non-deforming bodies that have acceleration.
- Deformable-body mechanics: deals with deformations of solid bodies and their internal forces.
- Fluid mechanics: deals with the motion of fluids and their internal forces (pressure or viscous forces).
This course is focused on statics, i.e. mechanics of rigid-bodies at rest.
Fundamental Concepts and Principles
Basic quantities
A physical quantity is a property that can be quantified by measurement. A physical quantity is measured by comparison with a standard. The unit of measurement is a unique name assigned to a measure of a quantity. For example, meter is a unit of length. The standard for length, corresponding to 1.0 unit of meter, can be a piece of metal bar, or the distance traveled by light in a vacuum during a certain fraction of time unit.
One should distinguish between the concepts of dimension and unit being usually confused. A dimension is a physical quantity that can be measured (e.g. length, time, temperature, etc.), whereas a unit is a name correlating with the dimension to make it relative. A dimension can have several units all being related through conversion factors. For example, length is a dimension with meter and foot as two of its units such that 1 meter is 3.28084 feet.
Length, time, and mass are three basis measures or dimensions with the following definitions:
Length. Length is a measure of distance between two points in space. Length is used to measure the relative positions of points in space to a fixed point. Some units of length are meter, inch, foot, yard, etc. The dimension of length is denoted by ![]() .
.
Time. Time is understood as the succession of events. In physics, time is defined by its measurements, i.e. what a clock (a device for measuring time) reads. Some units of time are seconds, minute, hour, day, year, century, etc. The dimension of time is denoted by ![]() .
.
Mass. Mass measures the quantity (how much) of matter. It also measures the resistance of a body to acceleration (change in velocity) when subjected to net force, or measures the gravitational attraction between two bodies. The units of mass are kilogram, pound, slug, etc. The dimension of mass is denoted by ![]() .
.
Other quantities: Generally, the three basic quantities mass, length, and time creates a system of dimensions called the MLT system. There are many other physical quantities that their dimensions are derived based on the above three basic dimensions. For example: area has the dimension of length![]() length being written as
length being written as ![]() . Some others are:
. Some others are:
| Quantity | Dimension |
| Volume | |
| Velocity | |
| Acceleration | |
| Force | |
| Angle |
Force is a quantity perceived by push or pull exerted by one body onto another. Force is related to the basic quantities through the second Newton’s Law. The concept of force will be fully covered in section #.#.
As a remark, an angle is a physical quantity that has no dimension in the MLT system. Why? The reason emerges by noting the definition and measure of an angle. An angle is defined as the figure formed by two rays, i.e. two half-lines sharing a point and starting from that point. The measure of an angle is the ratio of the length of a circular arc made by the angle to its radius. Since both the length of the arc and the length of the radius have the same dimension, their ratio becomes dimensionless. Common units for measuring angles are Radian and degree.
Idealizations
Idealizations or models are simplifications of phenomena so that calculations based on theories and laws become practical.
Particle. A particle is a localized object that have mass but its size can be neglected. This means that the size and geometry of an object regarded as a particle does not significantly affect our calculations. For example, any object (e.g. a car, a cat, the earth) can be simplified into a particle when we study their motion from one location to another.
Rigid body: A rigid body is an object that does not experience deformations when being loaded (e.g. pressed or pulled). The distance between two points on/in a rigid body is always the same, whether or not a force is applied to the object. As a result, the shape of a rigid body does not change. In reality, all objects are deformable; however, a rigid-body idealization is suitable in many problem-solving situations in which the deformations are relatively small.
International System of Units (SI)
A system of unit is a collection of units of measurements. Two common systems of units are the International System of Units (SI) and the U.S. Customary system of units (FPS). The SI is used through this book. The following table shows the SI units of some quantities often used in mechanics:
| Quantity | Unit name | Unit notation |
|---|---|---|
| Length | meter | |
| Time | second | |
| Mass | kilogram | |
| Area | square meter | |
| Volume | cubic meter | |
| Velocity | meter per second | |
| Acceleration | meter per second squared | |
| Density | kilogram per cubic meter | |
| Force | newton |
Numerical Calculations
It is important to consider the following aspects when doing calculations and reporting the answers to engineering problems.
Dimensional Homogeneity
The logic implies that only physical quantities with identical dimensions and units can be added to each other or subtracted from one another. For example it makes sense to add masses of objects, but it is nonsense to add the mass to velocity. Moreover, terms on both sides of an equation should have the same dimension and unit. Multiplication and division of physical quantities with different dimensions and units are logically allowed. It is obvious that all units in the calculations comply with a system of the units chosen in advance.
Rounding Numbers
Rounding a number means replacing the number with a different one being approximately equal to the original number. Rounding can have two proposes:
- Simplifying the number to make it easier to report. For example: 400 is easier and more explicit to report than 398, or the number
 is usually approximated as 3.14.
is usually approximated as 3.14. - Avoiding misleading accuracy when reporting computed or measured quantities. For example, it is not appropriate to report the mass of a person as 61.23453409 kg when measuring with a body weight scale (bathroom scale).
Rounding a number needs a rule or an instruction. It is usually told how to round a number, or it is understood from the context (e.g. the accuracy of the device of the measurements). There are two ways for declaring an instruction of rounding a number.
- Rounding to a named place. For example rounding a number to the nearest tenth, or rounding a number to a specific number of significant digits (see the next section).
- Rounding to a specific number of places. For example rounding a number to four decimal places.
Once the place (target place) that a number should be rounded to is known, the digit one place to the right of the target place is considered. Then, if the place (right to the target place) is 5 or greater, the target digit is rounded up by 1. Otherwise, the target digit is left as it is. The next step is to replace any digits to the right of the target digits with zeros if they are to the left of the decimal point and/or to delete the digits if they are to the right of the decimal point. Calculation tip: use a vertical line, |, to separate the target place from the rest of the digits. The target place falls just before the vertical line.
Example 1: Consider the number 9647:
- 9647 rounded to the nearest ten is 9650 (hint:
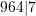 ).
). - 9647 rounded to the nearest hundred is 9600 (hint:
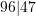 ).
). - 9647 rounded to the nearest thousand 10000 (hint:
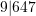 ).
).
Example 2: Consider the number 2.0623:
- 2.0623 rounded to the nearest unit is 2 (hint:
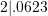 ).
). - 2.0623 rounded to the nearest tenth is 2.1 (hint:
 ).
). - 2.0623 rounded to the nearest hundredth is 2.06 (hint:
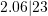 ).
). - 2.0623 rounded to the nearest thousandth 2.062 (hint:
 ).
).
Example 3: Consider the number ![]() :
:
 rounded to to five decimal places is 3.14159 (hint:
rounded to to five decimal places is 3.14159 (hint: 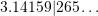 ).
). rounded to to four decimal places is 3.1416 (hint:
rounded to to four decimal places is 3.1416 (hint: 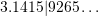 ).
). rounded to to three decimal places is 3.142 (hint:
rounded to to three decimal places is 3.142 (hint:  ).
).
Example 4: Consider the numbers 4.296 and 5.98:
- 4.296 rounded to the nearest hundredth (or two decimal place) is 4.30 (hint:
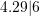 ).
). - 5.98 rounded to the nearest tenth (or one decimal place) is 6.0 (hint:
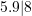 ).
).
In the last example, zeros should be included to indicate the decimal place the numbers are rounded to. It is therefore wrong to write 4.3 and 6 respectively for the above cases.
Significant figures
Significant figures or significant digits of a number are digits that show us the accuracy of a measurement or calculations based on the measurement. Each significant figure adds accuracy to the reported measurement. Since significant figures are to demonstrate the accuracy of measurements, the number of significant figures in a number directly depends on the precision of the measuring instrument. The significant figures of a reported measurement contains the digits that we are reasonable sure of. Usually, the last digit has some uncertainty, but it is reasonable to be reported.
For example, the length of an object measured by a ruler with the accuracy of tenth of centimetre i.e. millimetre can be reported as 2.34 cm. The numbers 2 and 3 are certain because we can observe the marks on the ruler, but, 4 has some uncertainty because we can see the edge of the object ends somewhere between two millimetre marks on the ruler. However, we estimate the last digit on our engineering judgment. Obviously, it does not make sense to report a thousandth place for this measurement (e.g. 2.347), because even the hundredth place is itself uncertain.
As noted in the example, the significant figures include the certain digits and the first uncertain digits out of a measurement. There are some rules to make a digit significant or non-significant. Non-significant digits are placeholder zeros. A placeholder zero is either a trailing zero in a non-decimal number, or a leading zero at the beginning of a decimal number less than 1. Here, are some examples before formally declaring the rules of the significant figures:
Example 1: These measurements have 4 significant figures (3 certain digits and 1 uncertain): 2351, 2002, 21.26, 0.2314, 0.3006
Example 2: These measurements have only 1 significant figures (1 certain digit): 1000, 0.000001. The zeros are just placeholders determining the order of the numbers. The measurements can be written as ![]() and
and ![]() .
.
Example 3: These measurements have 3 significant digits (2 certain digits and 1 uncertain): 0.0000361, 0.0000540, 1.01
Example 4: These measurements have 4 significant digits (3 certain digits and 1 uncertain): 100.0, 541.0, 6520. (note the decimal point after zero; zero is not just a place holder in this case).
Remark: a measurement reported as 100 has only 1 significant figure, but a measurement reported as 100.0 has 4 significant figures. The zero after the decimal point in 100.0 tells us that the measurement was accurate to the tenths place; it happened to be zero in this case.
Example 5: These examples shows how to indicate the accuracy to a certain place:
7 is accurate to the units place (1 significant figure).
1007 is accurate to the units place (4 significant figures).
770. is accurate to the units place (note the decimal point).
10 is accurate to the tens place (1 significant figure).
770 is accurate to the tens place (2 significant figures).
700 is accurate to the hundreds place (1 significant figure).
1000.0 is accurate to the tenths place (5 significant figures).
450.0 is accurate to the tenths place (4 significant figures).
3.14159 is accurate to the hundred-thousandths place.
0.00023 is accurate to the hundred-thousandths place.
0.000230 is accurate to the millionths place (note the extra zero).
The rules for significant figures are:
- All nonzero digits are significant.
- All zeroes embedded between significant digits are significant.
- Leading zeros are NOT significant.
- Trailing zeros of a non-decimal number are NOT significant.
Now that the concept of the significant figures is clear, we can round numbers to specific number of significant digits. The method is the same as discussed for rounding a number to a named place.
Example 1: 356892 rounded to 4 significant digits is 356900.
Example 2: 0.08274 rounded to 2 significant digits is 0.083.
Example 3: 120.82 rounded to 4 significant digits is 120.8.
Example 4: 100.82 rounded to 2 significant digits is 10. (note the decimal point after zero).
Reporting the results
The result of a calculation should be rounded as instructed and reported along with its unit. Example:
- Wrong: The reaction force is 2.0.
- Right: The reaction force is 2.0 N.
Recommendations:
Use a decimal point or a decimal point and zeros to indicate the accuracy whenever is applicable. For example 2.00 m, 100. N.
Use engineering notation to report numbers having leading or trailing zeros. For example: write ![]() as
as ![]() , or
, or ![]() as
as ![]() .
.
