Engineering at Alberta Courses

Forces and moments: Forces

In general, force is perceived as push or pull. Forces arise from different sources/causes like gravity, contact forces between bodies, pressure force by fluids on surface of solids, friction forces, electrostatic forces on charged particles, etc.

Physically, force has a magnitude and a direction in the space, and therefore, it is a vector quantity called the force vector. In this regard, the terms force and force vector are equivalent.

The magnitude of a force vector has the dimension $\frac{\text{mass}\cdot \text{length}}{\text{time}^2}$ and the SI unit of Newton denoted by $\rm N$ being equal to $\frac{\text{kg}\cdot \text{m}}{\text{s}^2}$ (please see chapter 1). The direction of a force vector is expressed using a unit vector. This unit vector shows the direction in the (geometrical) space. We can have a graphical representation of a force vector. This graphical representation is by means of an arrow as discussed in chapter 2. The length of an arrow representing the a force vector is arbitrary; however, if there is a set of forces to be geometrically (graphically) represented, they have to be drawn proportionately or with some scale. For example, a force vector of magnitude $10\ \rm{ N}$ should be at least drawn smaller than a force vector of magnitude $200\ \rm N$ if not drawn proportionately.

Denoting a force vector with $\bold F$ , we can write:

(1) $\bold F=F\bold u_F$

where $F=\vert \bold F\vert$ and $\bold u_F$ is a unit vector expressing the direction of $\bold F$ . Note that $F$ has the unit of Newton, and the unit vector has no dimension and unit. Equation 1 readily implies that:

(2) $\bold u_F = \frac{\bold F}{F}$

Line of action of a force. The line of action of a force or a force vector $\bold F$ is a line that is colinear with the force vector (arrow representing the force). In other word, this line is colinear with $\bold u_F$ . The line of action and the unit vector are geometrical objects.

Setting a Cartesian frame, any force vector $\bold F$ can be resolved into their Cartesian components using the CVN:

(3) $\bold F = F_x\bold i + F_y\bold j + F_z\bold k$

where $(F_x,F_y,F_z)$ are the scalar components each having the dimension and unit of force. A graphical representation of $\bold F$ in the cartesian frame is shown in Figure 2. It should be noted that the $x$ , $y$ and $z$ axes have the unit of force (no length).

Figure 1. A graphical representation of a force vector and its components (rectangular and scalar) in a Cartesian frame.

A force vector, unlike a general vector, conveys a physical phenomenon. We say a body is subjected to a force (or a system of forces), or a force acts on a body. This expresses the fact that a force (or a system of forces) is acting or exerted at a particular location (or locations) of the body. This is a natural perception that pulling on one’s arm is different from pulling on one’s leg. Therefore, the location at which a force vector is acting is deterministically important and not arbitrary. A force vector, by its nature, acts at a point. This is graphically demonstrated by drawing the force vector with its tail or head touching the point at which the force acts (Figure 1). Depending on the tail or the head of the vector touching the point, this representation may also imply a sense of pull or push by the force (Figure 1). The sense of pull or push is not important in many problems (for example rigid body equilibrium problems), but, only the force vector and the point at which the force is acting become important in the calculations. As a tangible example, the a sense of pull or push is not involve in finding the acceleration of an object using the Newton’s second law.

Figure 2. Graphical representations of forces acting at points of an object.

Concentrated force. In reality, forces are in the form of loads. Load is a set of forces distributed over an area of a body. For example, we perceive and feel that the ground reaction force is distributed on the soles of our feet; we do not feel a sharp feeling of a force there. In fact, all force in nature are distributed, and there is no force concentrated at or acting on a point (a mathematical notion with no dimension). However, we idealize or approximate a load by a concentrated force being represented by a force vector and shown by an arrow. This idealization is performed when the area on which the load is distributed is relatively small compared to the size of the body. Moreover, the effects of loads or distributed forces are manifested by equivalent concentrated forces in the problems in which the overall effect of the load on the whole body is important, not the local effects.

System of forces. A system of forces or a force system is referred to a discrete set of forces exerted on a body (object, structure, etc)

Remark: since a force vector is represented by an arrow (vector), all calculations related to forces are done based on the vector operations explained in chapter 2.

Resultant force

Let $\bold F_1, \bold F_2\dots ,\bold F_n$ be a system of $n$ forces (set of forces), their resultant or the resultant force $\bold F_R$ is the vector sum over the forces:

(3) $\bold F_R = \bold F_1 + \bold F_2 + \dots + \bold F_n=\sum_{i=1}^n\bold F_i$

which can be expanded to summing over the components using the CVN:

$\bold F_R = \sum \bold F= \sum F_x\bold i + \sum F_y\bold j+\sum F_z\bold k\tag {4}$

Remark: the forces (force vectors) should become concurrent before applying the vector operations.

Example

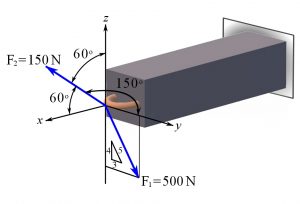
— to be added–

Force directed along a line

A force vector has a line of action being colinear with the force vector and indeed with the unit vector specifying the direction of the force. In many problems, the force is directed along a line-shape physical object or structure like a cable or a bar. In such a case, the line of action of the force is colinear with the physical shape of the structure (Figure 3). Therefore, the unit vector expressing the direction of the force can be obtained through finding a colinear vector (arrow) with the line of action or the structure. To do this, we initially set or consider the given a Cartesian coordinate system. Choosing a point as the coordinate system origin, if not given, is arbitrary, however, we should try to wisely choose a point that will facilitate the calculations. Then, two points, say $A$ and $B$ , on the line of action or the structure are considered. These are points with known coordinates or points that their coordinates are easy enough to calculate (Figure 3). Considering the position vectors of $A$ and $B$ , we find the (displacement) vector $\bold r_{AB}$ as:

$\bold r_{AB}=\bold r_B-\bold r_A=(x_B-x_A)\bold i+(y_B-y_A)\bold j+(z_B-z_A)\bold k$

The unit vector $\bold u_F$ is obtained by normalizing $\bold r_{AB}$ by its magnitude (length), $\bold u_F=\frac{\bold r_{AB}}{r_{AB}}$ . Consequently, the force vector $\bold F$ can be written as:

(5) $\bold F=F\bold u_F=F(\frac{\bold r_{AB}}{r_{AB}})=F(\frac{\bold (x_B-x_A)\bold i+(y_B-y_A)\bold j+(z_B-z_A)\bold k}{\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}})$

As shown in Figure 3, the graphical representation of $\bold F$ , $\bold r_{AB}$ and $\bold u_{AB}$ are colinear. Note that $\bold F$ has the dimension of force, $\bold r_{AB}$ has the dimension of length, and the unit vector $\bold u_F$ has no dimension. Despite having different dimensions and units, all vectors can be graphically shown in one figure.

Figure 3. Obtaining the force vector of a force directed along a line.