Engineering at Alberta Courses » The Velocity Gradient

Displacement and Strain: The Velocity Gradient

The Velocity Gradient is a spacial tensor that carries the information on the velocity of vectors in the deformed configuration when an object is being deformed as a function of time. Let $X\in \Omega_0\subset\mathbb{R}^3$ describe the position in the reference configuration and $x\in\Omega\subset\mathbb{R}^3$ describe the instantaneous position in the deformed configuration. The velocity field of the deformed configuration is described by $v=\dot{x}=\frac{\partial x}{\partial t}\in\mathbb{R}^3$ . Let $dx$ be a vector in the deformed configuration, being the image of a vector $dX$ in the reference configuration. Then, the rate of change of $dx$ with respect to time, namely $\dot{dx}$ is given by:

$\dot{dx}=\dot{F}dX$

The relationship between the vectors $dx=FdX$ , can be used to replace $dX$ as follows:

$\dot{dx}=\dot{F}F^{-1}dx$

That way, the vector $\dot{dx}$ is a function of the vector $dx$ . The tensor $L=\dot{F}F^{-1}$ is termed the velocity gradient since it is the gradient of the vector field $v$ as follows.

$L=\dot{F}F^{-1}=\frac{\partial^2 x}{\partial X \partial t}\frac{\partial X}{\partial x}=\frac{\partial v}{\partial X }\frac{\partial X}{\partial x}=\frac{\partial v}{\partial x}$

In component form, the velocity gradient has the form:

$L_{ij}=\frac{\partial v_i}{\partial x_j}$

The stretching tensor $D$ is defined as the symmetric part of $L$ while the spin tensor $W$ is defined as the skewsymmetric part of $L$ :

$D=\frac{1}{2}(L+L^T)\qquad W=\frac{1}{2}(L-L^T)$

Behaviour under Rigid Body Rotation:

The stretching tensor is a true measure of the instantaneous deformation of an object. Assuming that a body is moving in space with a rigid body rotation $Q$ , i.e.:

$x=QX$

Then, the velocity gradient is equal to:

$L=\dot{Q}Q^T$

The stretching and spin tensors have the following forms:

$D=\frac{1}{2}(\dot{Q}Q^T+Q\dot{Q}^T)\qquad W=\frac{1}{2}(\dot{Q}Q^T-Q\dot{Q}^T)$

However, the rotation matrix satisfies the following relationships:

$I=QQ^T\qquad 0=\dot{I}=\dot{Q}Q^T+Q\dot{Q}^T$

Therefore:

$D=0\qquad W=L$

Local Change in Volume and the Velocity Gradient

An important relationship that is used throughout the derivations in continuum mechanics is the relationship between the trace of the velocity gradient, namely $\mbox{Trace}(L)$ and the determinant of the deformation gradient $\det F$ . Denoting $J=\det F$ , the relationship is given as follows:

$\dot{J} = J \mbox{Trace}(L)$

There are two ways to show the above relationship. The first relies on expressing each side in terms of their components and is adopted from the book by Ogden. $J$ can be expressed in terms of the components of $F$ as follows:

$J=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}$

Then, by taking the time derivatives:

$\dot{J} = \sum_{i,j,k=1}^3\varepsilon_{ijk}\left(\frac{\partial \dot{x_1}}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial x_1}{\partial X_i}\frac{\partial \dot{x_2}}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial \dot{x_3}}{\partial X_k}\right)$

The following relationship is first used to replace the expressions $\frac{\partial \dot{x_k}}{\partial X_l}$ with the velocity gradient components:

$\frac{\partial \dot{x_k}}{\partial X_l}=\sum_{i=1}^3\frac{\partial \dot{x_k}}{\partial x_i}\frac{\partial x_i}{\partial X_l}$

From the properties of the determinant, the following expressions are equal to zero for any values of $a,b\leq 3$ :

$\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_a}{\partial X_j}\frac{\partial x_b}{\partial X_k}=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_b}{\partial X_j}\frac{\partial x_b}{\partial X_k}=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_b}{\partial X_j}\frac{\partial x_a}{\partial X_k}=0$

Which results in the following:

$\begin{split} \dot{J} & = \sum_{i,j,k=1}^3\varepsilon_{ijk}\left(\frac{\partial \dot{x}_1}{\partial x_1}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial \dot{x}_2}{\partial x_2}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial \dot{x}_3}{\partial x_3}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}\right)\\ &=J\mbox{Trace}(L) \end{split}$

Another proof is adopted from the book by P. Chadwick and relies on the expressions shown in the matrix invariants section. Let $a,b,c\in\mathbb{R}^3$ be three linearly independent vectors. $\dot{J}$ can be expressed as follows:

$\begin{split} \dot{J} &=\frac{\dot{F}a\cdot(Fb\times Fc)+Fa\cdot(\dot{F}b\times Fc)+Fa\cdot(Fb\times \dot{F}c)}{a\cdot(b\times c)}\\ &=\frac{\dot{F}F^{-1}Fa\cdot(Fb\times Fc)+Fa\cdot(\dot{F}F^{-1}Fb\times Fc)+Fa\cdot(Fb\times \dot{F}F^{-1}Fc)}{a\cdot(b\times c)}\\ &=\frac{\dot{F}F^{-1}Fa\cdot(Fb\times Fc)+Fa\cdot(\dot{F}F^{-1}Fb\times Fc)+Fa\cdot(Fb\times \dot{F}F^{-1}Fc)}{Fa\cdot(Fb\times Fc)}\frac{Fa\cdot(Fb\times Fc)}{a\cdot(b\times c)}\\ &=J \mbox{Trace}(\dot{F}F^{-1})\\ &=J \mbox{Trace}(L) \end{split}$

The above relationship implies that if a deformation is associated with a zero change in volume, i.e., $\det(F)=J=1$ and $\dot{J}=0$ , then this is associated with a zero trace of the velocity gradient. i.e., for an isochoric motion:

$\dot{J}=J \mbox{Trace}(L)=\left(\frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3}\right)=0$

Examples and Problems:

Problems:

Consider the two dimensional position function:
$\begin{split} x_1&=X_1+X_2t\\ x_2&=X_2+X_1\frac{t}{2} \end{split}$

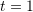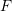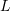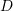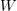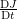Evaluate the following at $t=1$ : $F$ , $L$ , $D$ , $W$ , and $\frac{\mathrm{D}J}{\mathrm{D}t}$ . Also, find 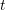$t$ at which the above relationship will stop being physically possible.
Find the stretch and spin tensors of the deformation described by:
$x=\left(\begin{matrix}\lambda_1(t)&0&0\\0&\lambda_2(t)&0\\0&0&\lambda_3(t)\end{matrix}\right)\left(\begin{array}{c}X_1\\X_2\\X_3\end{array}\right)$