Linear Maps between vector spaces: Additional Definitions and Properties of Linear Maps
Matrix Transpose
Let ![]() be a linear map. If
be a linear map. If ![]() is the matrix representation after choosing particular orthonormal basis sets for the underlying spaces, then, the transpose of
is the matrix representation after choosing particular orthonormal basis sets for the underlying spaces, then, the transpose of ![]() or
or ![]() , is a map
, is a map ![]() whose columns are the rows of
whose columns are the rows of ![]() .
.
In component form, this means:
![]()
The above definition relies on components. Another equivalent but more convenient definition is as follows.
Let ![]() be a linear map. Then,
be a linear map. Then, ![]() is the unique linear map that satisfies:
is the unique linear map that satisfies:
![]()
Any of the above two definitions can be used to show the following facts about the transpose of square matrices. ![]()
![]()
Notice that since the determinant of a square matrix ![]() is the same whether we consider the rows or the columns, then:
is the same whether we consider the rows or the columns, then:
![]()
For example
![Rendered by QuickLaTeX.com \[ A= \left( \begin{array}{ccc} 1&9&3\\ 2&9&5 \end{array} \right) \hspace{10mm} \Rightarrow \hspace{10mm} A^T= \left( \begin{array}{cc} 1&2\\ 9&9\\ 3&5 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-930d72b047c0da6144ac2b87a15b60d4_l3.png)
![Rendered by QuickLaTeX.com \[ B= \left( \begin{array}{ccc} 1&9&2\\ 4&1&3\\ 5&2&7 \end{array} \right) \Rightarrow \det(B)=-110 \hspace{10mm} B^T= \left( \begin{array}{ccc} 1&4&5\\ 9&1&2\\ 2&3&7 \end{array} \right) \Rightarrow \det(B^T)=-110 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c1f8d078de06499edf6774d1a8e9eca0_l3.png)
Matrix Inverse
Let ![]() be a linear map. The following are all equivalent:
be a linear map. The following are all equivalent:
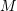 is invertible
is invertible- The rows of the matrix representation of
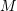 are linearly independent
are linearly independent - The kernel of the
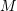 contains only the zero vector
contains only the zero vector 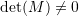
In this case, the inverse of ![]() is denoted
is denoted ![]() and satisfies:
and satisfies:
![]()
Notice that ![]() is unique, because if there is another matrix
is unique, because if there is another matrix ![]() such that
such that ![]() , then
, then ![]() .
.
Notice also that if ![]() such that
such that ![]() and
and ![]() , then,
, then, ![]() .
.
If the linear maps ![]() and
and ![]() are invertible, then it is easy to show that
are invertible, then it is easy to show that ![]() is also invertible and:
is also invertible and:
![]()
Matrix Inverse in 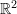
Consider the matrix:
![]()
Then, the inverse of ![]() can be shown to be:
can be shown to be:
![]()
Try it out, input the values of the matrix ![]() and press evaluate to calculate its inverse.
and press evaluate to calculate its inverse.
Matrix Inverse in 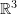
Consider the matrix:
![Rendered by QuickLaTeX.com \[ M=\left( \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c1a3c059fcb95b822e83aa9dd4985fc5_l3.png)
If ![]() ,
, ![]() and
and ![]() , then, the inverse of
, then, the inverse of ![]() can be shown to be:
can be shown to be:
![Rendered by QuickLaTeX.com \[ M^{-1}={1\over (a\cdot (b \times c))}\left( \begin{array}{ccc} \vdots&\vdots&\vdots\\ b\times c&c\times a & a \times b\\ \vdots&\vdots&\vdots \end{array} \right) ={1\over \det(M)}\left( \begin{array}{ccc} \vdots&\vdots&\vdots\\ b\times c&c\times a & a \times b\\ \vdots&\vdots&\vdots \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f4b7126222845d2885a987426065278e_l3.png)
Try it out, input the values of the matrix ![]() and press evaluate to calculate its inverse.
and press evaluate to calculate its inverse.
Invariants
Consider ![]() with the two orthonormal basis sets
with the two orthonormal basis sets ![]() and
and ![]() with a coordinate transformation matrix
with a coordinate transformation matrix ![]() such that
such that ![]() .
.
Clearly, the components of vectors and the matrices representing linear operators change according to the chosen coordinate system (basis set). Invariants are functions of these components that do not change whether ![]() or
or ![]() is chosen as the basis set.
is chosen as the basis set.
The invariants usually rely on the fact that ![]() .
.
Vector Invariants
Vector Norm
A vector ![]() has the representation
has the representation ![]() with components
with components ![]() when
when ![]() is the basis set. Alternatively, it has the representation
is the basis set. Alternatively, it has the representation ![]() with components
with components ![]() when
when ![]() is the basis set.
is the basis set.
The norm of the vector ![]() is an invariant since it is equal whether we use
is an invariant since it is equal whether we use ![]() or
or ![]() .
.
The norm of ![]() when
when ![]() is the basis set:
is the basis set:
![]()
The norm of ![]() is also equal to the norm of
is also equal to the norm of ![]() :
:
![]()
Vector Dot Product
Similarly, the dot product between two vectors ![]() is invariant:
is invariant:
![]()
Matrix Invariants in 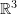
We will restrict our discusion of invariants when the underlying space is ![]() . A linear operator
. A linear operator ![]() has the matrix representation
has the matrix representation ![]() with components
with components ![]() when
when ![]() is the basis set.
is the basis set.
Alternatively, it has the representation ![]() with components
with components ![]() when
when ![]() is the basis set. The following are some invariants of the matrix
is the basis set. The following are some invariants of the matrix ![]() :
:
First Invariant, Trace
The trace of ![]() or
or ![]() is defined as:
is defined as:
![]()
![]() is invariant for if we consider the components in
is invariant for if we consider the components in ![]() :
:
![Rendered by QuickLaTeX.com \[ I_1(M')=\sum_{i=1}^3M'_{ii}=\sum_{i,j,k=1}^3Q_{ij}M_{jk}Q_{ik}=\sum_{j,k=1}^3\delta_{jk}M_{jk}=\sum_{j=1}^3M_{jj}=I_1(M) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-10d48b429d424f1015694b7ff34f1c07_l3.png)
It is straight forward from the definition to show that ![]() :
:
![]()
The above definition for the first invariant depends on the components in a given coordinate system. Another definition according to P. Chadwick that is independent of a coordinate system is given as follows:
![Rendered by QuickLaTeX.com \[ \begin{split} I_1(M)&=Me_1\cdot e_1+Me_2\cdot e_2+Me_3\cdot e_3\\ &=Me_1\cdot (e_2\times e_3)+e_1\cdot (Me_2\times e_3)+e_1\cdot (e_2\times Me_3)\\ &=\frac{Ma\cdot (b\times c)+a\cdot (Mb\times c)+a\cdot (b\times Mc)}{a\cdot(b\times c)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ad0d2fba96613744818c672be41b53ab_l3.png)
where, ![]() and
and ![]() are three arbitrary linearly independent vectors. Use the components of
are three arbitrary linearly independent vectors. Use the components of ![]() and
and ![]() to verify that the two definitions are equivalent.
to verify that the two definitions are equivalent.
Second Invariant
The second invariant ![]() is defined as:
is defined as:
![]()
Clearly, since ![]() is invariant, so is
is invariant, so is ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} I_2(M')&={1\over 2}(\left(I_1(M')\right)^2-I_1(M'M'))={1\over 2}(\left(I_1(QMQ^T)\right)^2-I_1(QMMQ^T)\\ &={1\over 2}(\left(I_1(M)\right)^2-I_1(MM)\\ &=I_2(M) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1a22e03ee9ebfd430c4cc0a879d4d1b2_l3.png)
Another definition for the second invariant according to P. Chadwick that is independent of a coordinate system is given as follows:
![Rendered by QuickLaTeX.com \[ \begin{split} I_2(M)&=Me_1\cdot (Me_2\times e_3)+Me_1\cdot (e_2\times Me_3)+e_1\cdot (Me_2\times Me_3)\\ &=\frac{Ma\cdot (Mb\times c)+Ma\cdot (b\times Mc)+a\cdot (Mb\times Mc)}{a\cdot(b\times c)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7ef59f487bd5879eea148ca553de0cb3_l3.png)
where, ![]() and
and ![]() are three arbitrary linearly independent vectors. Use the components of
are three arbitrary linearly independent vectors. Use the components of ![]() and
and ![]() to verify that the two definitions are equivalent.
to verify that the two definitions are equivalent.
Third Invariant, the Determinant
The third invariant ![]() is defined as the determinant of the matrix
is defined as the determinant of the matrix ![]() ;
;
![]()
Clearly, ![]() is invariant:
is invariant:
![]()
Another definition for the third invariant according to P. Chadwick that is independent of a coordinate system is given as follows:
![Rendered by QuickLaTeX.com \[ \begin{split} I_3(M)&=Me_1\cdot (Me_2\times Me_3)\\ &=\frac{Ma\cdot (Mb\times Mc)}{a\cdot(b\times c)} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4b035124ceabe0d6d54577e89d51db3c_l3.png)
where, ![]() and
and ![]() are three arbitrary linearly independent vectors. Use the components of
are three arbitrary linearly independent vectors. Use the components of ![]() and
and ![]() to verify that the two definitions are equivalent.
to verify that the two definitions are equivalent.
The trace (first invariant) and determinant (third invariant) of a matrix ![]() are related as follows:
are related as follows:
![]()
Eigenvalues are Invariants
The eigenvalues of the matrices ![]() and
and ![]() are the same (why?).
are the same (why?).
It is worth mentioning that the three invariants mentioned above appear naturally in the characteristic equation of ![]() :
:
![]()
Input the components of a matrix ![]() in the following tool and three angles for coordinate transformation. The tool then calculates the three matrix invariants along with the eigenvalues and eigenvectors in both coordinate systems. As expected, the invariants and the eigenvalues are the same. However, the components of the eigenvectors are different. The vectors themselves are the same, but the components are different according to the relationship
in the following tool and three angles for coordinate transformation. The tool then calculates the three matrix invariants along with the eigenvalues and eigenvectors in both coordinate systems. As expected, the invariants and the eigenvalues are the same. However, the components of the eigenvectors are different. The vectors themselves are the same, but the components are different according to the relationship ![]() .
.
Cayley-Hamilton Theorem
The Cayley-Hamilton Theorem is an important theorem in linear algebra that asserts that a matrix satisfies its characteristic equation. In other words, let ![]() . The eigenvalues of
. The eigenvalues of ![]() are those that satisfy:
are those that satisfy:
![]()
where ![]() are polynomial expressions of the entries of the matrix
are polynomial expressions of the entries of the matrix ![]() . In particular,
. In particular, ![]() . Then, the Cayley-Hamilton Theorem asserts that:
. Then, the Cayley-Hamilton Theorem asserts that:
![]()
The first equation is a scalar equation which is a polynomial expression of the variable ![]() . However, the second equation is a matrix equation in which the sum of the given matrices gives the 0 matrix. Without attempting a formal proof for the theorem, in the following we will show how the theorem applies to
. However, the second equation is a matrix equation in which the sum of the given matrices gives the 0 matrix. Without attempting a formal proof for the theorem, in the following we will show how the theorem applies to ![]() and
and ![]() .
.
Two Dimensional Matrices
Consider the matrix:
![]()
Therefore, the characteristic equation of ![]() is given by:
is given by:
![]()
I.e.,
![Rendered by QuickLaTeX.com \[ \begin{split} \det{\left(\lambda I - M\right)} &= \lambda^2 - \left(M_{11}+M_{22}\right)\lambda + \left(M_{11}M_{22}-M_{12}M_{21}\right)\\ &=\lambda^2-\text{Tr}(M)\lambda+\det{M}\\ &=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4253891d47de95a46b75039f8083c305_l3.png)
The matrix ![]() satisfies the characteristic equation as follows:
satisfies the characteristic equation as follows:
![]()
Where:
![]()
![]()
and
![]()
The following Mathematica code illustrates the above expressions.
View Mathematica Code:
M = {{M11, M12}, {M21, M22}}
A = M.M - Tr[M] M + Det[M]*IdentityMatrix[2]
FullSimplify[A]
Three Dimensional Matrices
Consider the matrix:
![Rendered by QuickLaTeX.com \[ M= \left( \begin{array}{ccc} M_{11}&M_{12}& M_{13}\\ M_{21}&M_{22}& M_{23}\\ M_{31}&M_{32}& M_{33} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7557d5af6f1c12aac955584b86b05e0c_l3.png)
Therefore, the characteristic equation of ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[ \det{\left(\lambda I - M\right)}=\det{\left( \begin{array}{ccc} \lambda-M_{11}&-M_{12}&-M_{13}\\ -M_{21}&\lambda-M_{22}&-M_{23}\\ -M_{31}&-M_{32}&\lambda-M_{33} \end{array} \right) }=0 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fccbac99b55a3575c7517642766f6a25_l3.png)
I.e.,
![]()
The matrix ![]() satisfies the characteristic equation as follows:
satisfies the characteristic equation as follows:
![Rendered by QuickLaTeX.com \[ M^3-(I_1(M))M^2+(I_2(M))M-(I_3(M))I=\left( \begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9170008cb3cb65bd7738ba13c27c8601_l3.png)
The above polynomial expressions in the components of the matrix ![]() equate to zero as illustrated using the following Mathematica code:
equate to zero as illustrated using the following Mathematica code:
View Mathematica Code:
M = {{M11, M12,M13}, {M21, M22,M23},{M31, M32,M33}}
I2=1/2*(Tr[M]^2-Tr[M.M]);
A = M.M.M - Tr[M] M.M + I2*M-Det[M]*IdentityMatrix[3]
FullSimplify[A]
One can show using induction that for ![]() , the matrix
, the matrix ![]() for
for ![]() can be written as a linear combination of
can be written as a linear combination of ![]() ,
, ![]() , and
, and ![]() such that:
such that:
![]()
where ![]() ,
, ![]() , and
, and ![]() are functions of the invariants
are functions of the invariants ![]() ,
, ![]() , and
, and ![]() .
.
Similarly, if ![]() is invertible, then,
is invertible, then, ![]() for
for ![]() can be written as:
can be written as:
![]()
where ![]() ,
, ![]() , and
, and ![]() are functions of the invariants
are functions of the invariants ![]() ,
, ![]() , and
, and ![]() .
.
