Approximate Methods: Point Collocation Method
The statement of the equilibrium equations applied to a set ![]() is as follows. Assuming that at equilibrium
is as follows. Assuming that at equilibrium ![]() is the symmetric Cauchy stress distribution on
is the symmetric Cauchy stress distribution on ![]() and that
and that ![]() is the displacement vector distribution and knowing the relationship
is the displacement vector distribution and knowing the relationship ![]() , then the equilibrium equation seeks to find
, then the equilibrium equation seeks to find ![]() such that the associated
such that the associated ![]() satisfies the equation:
satisfies the equation:
![]()
where ![]() is the body forces vector distribution on
is the body forces vector distribution on ![]() ,
, ![]() is the mass density, and
is the mass density, and ![]() is the space of all possible displacement functions applied to
is the space of all possible displacement functions applied to ![]() , i.e.,
, i.e., ![]() . The term “Kinematically admissible” in
. The term “Kinematically admissible” in ![]() indicates that the space of possible solutions must satisfy the boundary conditions imposed on
indicates that the space of possible solutions must satisfy the boundary conditions imposed on ![]() (as stated below) and any differentiability constraints.
(as stated below) and any differentiability constraints.
The boundary conditions for the equations of equilibrium are usually given on two parts of the boundary of ![]() denoted
denoted ![]() . On the first part,
. On the first part, ![]() , the external traction vectors
, the external traction vectors ![]() are known so we have the boundary conditions for
are known so we have the boundary conditions for ![]() since
since ![]() (
(![]() is the normal vector to the boundary). On the second part,
is the normal vector to the boundary). On the second part, ![]() , the displacement is given.
, the displacement is given.
The point collocation method seeks an approximate solution to the above problem by assuming that the solution ![]() has a particular form with a finite number of unknowns, i.e., by looking for
has a particular form with a finite number of unknowns, i.e., by looking for ![]() in a subset
in a subset ![]() that is finite dimensional but still able to approximate functions in
that is finite dimensional but still able to approximate functions in ![]() . The finite number of unknowns can be found by satisfying the differential equation of equilibrium at a number of chosen points equal to the number of unknowns.
. The finite number of unknowns can be found by satisfying the differential equation of equilibrium at a number of chosen points equal to the number of unknowns.
Example
Using a polynomial function of the third degree, find the displacement function of the shown bar by satisfying the essential boundary conditions, the differential equation of equilibrium at ![]() and at
and at ![]() ., and the nonessential boundary condition at
., and the nonessential boundary condition at ![]() . Assume that the bar is linear elastic with Young’s modulus
. Assume that the bar is linear elastic with Young’s modulus ![]() and cross-sectional area
and cross-sectional area ![]() and that the small strain tensor is the appropriate measure of strain. Ignore the effect of Poisson’s ratio.
and that the small strain tensor is the appropriate measure of strain. Ignore the effect of Poisson’s ratio.
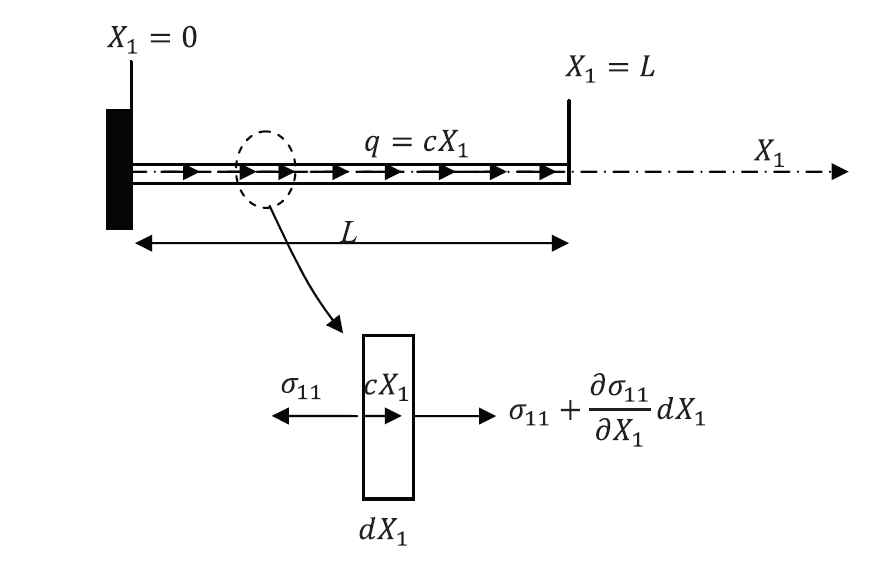
Solution
Exact Solution
The exact solution can be obtained by directly solving the differential equation of equilibrium utilizing ![]() :
:
![]()
with the boundary conditions: ![]() and
and ![]() .
.
Therefore:
![]()
DSolve[{u''[X1] == -c*X1/EA, u'[L] == 0, u[0] == 0}, u[X1], X1]
Approximate Solution
A polynomial of the third degree approximate solution has the form:
![]()
with
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\mathrm{d}u_{approx}}{\mathrm{d}X_1}&=a_1+2a_2X_1+3a_3X_1^2\\ \frac{\mathrm{d}^2u_{approx}}{\mathrm{d}X_1^2}&=2a_2+6a_3X_1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1a22992fa3e34263cf4a6b4e79be7521_l3.png)
The following four equations will be utilized to find the four unknowns:
![Rendered by QuickLaTeX.com \[\begin{split} @X_1=0&:u_{approx}=0\\ @X_1=L&:\frac{\mathrm{d}u_{approx}}{\mathrm{d}X_1}=0\\ @X_1=\frac{L}{2}&:\frac{\mathrm{d}^2u_{approx}}{\mathrm{d}X_1^2}\bigg|_{X_1=\frac{L}{2}}=-\frac{cX_1}{EA}\bigg|_{X_1=\frac{L}{2}}\\ @X_1=L&:\frac{\mathrm{d}^2u_{approx}}{\mathrm{d}X_1^2}\bigg|_{X_1=L}=-\frac{cX_1}{EA}\bigg|_{X_1=L} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a71f9ee3c68f6de8e689e9bfe5dee510_l3.png)
The approximate solution that satisfies the above four unknowns has the form:
![]()
Notice that since the exact solution is contained in the space of approximate functions which were chosen to satisfy both the essential and nonessential boundary conditions, the solution obtained is indeed the exact solution!
View Mathematica Code
u = a0 + a1*x1 + a2*x1^2 + a3*x1^3;
ux = D[u, x1]
uxx = D[ux, x1]
Eq1 = (uxx + c*x1/EA) /. x1 -> L/2;
Eq2 = (uxx + c*x1/EA) /. x1 -> L;
Eq3 = (ux) /. x1 -> L;
Eq4 = u /. x1 -> 0;
s = Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0, Eq4 == 0}, {a1, a2, a3, a0}]
u /. s[[1]]
